समान्तर चतुर्भुज ABCD के विकर्ण एक-दूसरे को बिन्दु 'O' पर काटते है। बिन्दु 'O' से होकर जाने वाली एक रेखा AB को बिन्दु X और CD को बिन्दु Y पर मिलती है। सिद्ध कीजिए कि
AXYD का क्षेत्रफल का क्षेत्रफल
हम जानते है कि समान्तर चतुर्भुज का विकर्ण इसे दो बराबर क्षेत्रफलों के त्रिभुजों में विभक्त करता है।
अब AC समान्तर चतुर्भुज ABCD का विकर्ण है।
का क्षेत्रफल = का क्षेत्रफल
और में,

AO = CO (समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते है) ltrgt (शीर्षाभिमुख कोण)
(एकान्तर अन्तः कोण)
का क्षेत्रफल का क्षेत्रफल
अब का क्षेत्रफल का क्षेत्रफल का क्षेत्रफल
का क्षेत्रफल का क्षेत्रफल [समीकरण (2) से]
का क्षेत्रफल lt
समीकरण (1) से
का क्षेत्रफल का क्षेत्रफल
Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली
27 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.1
1 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
एक समान्तर चतुर्भुज का आधार, संगत शीर्षलम्ब का 3 गुना है। यदि समान्तर चतुर्भुज का क्षेत्रफल 48 वर्ग सेमी है, तो समान्तर चतुर्भुज का आधार और संगत शीर्षफ़ल ज्ञात कीजिए।
View Solutionनिम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित है? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
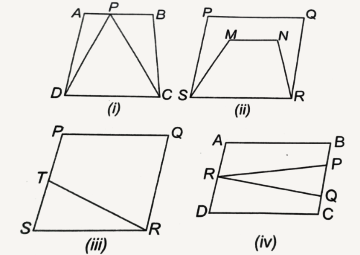
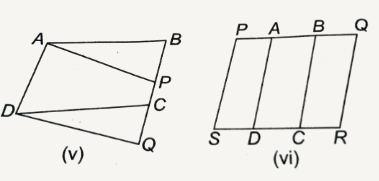
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionबिन्दु (1,0,0) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
View Solutionएक रेखा के कार्तीय समीकरण 6x−2=3y+1=2z−2 है। रेखा के दिक्-अनुपात ज्ञात कीजिए तथा बिन्दु (2,−1,−1) से गुजरने वाली उस रेखा का सदिश समीकरण लिखिए जो दी हुई रेखा के समान्तर है।
View Solutionयदि बिन्दु (a,b),(a',b') और (a−a',b−b') संरेख हो तो सिद्ध कीजिए कि
ab'=a'b.
साथ ही यह भी सिद्ध कीजिए कि इन बिन्दुओं से होकर जाने वाली रेखा मुलबिन्दु से होकर जाती है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionबिन्दु(1,2,3) से जाने वाली तथा रेखा x−42=y+1−3=z+108 के समान्तर रेखा का समीकरण है -
View Solutionबिन्दु (-1,0) से होकर जाने वाले और y-अक्ष को (0,2) पर स्पर्श करने वाला वृत्त निम्न बिन्दु से भी होकर जाता है ।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solution
