ABCD एक आयत है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
माना ABCD एक आयत है जिसकी भुजाओं AB,BC,CD और DA के मध्य बिंदु क्रमशः P,Q,R और S है।
आयत विकर्ण AC को मिलाया।
ΔBAC में P और Q क्रमशः BA और BC के मध्य बिंदु है।
∴PQ∣∣AC और PQ=12AC………..1
ΔADC में
R और S क्रमशः DC और DA के मध्य बिंदु है।
∴SR∣∣AC और SR=12AC…………2
समीकरण 1 और 2 से
PQ∣∣SR और PQ=SR……….3
⇒□PQRS एक समांतर चतुर्भुज है।
अब ABCD एक आयत है।
∴AD=BF⇒12AD=12BC
⇒AS=BQ………4
ΔAPS और ΔBPQ से
AP=BP (P,AB का मध्य बिंदु है)
∠PAS=∠PBQ (प्रत्येक 90∘)
AS=BQ [समीकरण 4 से]
∴De<APS≅ΔBPQ (S.A.S प्रमेय )
⇒PS=PQ …….5
समीकरण 3 और 5 से
PQRS एक समांतर चतुर्भुज है तथा PS=PQ
∴PQRS एक समचतुर्भुज है।

Topper's Solved these Questions
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:प्रश्नावली 8.1
Explore 12 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:दीर्घ उत्तरीय प्रश्न
Explore 5 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
Explore 8 Videos
Similar Questions
एक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionएक चतुर्भुज के कोण 3:5:9:13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
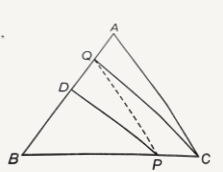
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
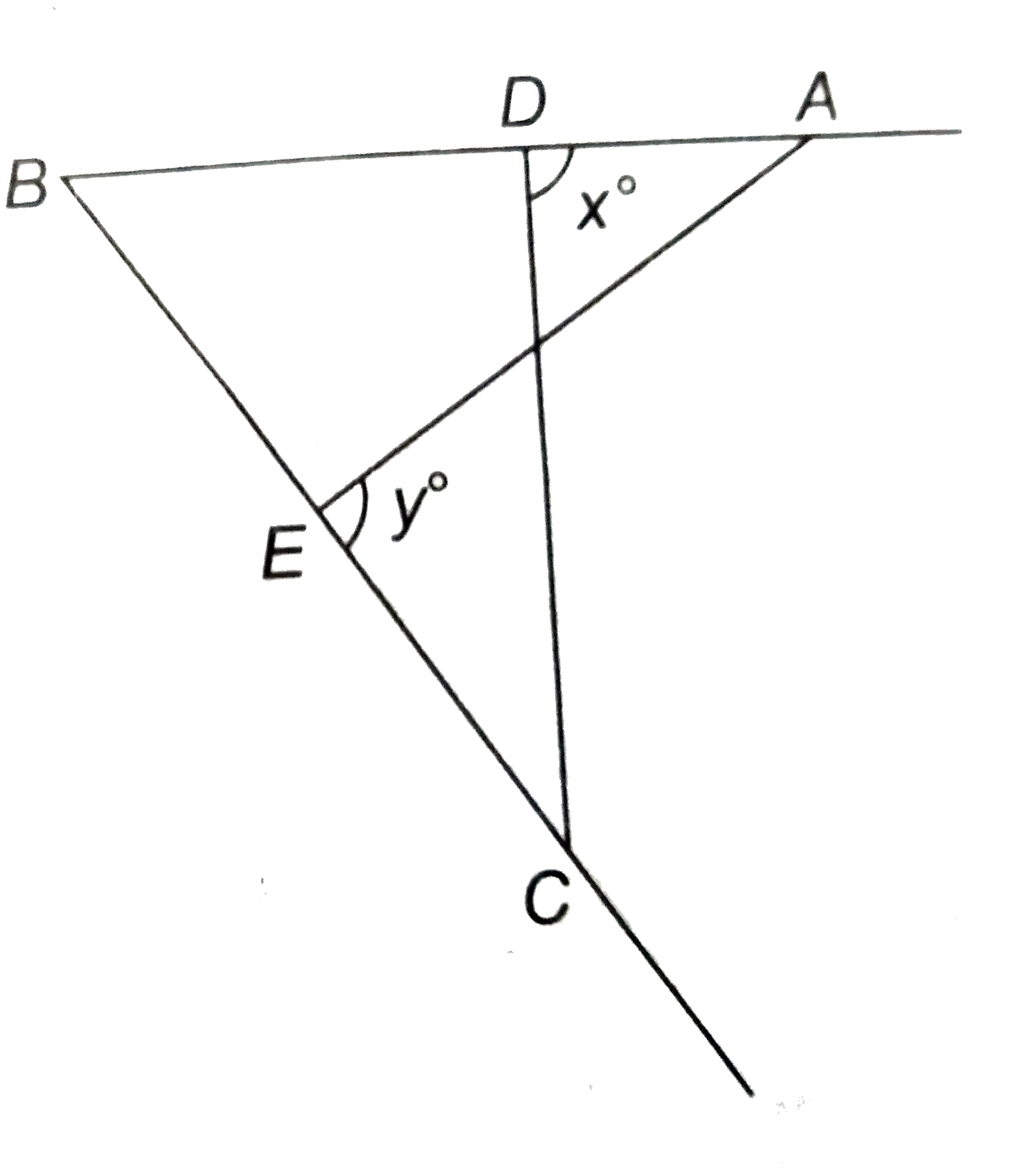
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View SolutionABCD एक समचतुर्भुज है। AB,BC,CD,DA के मध्य-बिंदु क्रमशः P,Q,R,S हैं। सिद्ध कीजिए कि PQRS एक आयत है।
View SolutionIn the given, ABCDEF is a regular hexagon of side 12cm. P, Q and R are the mid points of the sides AB, CD and EF respectively. What is the area (in cm^2 ) of triangle PQR? दी गई आकृति में , ABCDEF एक सम षट्भुज है जिसकी भुजा 12 से.मी.? है। P, Q तथा R क्रमशः भुजाओं AB, CD तथा EF के मध्य बिन्दु है। त्रिभुज PQR का क्षेत्रफल ( से.मी.^2 में) क्या है?
View SolutionABCD is a trapezium with AD and BC parallel sides. E is a point on BC. The ratio of the area trapezium ABCD to that of triangle AED is- ABCD एक AD और BC समांतर भुजाओं वाला समलंब चतुर्भुज है। E,BC पर एक बिंदु है। square ABCD और triangle AED के क्षेत्रफल का अनुपात क्या होगा?
View SolutionIn triangle ABC , P and Q are the middle points of the sides AB and AC respectively. R is a point on the segment PQ such that PR: RQ =1: 2. If PR = 2cm, then BC =? triangle ABC में, P और Q क्रमशः भुजाओं AB तथा AC के मध्य बिंदु हैं। R, PQ पर एक बिंदु इस प्रकार है कि PR: RQ =1: 2 यदि PR=2 सेमी, तो BC=
View SolutionA triangle PQR is a right angled triangle at Q. E and F are the mid points of QR and PR respectively. What will be the ratio of the area of quadrilateral PQEF to the area of triangle PQR. एक समकोण त्रिभुज PQR, E पर समकोण है E और F क्रमशः QR और PR के मध्य बिंदु हैं। चतुर्भुज PQEF के क्षेत्रफल और त्रिभुज PQR के क्षेत्रफल का अनुपात क्या होगा
View SolutionABCD is a quadrilateral such that angle D= 90^@ . A circle with centre O touches the sides AB, BC and CD and DA at P, Q, R and S respectively. If BC = 40 cm, BP = 28 cm and CD = 25 cm, then what is the radius of the circle is: ABCD एक चतुर्भुज है जैसे angle D= 90^@ । केन्द्र O वाला एक वृत्त क्रमशः AB, BC और CD और DA को P, Q,R और S से छूता है। यदि BC = 40 सेमी, BP = 28 सेमी और CD = 25 सेमी है, तो वृत्त का त्रिज्या क्या है
View SolutionIn a triangle ABC , the sides AB and AC are extended to P and Q respectively. The bisectors of angle PBC and angle QCB intersect at a point R. If angle R= 66^@ , then the measure of angle A is : त्रिभुज ABC में, AB और AC भुजाओं को क्रमशः P और Q तक बढ़ाया जाता है| angle PBC तथा angle QCB के द्विभाजक एक बिंदु R पर मिलते हैं | यदि angle R= 66^@ , है, तो कोण A का मान ज्ञात करें |
View SolutionA circle is inscribed in quadrilateral touching sides AB , BC , CD and AD at the points P , Q , R and S respectively. If BP = 4cm, SD = 6cm and BC = 7cm, then the length of DC is: एक वृत्त किसी चतुर्भुज के भीतर स्थित है जो भुजाओं AB, BC, CD और AD को क्रमशः P, Q, R और S पर स्पर्श करता है | यदि BP = 4 सेमी, SD = 6 सेमी और BC = 7 सेमी है, तो DC की लंबाई ज्ञात करें |
View Solution

