एक समांतर चतुर्भुज ABCD की भुजा AB का मध्य बिंदु P है। बिंदु B से होकर PD के समांतर रेखा DC को Q पर तथा बढ़ाई गई रेखा AD को R पर काटती है। सिद्ध कीजिए कि-
(i) AR=2BC (ii) BR=2BQ
ΔARB में
AB का मध्य बिंदु P है
और PD,BR के समांतर है।
∴D, भुजा AR का मध्य बिंदु होगा।
अर्थात AR=2AD
परंतु ABCD एक समांतर चतुर्भुज है।
∴AD=BC
अतः AR=2BC जो भाग (i) है।
□ABCD समांतर चतुर्भुज है।
⇒DC∣∣AB
⇒DQ∣∣AB
ΔRAB में
D,RA का मध्य बिंदु है।
तथा ∴Q,RB का मध्य बिंदु हेागा
⇒BR=2BQ
जो भाग (ii) है।

Topper's Solved these Questions
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:प्रश्नावली 8A
Explore 27 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:प्रश्नावली 8B
Explore 15 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:दीर्घ उत्तरीय प्रश्न
Explore 5 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
Explore 8 Videos
Similar Questions
एक चतुर्भुज के दो कोणों 89∘ और 113∘ है। यदि अन्य दो कोण बराबर है तो बराबर कोणों को ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।
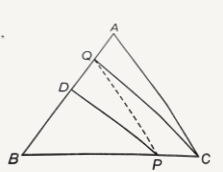
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
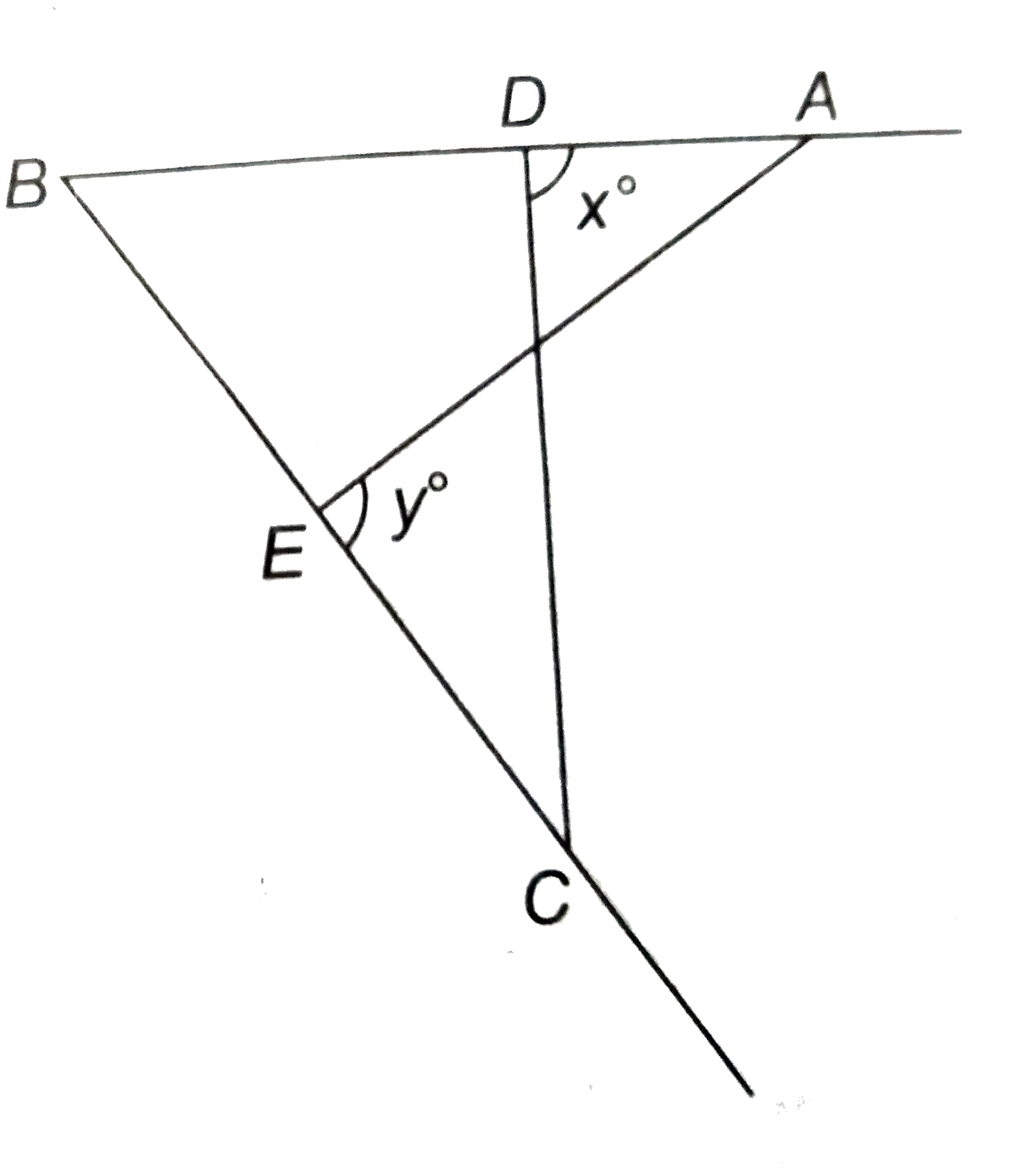
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionबिंदु A(1,2) से होकर जाने वाली रेखा X-अक्ष के साथ 60∘ का कोण बनाती है तथा x+y=6 को बिंदु P पर काटती है तो AP की लम्बाई ज्ञात कीजिए
View Solutionरेखा 3x+2y=6 अक्षो को बिन्दुओ A और B पर काटती है ।बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल10 वर्ग इकाई रहता है , तो P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionनिर्देशाक्षो को प्रारंभिक निर्देशांकों के समांतर रखते हुए मूल बिंदु को बिंदु P पर हटाने पर समीकरण ax+by+c=0 समीकरण ax+by+c+λ=0 के रूप में बदल जाता है सिद्ध कीजिए कि P बिन्दुपथ ax+by=λ होगा ।
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionसरल रेखा x+22=2y−76=5−z6 की दिक्- कोज्याएं ज्ञात कीजिए । साथ ही बिंदु A(−1,2,3) से होकर जाने वाली तथा दी हुई रेखा के समांतर रेखा का सदिश समीकरण ज्ञात कीजिए।
View Solutionसरल रेखा x−12=y−21=z+3−3 के समांतर उस रेखा के समीकरण ज्ञात कीजिए जो मूल बिंदु से होकर जाती है।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionएक रेखा बिंदु 2ˆi+ˆj−3ˆk से गुजरती है और साधीश ˆi+2ˆj+ˆk के समांतर है । रेखा का सदिश समाकरण ज्ञात कीजिए। इसके द्वारा रेखा का कार्तीय समीकरण ज्ञात कीजिए।
View Solutionमाना बिंदु (h,k), (1,2) तथा (−3,4) एक रेखा L1 पर स्थित है। यदि बिन्दुओ (h,k) तथा (4,3) से होकर जाने वाली रेखा L2 रेखा L1 के लंबवत है, तो kh बराबर है
View Solution