ABC एक त्रिभुज है जिसमे AC और AB पर खींचे गए शीर्षलाम्ब BE और CF बराबर है (देखिए आकृति)। दर्शाइए कि
(i) ΔABE≅ΔACF
(ii) AB=AC, अर्थात ΔABC एक समद्विबाहु त्रिभुज है।

(i) ΔABE≅ΔACF में,
∠AEB=∠AFC (प्रत्येक 90∘)
∠BAE=∠CAF (उभयनिष्ठ)
BE=CF (दिया है )
∴ΔABC≅ΔACF (A.A.S. से )
(ii) ∵ BE और CF शीर्षलाम्ब है।
∴∠1=∠2 (प्रत्येक 90∘)
अब ΔBFC और ΔBEC में,
∵⎧⎪
⎪⎨⎪
⎪⎩∠1=∠2 (दिया है)BC=BC (उभयनिष्ठ)CF=B {भाग (1) से}
∴ΔBFC≅ΔBEC (R.H.S.)
∴∠B=∠C (c.p.c.t.)
⇒AC=AB (समान कोणों कि सम्मुख भुजाएँ बराबर होती है )
ΔABC एक समद्विबाहु त्रिभुज है।

Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.3
5 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.4
6 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.1
8 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - विविध प्रश्नावली
12 Videos
Similar Questions
ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार है कि A और D भुजा BC के एक ही ओर स्थित है (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP, कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।

View Solutionदर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लम्बी भुजा होती है।
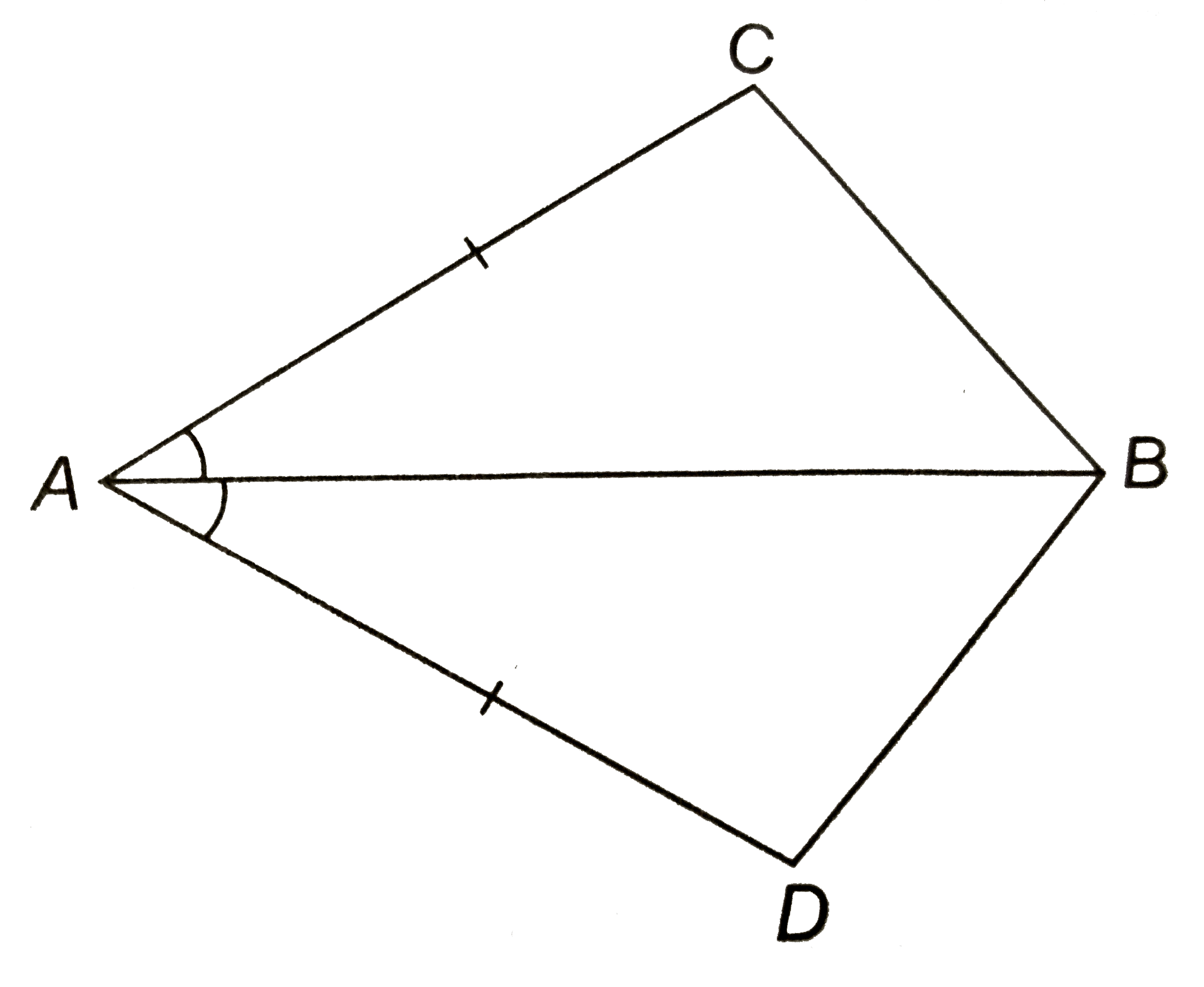
View Solutionचतुर्भुज ABCD में, AC =AD है और AB कोण A को समद्विभाजित करता है (देखिये आकृति )। दर्शाइए कि ΔABC≅ΔABD है।
BC और BD के बारे में आप क्या कह सकते है ?
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View SolutionIn triangle ABC, DE||BC where D is a point on AB and E is a point on AC. DE divides the area of triangle ABC into two equal parts.Then DB : AB is equal to एक त्रिभुज ABC DE||BC है जिसमें D,AB पर एक बिंदू है और E, AC पर एक बिंदू है। DE, triangle ABC के क्षेत्रफल को दो समान भागों में विभाजित करता है, DB : AB किसके बराबर हे?
View Solution
