समद्विबाहु त्रिभुज ABC के आधार BC पर कोई बिन्दु D है। सिद्ध कीजिए कि AB>AD और AC>AD.
Da<aABC में,
AB=AC
⇒∠ACB=∠ABC ......(1)
ΔABD में,
∠ADC=∠ABD+∠BAD
(∠ADC बहिष्कोण है)
⇒∠ADC>∠ABD
impliesangleADCgtangleACD" "[समीकरण(1)से]<br>impliesACgtAD<br>पुनःDeltaACDमें,<br>angleADB=angleACD+angleCAD" "(angleADBबहिष्कोणहै)<br>impliesangleADBgtangleACD<br>impliesangleADBgtangleABD" "[समीकरण(1)से]<br>impliesABgtAD

Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7A
30 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7B
19 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - विविध प्रश्नावली
12 Videos
Similar Questions
निम्नलिखित में से कौन-से त्रिभुजों के युग्म सर्वांगसम है ? प्रत्येक में सर्वागसमता का प्रतिबन्ध भी बताइए :
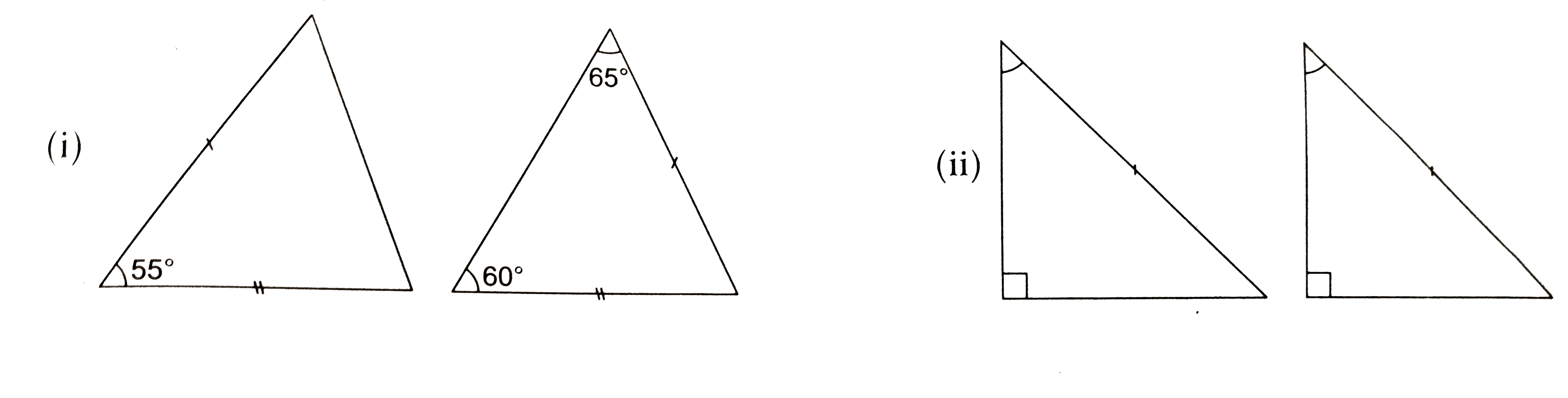
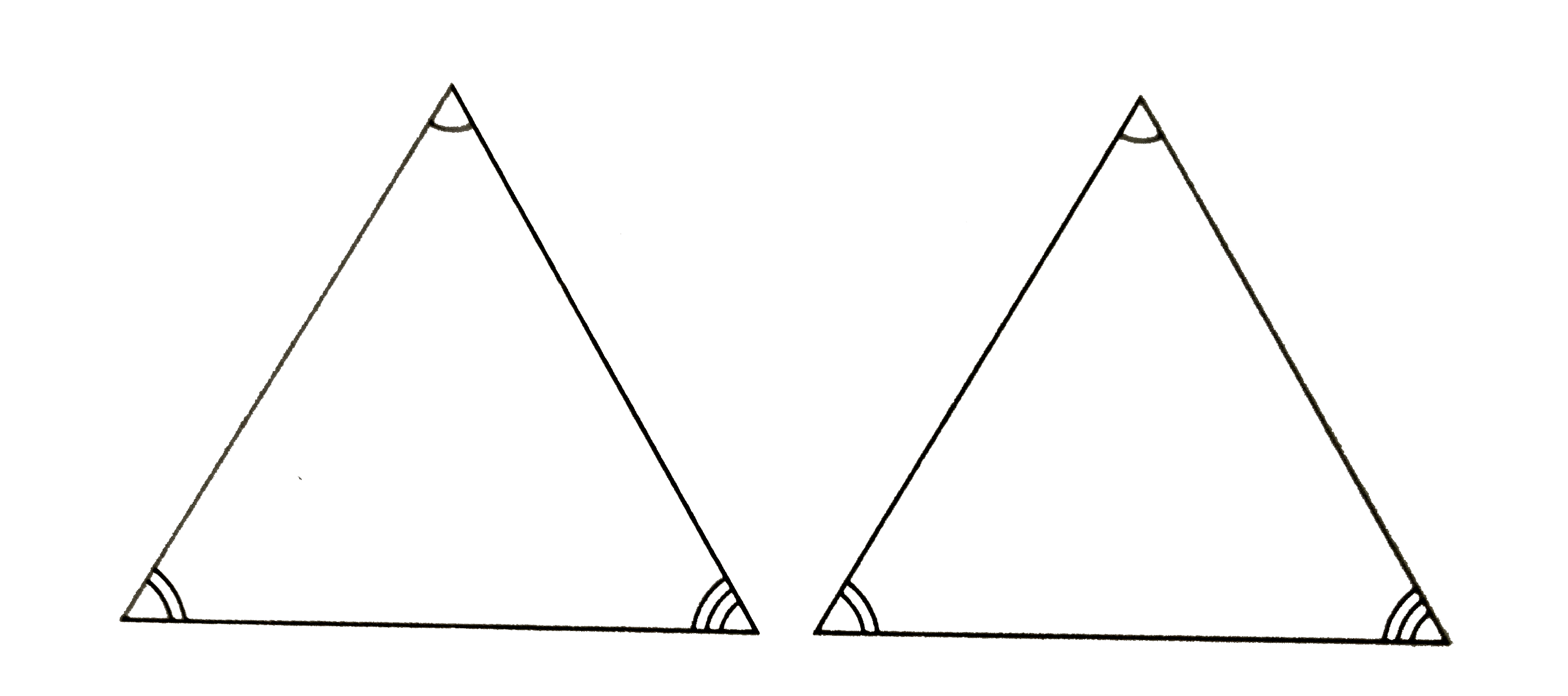
View SolutionΔABC में, AB=8 सेमी, BC = 15 सेमी और AC = 17 सेमी है। सबसे कोण ज्ञात कीजिए।
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
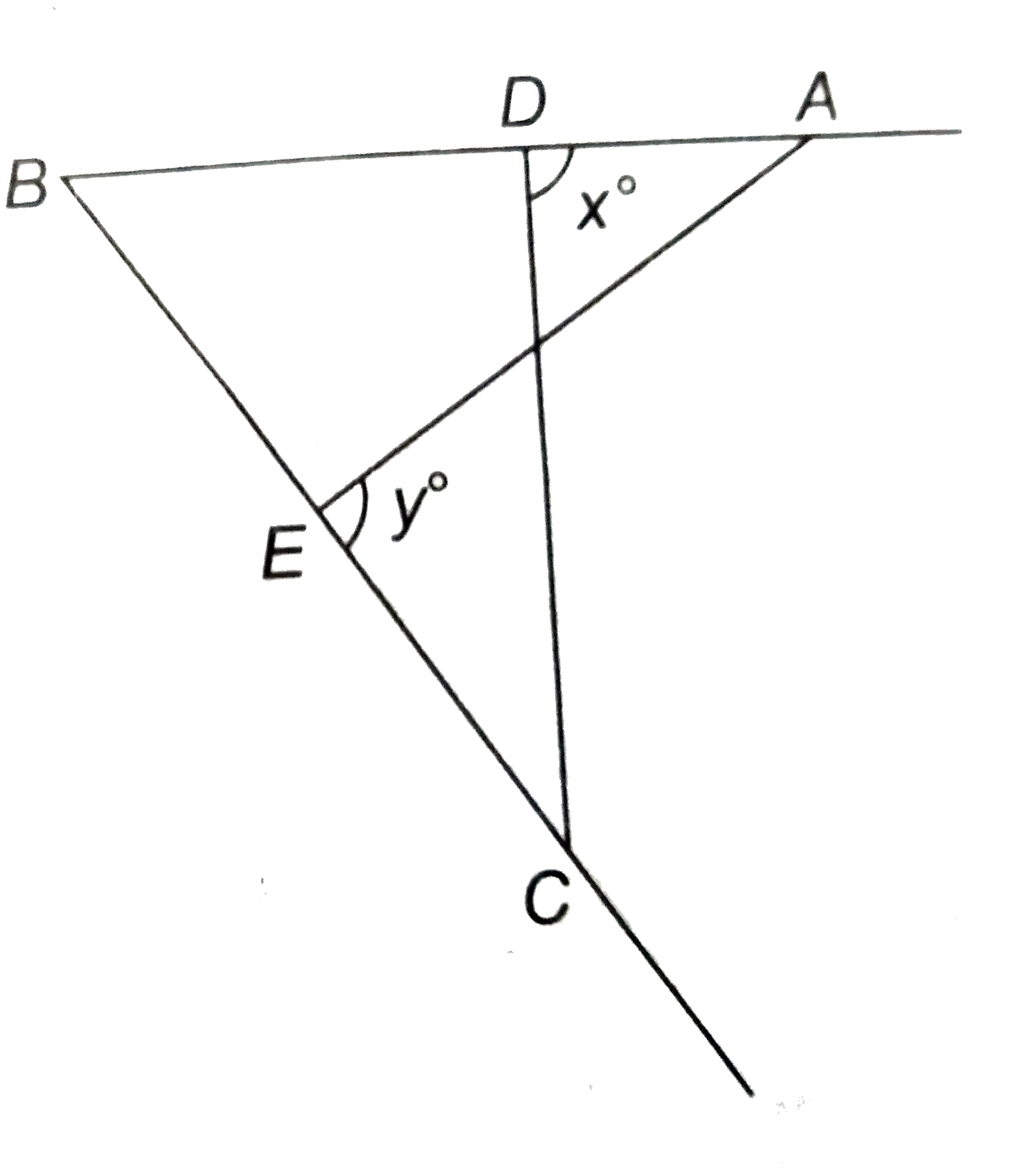
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=0
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionत्रिभुज के आधार पर कुछ महत्वपूर्ण प्रश्न
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionयदि A, B, C, D समष्टि (space) में चार बिन्दु हैं, तो सिद्ध कीजिए कि |AB×CD+BC×AD+CA×BD|=4 ( त्रिभुज ABC का क्षेत्रफल )
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,5), (6,3) और (5,10)
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(1,1), (-1,-1) और (−√3,√3)
View Solution
