एक त्रिभुज ABC में, ∠B=2∠C है। BC पर एक बिन्दु D इस प्रकार है कि AD, ∠BAC को समद्विभाजित करता है और AB =CD है। सिद्ध कीजिए कि ∠BAC=72∘
माना ∠ABC का समद्विभाजक BP है। PD को मिलाया।
माना ∠BAD=∠DAC=x
माना ∠ABP=∠PBC=y
अब, ∠B=2∠C
⇒2y=2∠C
⇒∠C=y
∵∠PBD=∠PCD=y
⇒PB=PC ......(1)
अब ΔABP और ΔDCP में,
∵⎧⎪
⎪⎨⎪
⎪⎩AB=DC (दिया है )∠ABP=∠DCP (प्रत्येक y के बराबर है )PB=PC (दिया है )
∴ΔABP≅ΔDCP (S.A.S.)
∴∠BAP=∠CDP (c.p.c.t.)
⇒∠CDP=2x और AP=DP (c.p.c.t.)
∴∠PDA=∠PAD=x
ΔABD में, ∠ADC बहिष्कोण है।
∴∠CDP+∠ADP=x+2y (बाह्य कोण)
⇒2x+x=x+2y⇒x=y
अब ΔABC में,
∠A+∠B+∠C=180∘ (कोण-योग गुण )
⇒2x+2y+y=180∘
⇒2x+2x+x=180∘ (∵x=y)
⇒5x=180∘⇒x=36∘
⇒∠BAC=2x=72∘

Topper's Solved these Questions
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:साधित उदाहरण
Explore 11 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:प्रश्नावली 7A
Explore 30 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
- दो चरों वाले रैखिक समीकरण Book:NOOTAN HINDIChapter:दो चरों वाले रैखिक समीकरण Exercise:विविध प्रश्नावली
Explore 12 Videos
Similar Questions
ΔABC में, ∠A=100∘,∠C=30∘ है। ΔABC (i) सबसे बड़ी (ii) सबसे छोटी भुजा कौन-सी है?
View Solutionनिम्नलिखित में से कौन-से त्रिभुजों के युग्म सर्वांगसम है ? प्रत्येक में सर्वागसमता का प्रतिबन्ध भी बताइए :
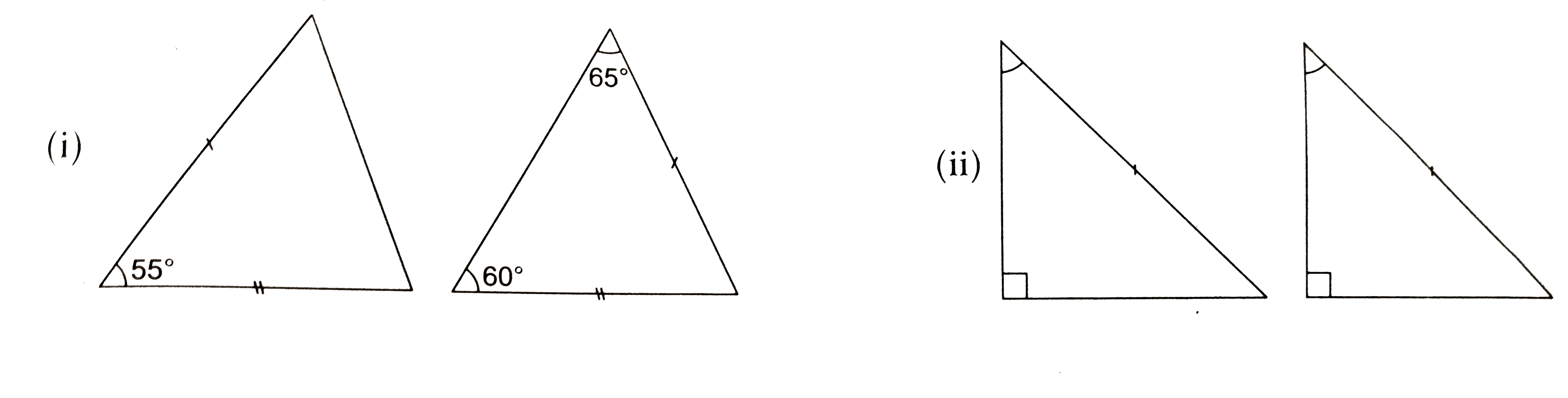
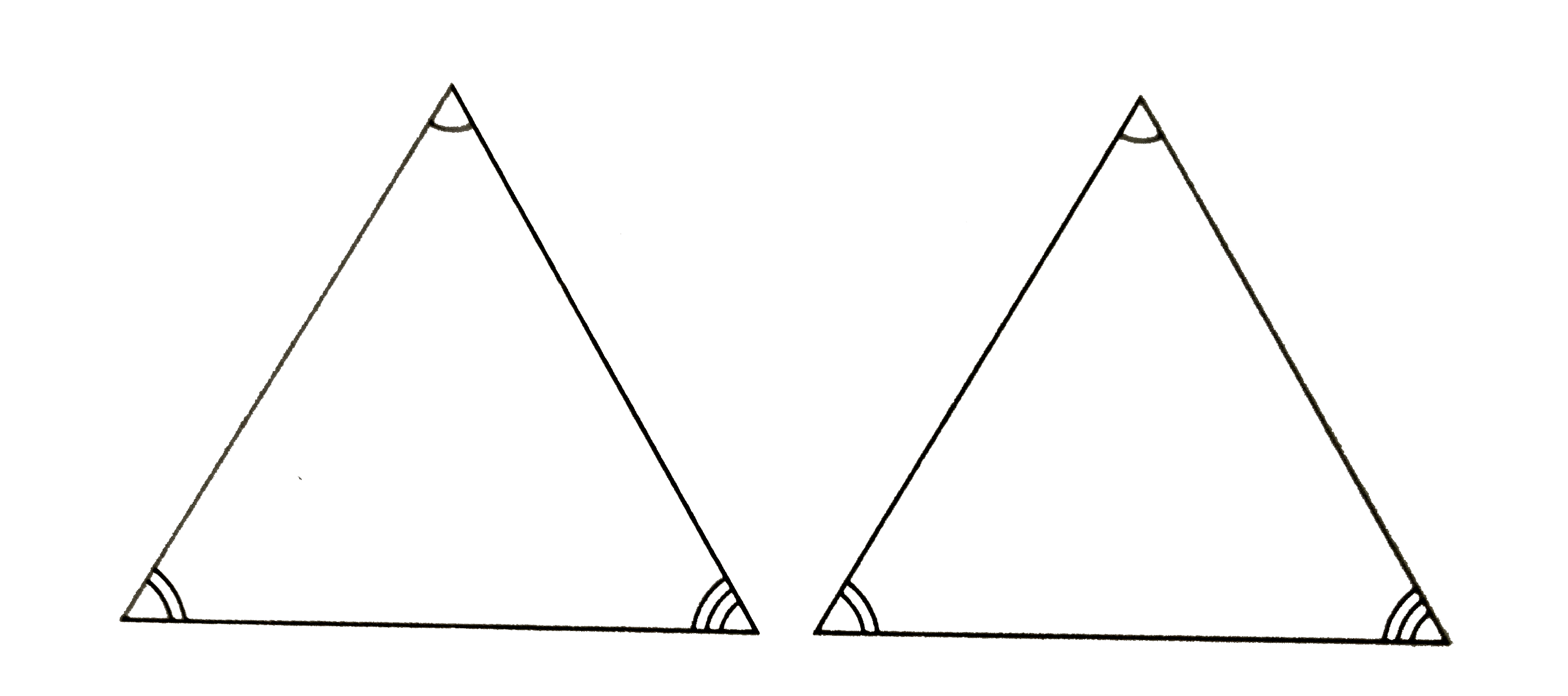
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionकिसी त्रिभुज ABC में A और B स्थिर बिंदु है । शीर्ष C इस प्रकार गमन करता है कि cotA+cotB=λ, जहाँ λ अचर है । C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solution

