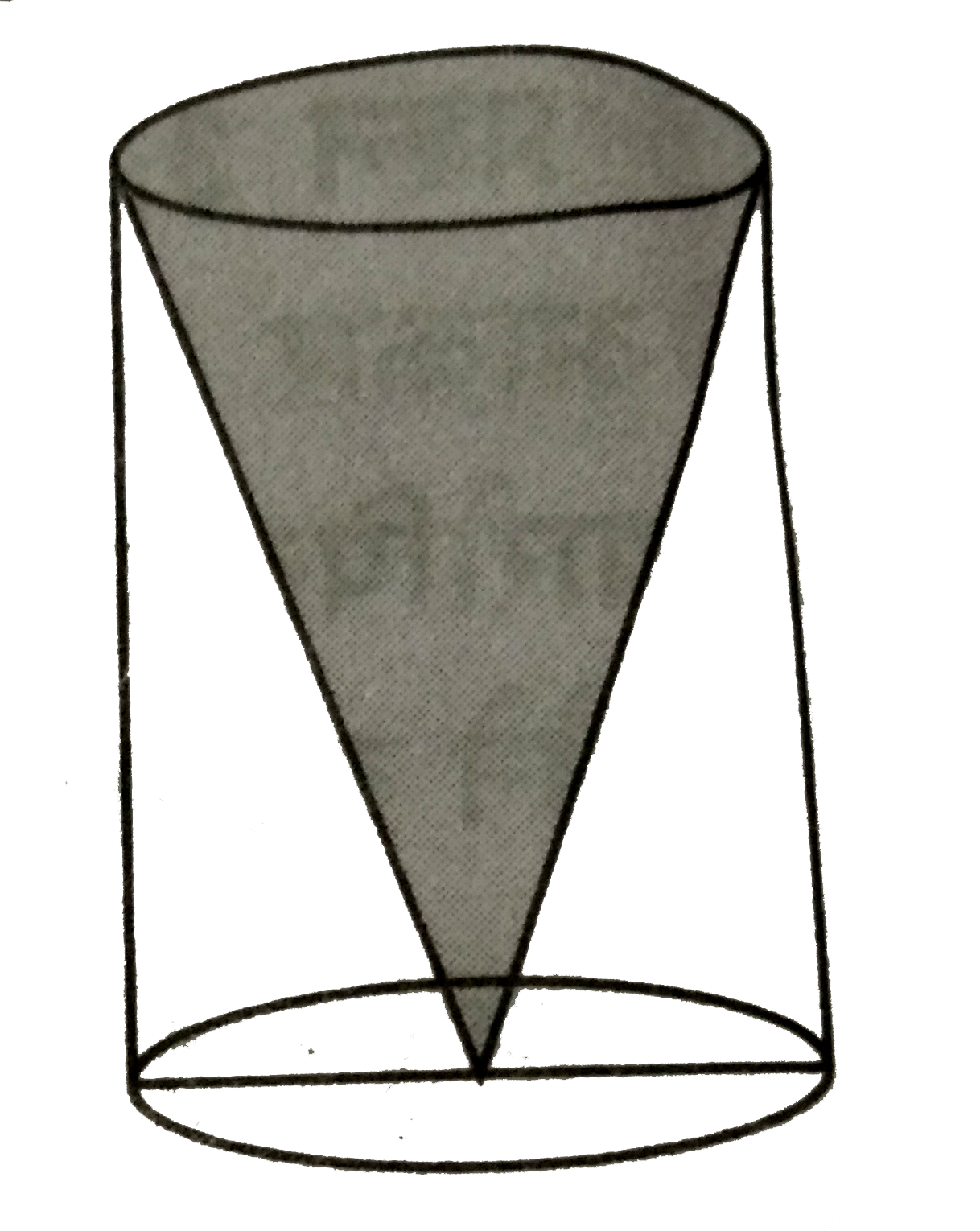
ऊँचाई 2⋅4 सेमी और व्यास 1⋅4 सेमी वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल काट लिया जाता है | शेष बचे ठोस का निकटतम वर्ग सेन्टीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
बेलन का व्यास 2r=1.4 सेमी
⇒r=0.7 सेमी
∴ बेलन की त्रिज्या = शंकु की त्रिज्या r=0.7 सेमी
बेलन की ऊंचाई = शंकु की ऊंचाई =h=2.4 सेमी
यदि शंकु की तिर्यक ऊंचाई l है , तो
l2=h2+r2=(2.4)2+(0.7)2=5.76+0.49=6.25
⇒l=√6.25=2.5 सेमी
शेष ठोस का पृष्ठीय क्षेत्रफल = बेलन के आधार का क्षेत्रफल + बेलन का वक्रपृष्ठ + शंकु का वक्रपृष्ठ
=πr2+2πrh+πrl
=πr(r+2h+l)
=227×0.7×(0.7+2×2.4+2.5)
=2.2×8=17.6सेमी2
Topper's Solved these Questions
- पृष्ठीय क्षेत्रफल और आयतन Book:NOOTAN HINDIChapter:पृष्ठीय क्षेत्रफल और आयतन Exercise:ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.2)
Explore 8 Videos
- पृष्ठीय क्षेत्रफल और आयतन Book:NOOTAN HINDIChapter:पृष्ठीय क्षेत्रफल और आयतन Exercise:ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.3)
Explore 9 Videos
- पृष्ठीय क्षेत्रफल और आयतन Book:NOOTAN HINDIChapter:पृष्ठीय क्षेत्रफल और आयतन Exercise:प्रश्नावली 13C
Explore 8 Videos
- निर्देशांक ज्यामितिBook:NOOTAN HINDIChapter:निर्देशांक ज्यामितिExercise:बहुविकल्पीय प्रश्न
Explore 7 Videos
- प्रायिकता Book:NOOTAN HINDIChapter:प्रायिकता Exercise:बहुविकल्पीय प्रश्न
Explore 7 Videos
Similar Questions
एक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिसकी त्रिज्याएँ 1 सेमी है तथा शंकु की ऊंचाई उसकी त्रिज्या के बराबर है । इस ठोस का आयतन π के पदों में ज्ञात कीजिए ।
View Solutionत्रिज्या 4.2 सेमी वाले धातु के एक गोले को पिघलाकर त्रिज्या 6 सेमी वाले एक बेलन के रूप में डाला जाता है बेलन की ऊंचाई ज्ञात कीजिए ।
View Solution24 सेमी ऊँची बाल्टी के सिरों की त्रिज्याएँ 15 सेमी और 5 सेमी है । इसकी धारिता ज्ञात कीजिए । बाल्टी का पृष्ठ भी ज्ञात कीजिए ।
View Solutionबिंदु (3, 4) की x-अक्ष से दूरी है :
View Solutionकिसी निश्चित घटना की प्रायिकता है :
View Solutionएक △ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AG=6 सेमी , BE=12.6 सेमी और FG=3 सेमी हो , तो AD ,GE और GC ज्ञात कीजिए।
View Solutionएक वृत्त का केंद्र (2x−1,3x+1) है। x ज्ञात कीजिए यदि वृत्त (-3,-1) में से गुजरे और व्यास की लम्बाई 20 मात्रक हो।
View Solution10 सेमी. व्यास वाले अर्धगोले का सम्पूर्ण पृष्ट को क्षेत्रफल ज्ञात कीजिए|
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View Solutionएक धातु के बेलन को, जिसका व्यास 8 से.मी. और ऊँचाई 90 से. मी. है, गलाकर 12 से. मी. व्यास वाले कितने गोले बनाए जा सकते हैं ?
View SolutionRevision#!#पृष्ठीय क्षेत्रफल और आयतन #!#एक ठोस का दूसरे ठोस में रूपांतरण
View SolutionA hollow cylinder of thickness 0.7 cm and height 15cm is made of iron. If inner radius of cylinder is 3.5 cm, then what is the total surface area (in cm^2 ) of the hollow cylinder? एक लोहे से बने बेलन की चौड़ाई 0.7 सेमी. तथा ऊँचाई 15 सेमी. है। यदि बेलन की आंतरिक त्रिज्या 3.5 सेमी. है, वो खाली बेलन का कुल पृष्ठीय क्षेत्रफल ( सेमी^2 में) क्या है?
View SolutionThe diameters of the internal and external surfaces of a hollow spherical shell are 6 cm and 10 cm respectively. If it is melted and made of solid cylinder of length 8/3 cm, then the diameter (in cm) of the cylinder is- एक खोखले गोलाकार खोल की आंतरिक एवं बाहरी सतहों का व्यास क्रमशः 6 सेमी ओर 10 सेमी है। यदि इसे गलाकर 8/3 सेमी लंबाई का ठोस बेलन बनाया जाता है, तो बेलन का व्यास (सेमी में) कितना होगा?
View SolutionFrom a solid right circular cylinder of length 4 cm and diameter 6 cm, conical cavity of the same height and base is hollowed out. The whole surface of the remaining solid (in, square cm) is 4 सेमी लंबाई और 6 सेमी व्यास के एक ठोस लम्ब वृत्तीय बेलन से, समान ऊंचाई ओर आधार के शंक्वाकार छिद्र कर निकाल लिया जाता है। तो शेष ठोस का (वर्ग सेमी में) सम्पूर्ण पृष्ठ क्षेत्रफल हैः
View SolutionAssume that a drop of water is spherical and its diameter is one-tenth of a cm. A conical glass has a height equal to the diameter of its rim. If 32000 drops of water can fill the glass completely, then the height of the glass (in cm.) is मान लें कि पानी को एक बूंद गोलाकार है और इसका व्यास एक सेमी का दसवां हिस्सा है। एक शंक्वाकार गिलास की ऊँचाई, उसके आधार (rim) के व्यास के बराबर है। यूदि 32000 पानी की बूंदें गिलास को पूरी तरह से भर देती हैं, तो गिलास को ऊँचाई (सेमी में) कितना है?
View Solution

