सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए |
(1+tanθ+secθ)(1+cotθ−cosecθ) बराबर है :
The correct Answer is:c
(1+tanθ+secθ)(1+cotthea−cosecθ)
=1+cotθ−cosecθ+tanθ+tanθ⋅cotθ
−tanθ⋅cosecθ+secθ+secθ⋅cotθ−secθ⋅cosecθ
=1+cotθ−cosecθ+tanθ
+sinθcosθ⋅cosθsinθ−sinθcosθ⋅1sinθ+secθ
+1cosθ⋅cosθsinθ−secθcosecθ
=1+(cotθ+tanθ)−cosecθ)
+1−secθ+secθ+cosecθ
−secθcosecθ
=2+(cosθsinθ+sinθcosθ)−secθcosecθ
=2+cos2θ+sin2θsinθ⋅cosθ−secθcosecθ
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति का परिचय EXERCISE - विविध प्रश्नावली38videos
त्रिकोणमिति का परिचय
- BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति का परिचय EXERCISE - लघु उत्तरीय प्रश्न34videos
त्रिकोणमिति का परिचय
- BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति का परिचय EXERCISE - प्रश्नावली 8.311videos
त्रिकोणमिति का परिचय
- BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)6videos
त्रिकोणमिति के कुछ अनुप्रयोग
Similar Questions
यदि tanθ=34, तो cosθ का मान ज्ञात कीजिए |
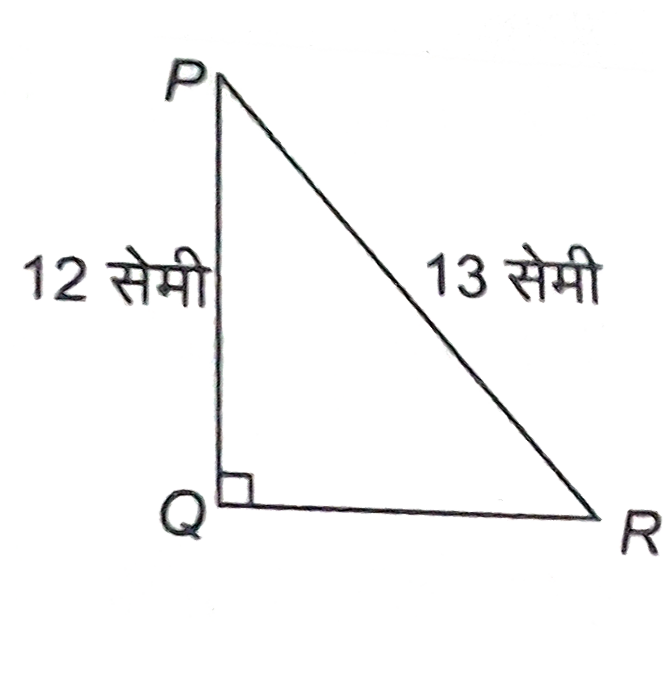
02:58View Solutionसंलग्न चित्र में tan P - cos R का मान ज्ञात कीजिए |
01:47View Solutionsin18∘cos72∘ मान निकालिए :
02:01View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
02:48View Solution(sec theta+tan theta)/(csc theta+cot theta)=(csc theta-cot theta)/(sec theta-tan theta)
04:16View Solution(tan theta)/(sec theta+1)+(cot theta)/(csc theta+1)=csc theta+sec theta-csc theta sec theta
06:43View Solutiontanθ1−cotθ+cotθ1−tanθ=1+secθcosecθ
04:18View Solutionprove that tan theta/(sec theta+1)+cot theta/(cosec theta+1)=cosec theta+sec theta-cosec theta. sec theta
03:18View Solution(1+cotθ−cosecθ)(1+tanθ+secθ)=
06:34View Solutionसिद्ध कीजिए : tanθ1−cotθ+cotθ1−tanθ=1+secθ cosec θ
03:56View Solutiontanθ1−cotθ+cotθ1−tanθ=1+secθcosecθ
07:09View Solution(1+tanθ+secθ)(1+cotθ−cosecθ)=
04:58View Solutionsecθ+tanθcosec θ+cotθ−secθ−tanθ cosecθ−cotθ=
05:34View Solution(1+cotθ−cosecθ)(1+tanθ+secθ)=?
04:29View SolutionProve that :
tanθ1−cotθ+cotθ1−tanθ=1+secθcosecθ .06:01View SolutionExpression (tan theta ) / (1-cot theta ) + (cot theta)/(1 - tan theta)- sec theta " cosec" theta The value of
02:51View Solution