चित्र में DE||BC और AD:DB = 5:4 है तो ar(ΔDEF)ar(ΔCFB) ज्ञात कीजिये
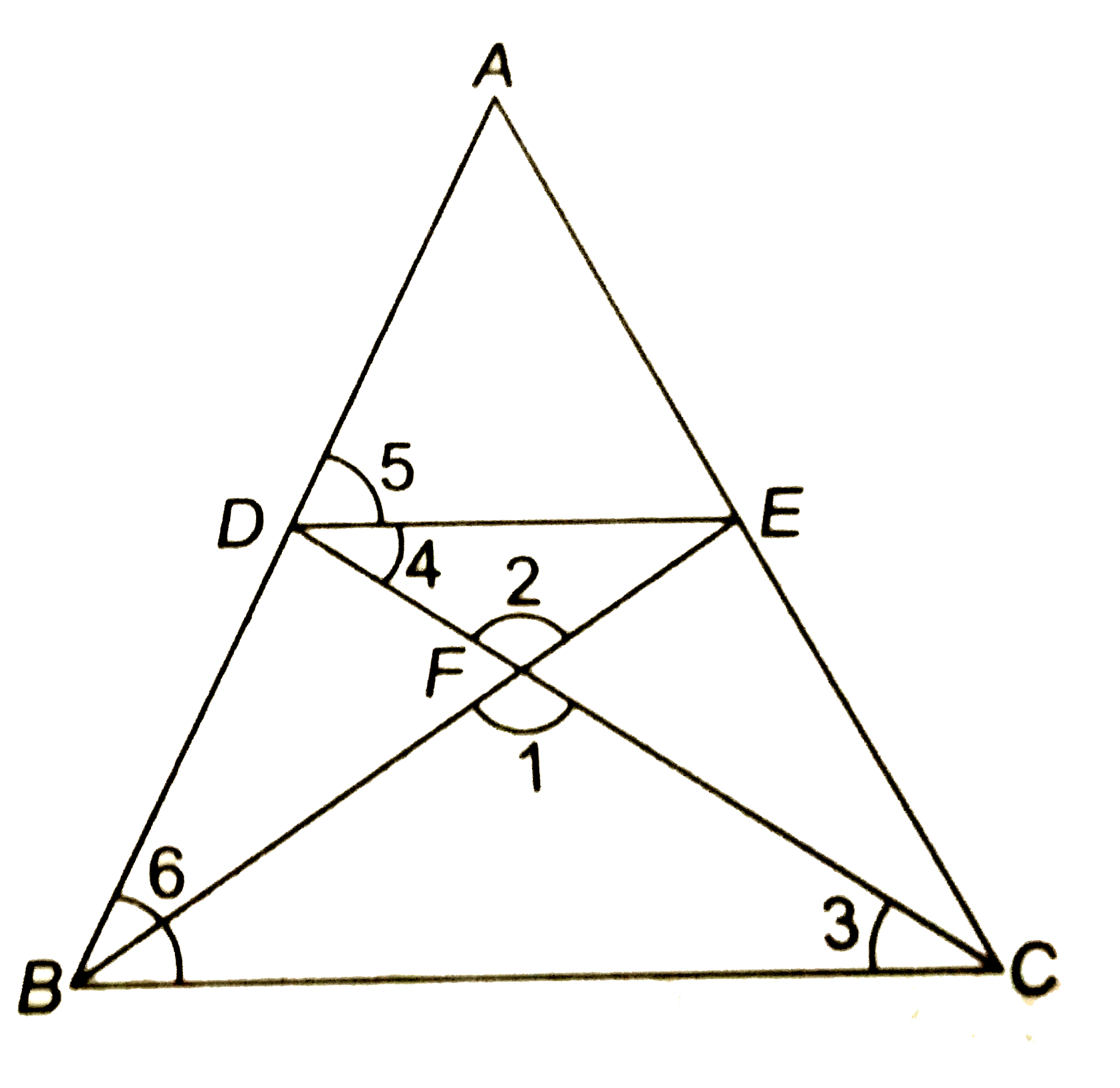
∴DE||BC
∴ ΔADE और ΔABC में
∴ ∠5=∠6 (संगत कोण)
और ∠A=∠A (उभयनिष्ठ)
∴ ΔADE~ΔABC (AA उपप्रमेय)
∴ ADAB=DEBC
⇒ ADAD+DB=DEBC ⇒ BCDE=AD+BDAD
⇒ BCDE=1+BDAD⇒BCDE=1+45 (∴ADBD=54, दिया है)
⇒ BCDE=95
∴ DEBC=59
ΔDEF और ΔCFB में
∠4=∠3 (एकान्तर कोण , ∴DE||BC)
और ∠2=∠1 (शीर्षभिमुख कोण)
∴ ΔDEF~ΔCBF (AA उपप्रमेय)
∴ ar(ΔDEF)ar(ΔCBF)=DE2BC2=(59)2
अतः ar(ΔDEF)ar(ΔCBF)=2581
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6A24videos
त्रिभुज
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6B26videos
त्रिभुज
- BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)6videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - NOOTAN HINDICHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)7videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
संलग्न चित्र में , बिन्दु D , AB को 3:5 में विभाजित करता है ज्ञात कीजिये
(i) AEEC (ii) ADAB (iii) AEAC
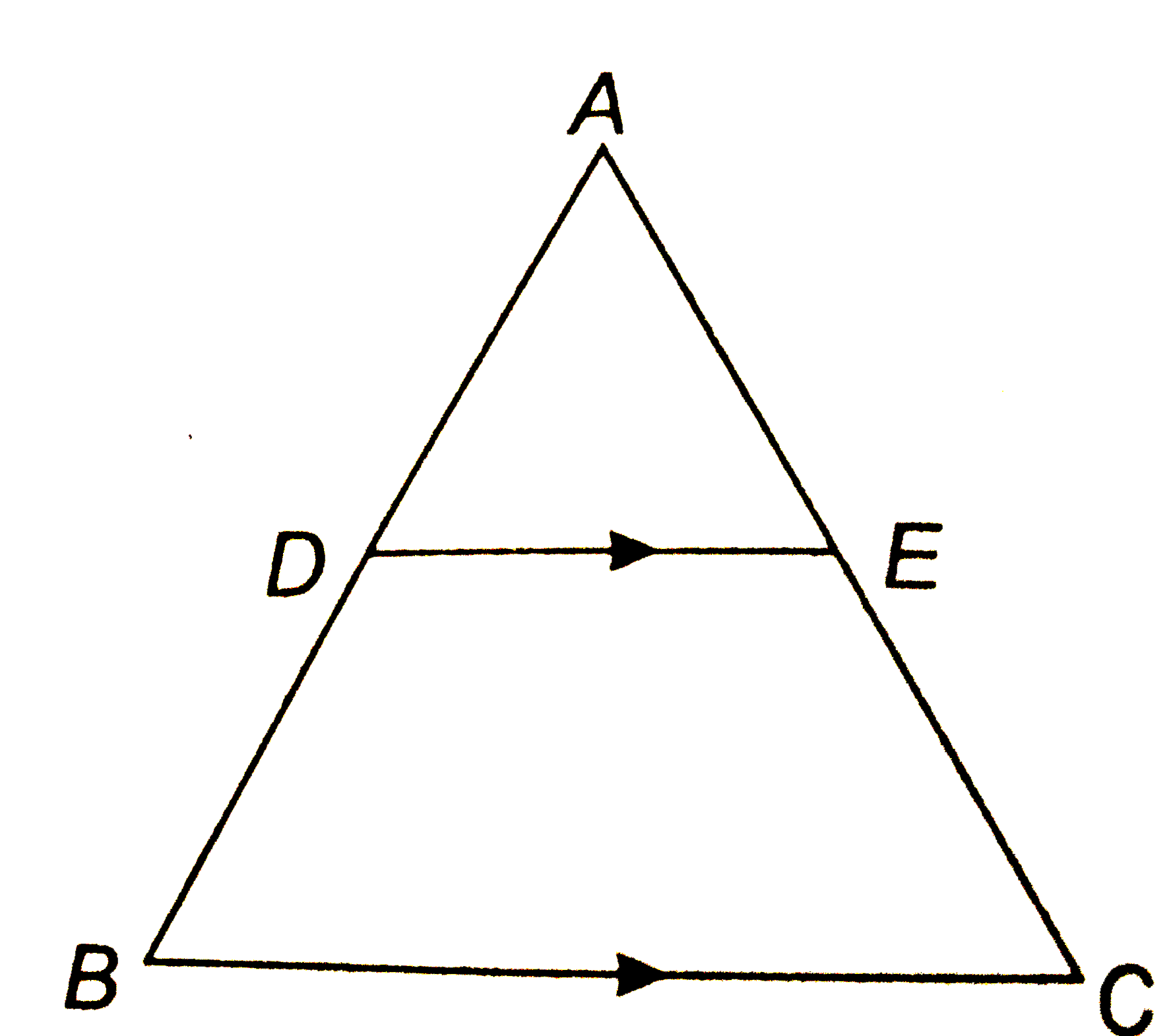 01:37View Solution
01:37View Solutionदिए चित्र में यदि, AB||CD तो सिद्ध कीजिये कि ΔAOB~ΔDOC
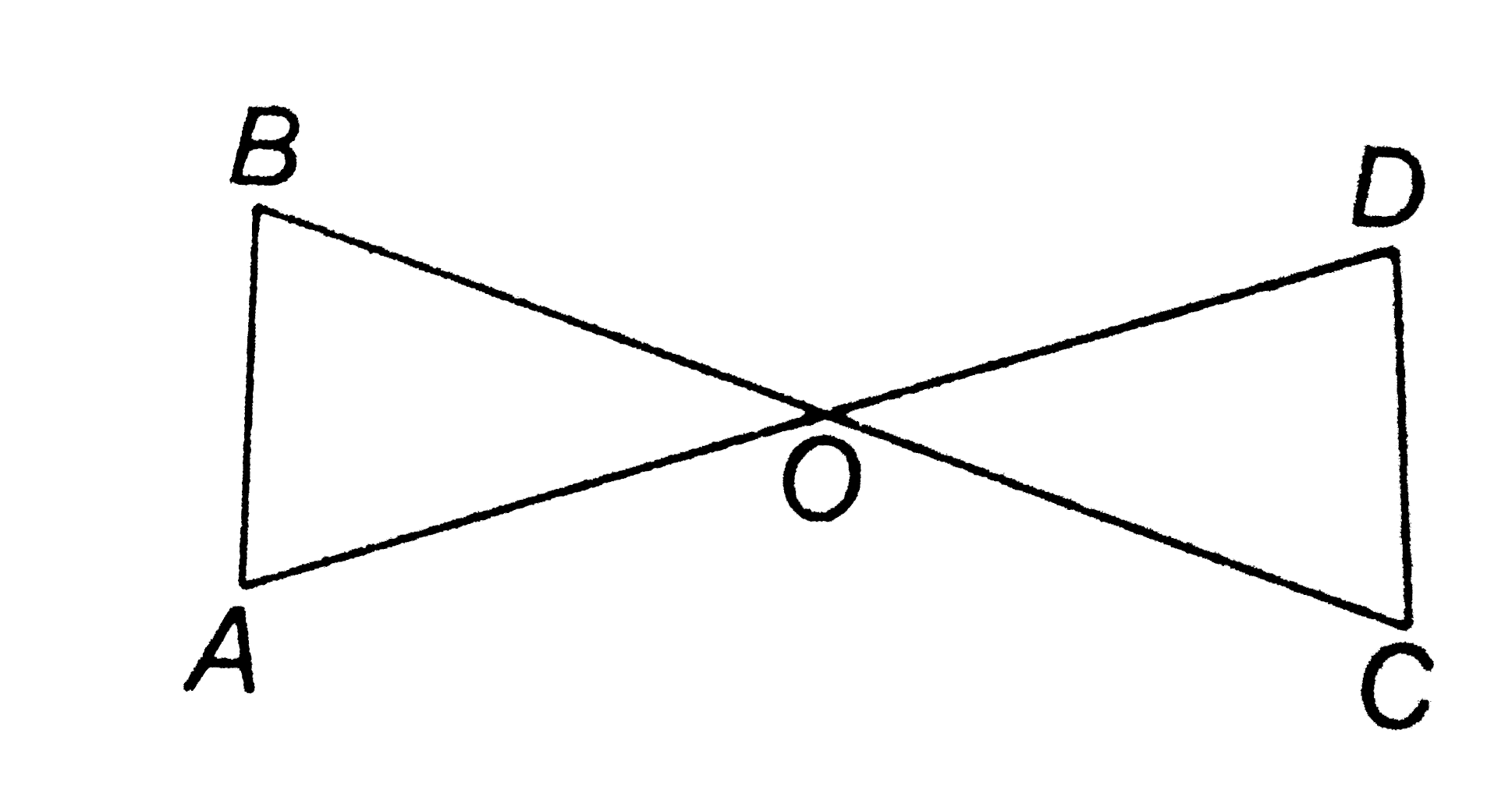 06:07View Solution
06:07View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
02:11View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
01:31View SolutionHow many lines of symmetry does the above figure have ?
02:45View SolutionWhich of the following are correct chain isomers of butane ? (i)
02:17View SolutionDetermine the point of symmetry of a regular hexagon.
05:41View SolutionDtermine the images of the following figure about the given line :
02:21View SolutionMatch the following Column A to Column B
 02:03View Solution
02:03View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionFind the area of the figure given below.
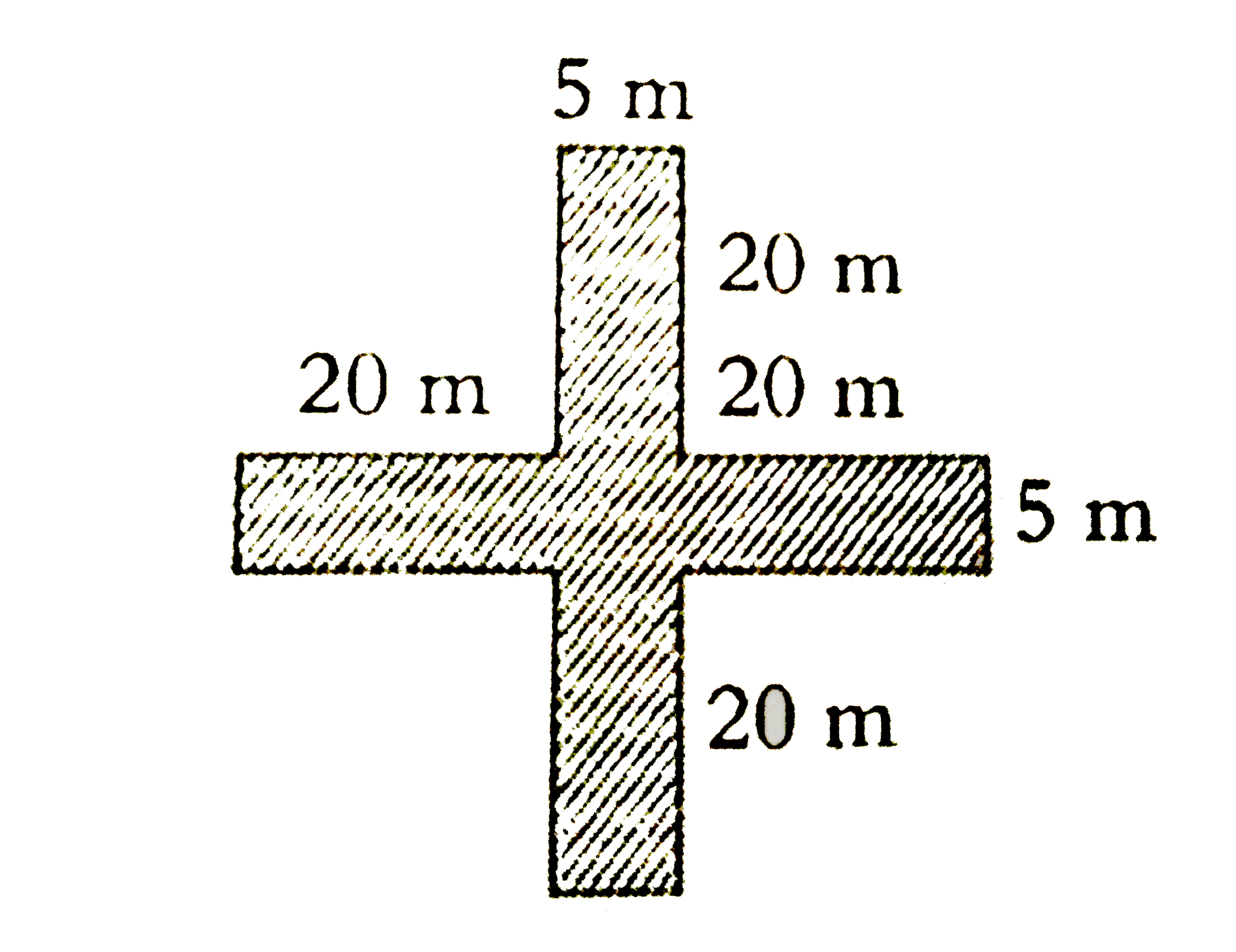 02:10View Solution
02:10View SolutionThe area of the shaded part in the figure given below is ______.
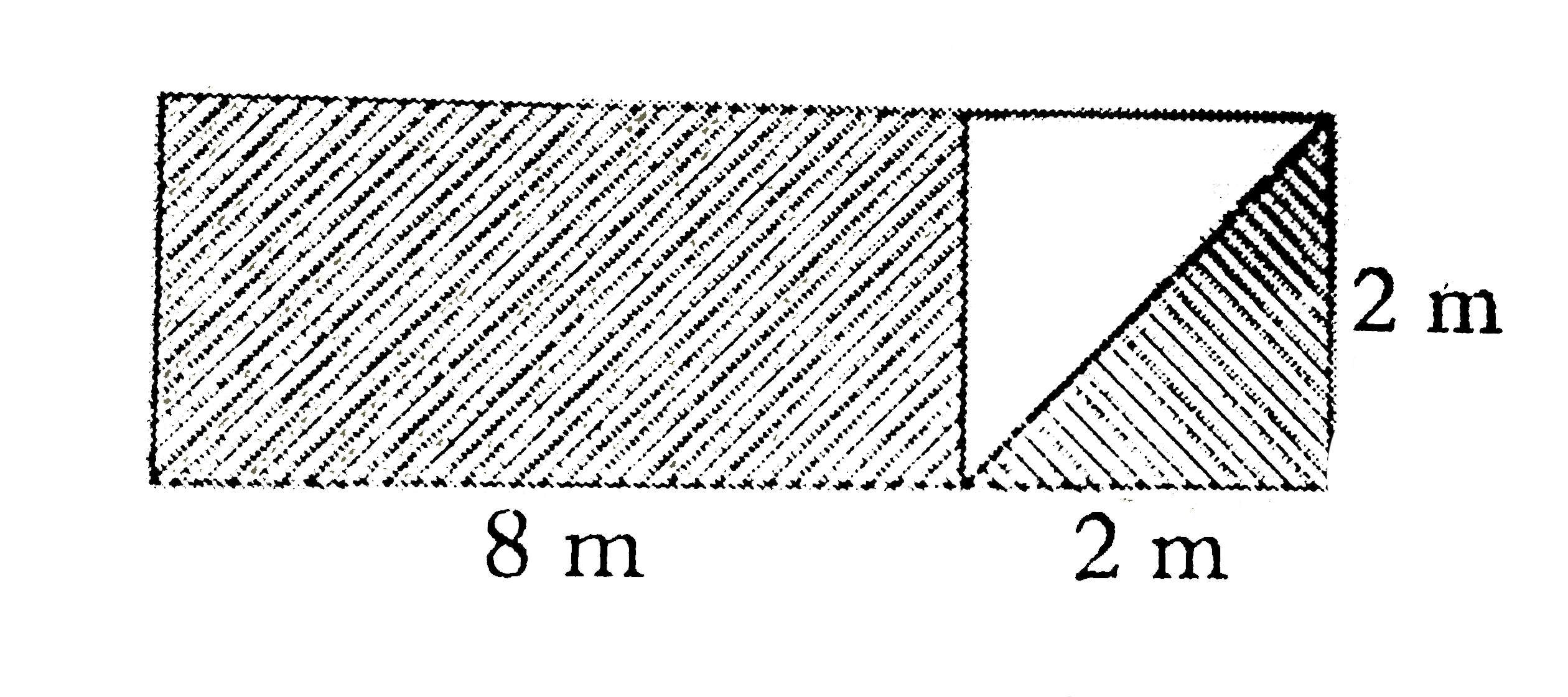 04:23View Solution
04:23View SolutionThe inequation represented by the graph given below is :
03:12View SolutionThe inequation that best describes the graph given below is _________
09:18View SolutionThe inequation that best describes the following graph is _________
03:10View Solution

