यदि किसी A.P. के प्रथम 7 पदों का योग 49 है और प्रथम 17 पदों का योग 289 है, तो इसके प्रथम n पदों का योग ज्ञात कीजिए|
माना A.P. का प्रथम पद a तथा सार्वान्तर d है|
अब, S7=49
⇒ 72[2a+(7−1)]=49⇒ 12[2a+6d]=7
⇒ a+3d=7 ...(1)
तथा S17=289
⇒172[2a+(17−1)d]=289
⇒ 12[2a+16d]=17⇒a+8d=17....(2)
समीकरण (2 ) से (1 ) को घटाने पर
a+8d=17
a+3d=7
⇒ d=2
d का मान समीकरण (1 ) में रखने पर
a+3×2=7 ltbr gt ⇒ a+=7
⇒ a=7−6=1
अब, Sn=n2[2a+(n−1)d]
=n2[2×1+(n−1).2]
=n(1+n−1)=n2
∴A.P. के n पदों का योग =n2
Topper's Solved these Questions
- समान्तर श्रेढ़ी BOOK - NOOTAN HINDICHAPTER - समान्तर श्रेढ़ी EXERCISE - प्रश्नावली 5.4
5 Videos
- समान्तर श्रेढ़ी BOOK - NOOTAN HINDICHAPTER - समान्तर श्रेढ़ी EXERCISE - विविध प्रश्नावली (अतिलघु उतरिए प्रश्न)
10 Videos
- समान्तर श्रेढ़ी BOOK - NOOTAN HINDICHAPTER - समान्तर श्रेढ़ी EXERCISE - प्रश्नावली 5.2
21 Videos
- वृत्तों से समबन्धित क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - विविध प्रश्नावली ( बहुविकल्पीय प्रश्न )
14 Videos
- सांख्यिकीBOOK - NOOTAN HINDICHAPTER - सांख्यिकीEXERCISE - बहुविकल्पीय प्रश्न
7 Videos
Similar Questions
A.P.:121,117,113,.... कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
View Solutionk किस मान के लिए 2k−1,7 और 3k,A.P. में है?
View Solutionनिम्नलिखित सारणी में,रिक्त स्थानों को भरिए,जहाँ AP का प्रथम पद a सार्वान्तर d और n वां पद an है:
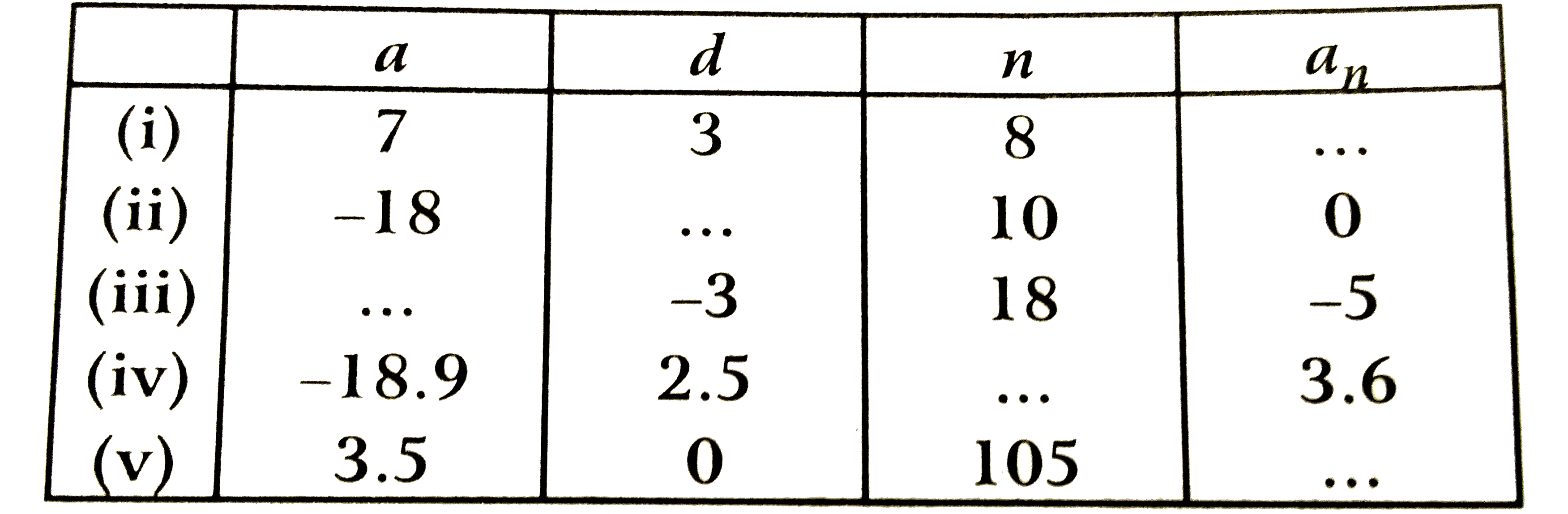
View Solutionयदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग R त्रिज्या के वृत्त की परिधि के बराबर है , तो :
View Solutionवर्गीकृत आंकड़ों का माध्य ज्ञात करने के लिए सूत्र ¯x=a+ΣfiΣfi में di निम्नलिखित के a विचलन है
View Solutionएक समान्तर श्रेढ़ी में पदों की संख्या सम ( even ) है| उसके विषम पदों का योग 24 तथा सम पदों का योग 30 है और अंतिम पद, प्रथम पद से 1012 अधिक है | पसं की संख्या एवं श्रेढ़ी ज्ञात कीजिए |
View Solutionनिम्नलिखित श्रेणियों का n पदों तक योग ज्ञात कीजिए ।
1+32+54+78+…............
View Solutionनिम्नलिखित श्रेणियों का n पदों तक योग ज्ञात कीजिए :
11.2.3+12.3.4+13.4.5+…..............
View Solutionसमांतर श्रेढ़ी के N पदों का योग | उदाहरण
View Solutionसमांतर श्रेढ़ी के N पदों का योग पर आधारित प्रश्न
View Solution(1) किसी A.P. के प्रथम 10 पदों का योगफल ज्ञात कीजिए यदि T1=−14 और T5=20.
(ii) किसी A.P. का तीसरा पद 14 और 8वाँ पद 34 है।Sn और S30 ज्ञात कीजिए।
View Solutionसमांतर श्रेढ़ी के N पदों का योग || उदाहरण
View Solutionयदि गुणोत्तर श्रेणी के अन्नत पदों का योगफल S तथा प्रथम पद a है, तो सार्वअनुपात r ज्ञात कीजिए।
View Solutionसमांतर श्रेणी के प्रथम N पदों का योग
View Solutionगुणोत्तर श्रेणी के n पदों का योग|उदाहरण
View SolutionRevision|A.P के प्रथम n पदों का योगफल#!#Boards 2021
View Solution
