k का मान ज्ञात कीजिए यदि समीकरण 2x2−5x+k=0 के मूल समान हैं।
258
18
252
58
The correct Answer is:A
दी समीकरण 2x2−5k+k=0
ax2+bx+c=0 से तुलना करने पर
a=2,b=−5 और c=k
दिए समीकरण के दो बारबार मूल हैं, यदि
D=0
∴D=b2−4ac=0
या (−5)2−4×2×k=0
⇒25−8k=0⇒k=(258)
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - द्विघात समीकरण EXERCISE - प्रश्नावली 4A37videos
द्विघात समीकरण
- BOOK - NOOTAN HINDICHAPTER - द्विघात समीकरण EXERCISE - प्रश्नावली 4B16videos
द्विघात समीकरण
- BOOK - NOOTAN HINDICHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)7videos
दो चर वाले रैखिक समीकरण युग्म
- BOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामितिEXERCISE - बहुविकल्पीय प्रश्न7videos
निर्देशांक ज्यामिति
Similar Questions
निम्नलिखित में से कौन-सी द्विघात समीकरण है?
(i) x2−8x+12=0
(ii) x+1x=5, (iii) x+5x=x2
(iv) x2−5√x+7=0 , (v) x2−5x−√4+4=0, (vi) x2−1x2=4
(vii) 5x2−7x=3x2−7x+3
(viii) 1x2+76x−2=004:37View Solutionपूर्ण वर्ग बनाने की विधि से निम्नलिखित द्विघात समीकरणों के मूल ज्ञात कीजिये:
(i) x2−10x−24=0
(ii) 2x2−7x−39=0
(iii) 5x2+6x−8=002:43View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
02:59View Solutionबिंदु (3, 4) की x-अक्ष से दूरी है :
03:54View Solutionयदि 2x+y=1 तो फलन x2y का उच्चिष्ठ मान ज्ञात कीजिए
02:58View Solutionयदि एक त्रिभुज का क्षेत्रफल 35 वर्ग इकाई तथा शीर्ष (2,-6),(5,4) एवं (k,4) हैं तो k का मान ज्ञात कीजिए ।
01:44View Solutionआकृति के अनुसार यदि ∠BAC=80∘ हो तो ∠BCP का मान ज्ञात कीजिए।
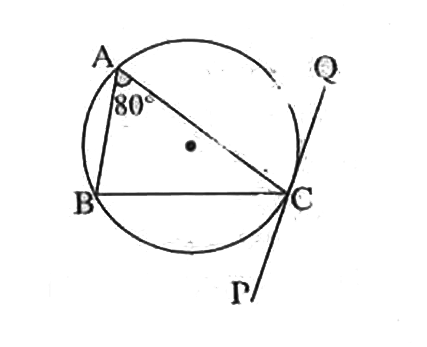 05:00View Solution
05:00View Solutionएक रेख के कार्तीय समीकरण 6x−2=3y+1=2z−2 हैं इसके दिक्-अनुपात ज्ञात कीजिए। साथ ही रेखा का सदिश समीकरण ज्ञात कीजिए।
02:32View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=(2x−1)2+301:36View Solutionनिम्नलिखित फलनों के अधिकतम था निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
sin2x+502:22View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
02:51View Solutionयदि द्विघात समीकरण 81x2+kx+256=0 का एक मूल दूसरे मूल का घन है , तो k का एक मान है
03:13View Solutionयदि समीकरण x2+2mx+m2−2m+6=0 के मूल बराबर हो, तो m का मान होगा।
02:51View Solutionk का वह मान जिसके लिए समीकरण x2−(3k−1)x+2k2+2k−11=0 के मूल समान होगा, है।
02:33View Solutionयदि समीकरण (a2+4a+3)x2+(a2−a−2)x+a(a+1)=0 के दो से अधिक मूल हैं, तो a का मान है
03:12View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
02:23View Solution

