For the reaction A+2B→ products (started with concentration taken in stoichiometric proportion), the experimentally determined rate law is :
−d[A]dt=k√[A]√[B]
The half life time of the reaction would be :
0.693k
0.6931/k
0.693√2k
not defined
The correct Answer is:C
To find the half-life of the reaction A+2B→products with the given rate law:
−d(A)dt=k√(A)√(B)
we will follow these steps:
Step 1: Understand the stoichiometric proportions
Since the reaction starts with concentrations in stoichiometric proportions, we can assume that initially, the concentration of A is (A)0 and the concentration of B is 2(A)0 (because it requires 2 moles of B for every mole of A).
Step 2: Write the rate law in terms of concentration
From the rate law, we have:
−d(A)dt=k√(A)√(B)=k√(A)√2(A)0−(A)
Step 3: Substitute (B) in terms of (A)
Since (B)=2(A)0−(A), we can substitute this into the rate equation:
−d(A)dt=k√(A)√2(A)0−(A)
Step 4: Rearrange the equation
Rearranging gives us:
d(A)√(A)√2(A)0−(A)=−kdt
Step 5: Integrate the equation
Integrate both sides. The left side requires a suitable substitution or recognition of the integral form. The limits for (A) will go from (A)0 to (A)0/2 for half-life.
Step 6: Find the expression for half-life
After integration, we find that the half-life t1/2 can be expressed as:
t1/2=0.693k√2(A)0
Final Expression
Thus, the half-life of the reaction is:
t1/2=0.693k√2(A)0
Since the reaction starts with concentrations in stoichiometric proportions, we can assume that initially, the concentration of A is (A)0 and the concentration of B is 2(A)0 (because it requires 2 moles of B for every mole of A).
From the rate law, we have:
Since (B)=2(A)0−(A), we can substitute this into the rate equation:
Rearranging gives us:
Integrate both sides. The left side requires a suitable substitution or recognition of the integral form. The limits for (A) will go from (A)0 to (A)0/2 for half-life.
After integration, we find that the half-life t1/2 can be expressed as:
Thus, the half-life of the reaction is:
Topper's Solved these Questions
- CHEMICAL KINETICSBook:A2ZChapter:CHEMICAL KINETICSExercise:Initial Rate Method And Ostwaid Method
Explore 18 Videos
- CHEMICAL KINETICSBook:A2ZChapter:CHEMICAL KINETICSExercise:Arrhenius Equation, Effect Of Temprature And Effect Of Catalysts
Explore 35 Videos
- CHEMICAL KINETICSBook:A2ZChapter:CHEMICAL KINETICSExercise:Rate Law, Law Of Mass Action, Order Of The Reaction, And Molecularity
Explore 48 Videos
- BIOMOLECULESBook:A2ZChapter:BIOMOLECULESExercise:Section D - Chapter End Test
Explore 30 Videos
- COORDINATION COMPOUNDSBook:A2ZChapter:COORDINATION COMPOUNDSExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
Knowledge Check
For the reaction 2A+B→C with the rate low d[C]dt=k[A]1[B]−1 and started with A and B in stoichiometric proportion.Which is/are true ?
Aunit of k is Ms−1B[A],[B] and [C] all will be linear functions of timeC[C]=2ktD[C]=ktFor the reaction A+B→C+D The variation of the concentration of the products is given by the curve
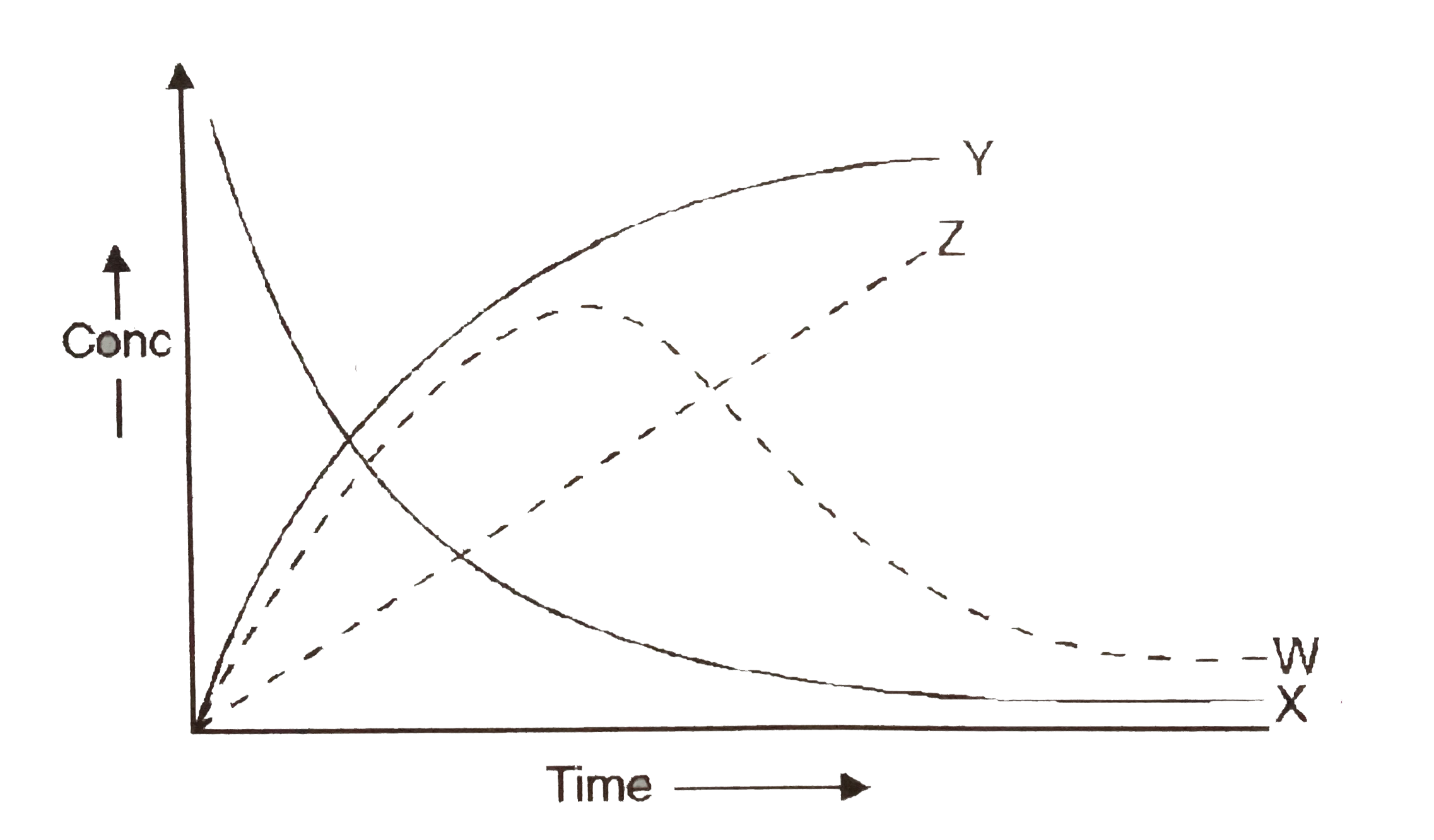 AXBYCWDZ
AXBYCWDZFor a hypothetical reaction: A+B→ Products, the rate law is r=k[A][B]0. The order of reaction is
A0B1C2D3
The rate of change of concentration of (A) for reaction A→B is given by
−d[A]dt=k[A]1/3
Derive expression for half-life period of the reaction.
View SolutionFor the reaction A+ B rightarrowproduct , the folowing initial rates were obtained at various given initial concentrations:

Determine the half - life period.
View SolutionFor a reation: A→ Product,
rate law is −d[A]dt=K[A]0.
The concentration of A left after time t when t=1K is:
View SolutionFor the reaction A+2B→2C+D, the concentration of A is kept constant and that of B is tripled, the rate of reaction will become
View SolutionFor a reation: A→ Product,
rate law is −d[A]dt=K[A]0.
The concentration of A left after time t when t=1K is:
View Solution

