निम्नलिखित व्यंजकों को एकपदी, द्विपद और त्रिपद के रूप में वर्गीकृत कीजिएः
(i) 4y−7z (ii) y2 (iii) x+y−xy (iv) 100 (v) ab−a−b (vi) 5−3t (vii) 4p2q−4pq2 (viii) 7mn (ix) z2−3z+8 (x) a2+b2 (xi) z2+z (xii) 1+x+x2
The correct Answer is:(i) द्विपद (ii) एकपदी (iii) त्रिपद (iv) त्रिपद (v) त्रिपद (vi) द्विपद (vii) द्विपद (viii) एकपदी (ix) त्रिपद (x) द्विपद (xi) द्विपद (xii) त्रिपद
Step by step video, text & image solution for निम्नलिखित व्यंजकों को एकपदी, द्विपद और त्रिपद के रूप में वर्गीकृत कीजिएः (i) 4y-7z (ii) y^(2) (iii) x+y-xy (iv) 100 (v) ab-a-b (vi) 5-3t (vii) 4p^(2)q-4pq^(2) (viii) 7mn (ix) z^(2)-3z+8 (x) a^(2)+b^(2) (xi) z^(2)+z (xii) 1+x+x^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- बीजीय व्यंजक BOOK - NCERT HINDICHAPTER - बीजीय व्यंजक EXERCISE - प्रश्नावली 12.2
6 Videos
- बीजीय व्यंजक BOOK - NCERT HINDICHAPTER - बीजीय व्यंजक EXERCISE - प्रश्नावली 12.3
10 Videos
- बीजीय व्यंजक BOOK - NCERT HINDICHAPTER - बीजीय व्यंजक EXERCISE - इन्हें कीजिए
3 Videos
- प्रायोगिक ज्यामिति BOOK - NCERT HINDICHAPTER - प्रायोगिक ज्यामिति EXERCISE - प्रश्नावली 10.4
3 Videos
- भिन्न एवं दशमलव BOOK - NCERT HINDICHAPTER - भिन्न एवं दशमलव EXERCISE - प्रश्नावली 2.7
6 Videos
Similar Questions
समान पदों को संयोजित (मिला) करके सरल कीजिए
(i) 21b−32+7b−20b
(ii) −z2+13z2−5z+7z3−15z
(iii) p−(p−q)−q−(q−p)
(iv) 3a−2b−ab−(a−b+ab)+3ab+b−a
(v) 5x2−5x2+3yx2−3y2+x2+y2+8xy2−3y2
(vi) (3y2+5y−4)−(8y−y2−4)
View Solutionयदि m=2 है तो निम्नलिखित के मान ज्ञात कीजिए।
(i) m−2 (ii) 3m−5 (iii) 9−5m
3m2−2m−7 (v) 5m24
View Solutionमाचिस की तीलियों, दांत साफ करने की सीकों या सरकंडों के बराबर लंबाई के टुकड़ों के छोटे रेखाखंडों को लीजिए। उन्हें आकृतियों में दर्शाए अनुसार प्रतिरूपों में जोड़िएः आकृति में बने पैटर्न को देखिए। इसमें चार रेखाओं से बने आकार की पुरावृत्ति हो रही है जैसा कि आप देख सकते हैं कि एक आकार को बनाने के लिए चार रेखाखंडों की आवश्यकता होती है दो आकारों के लिए 7 तीन आकारों के लिए 10 इत्यादि रेखाखंडों की आवश्यकता होती है। यदिो आकारों की संख्या n हो तो उन्हें बनाने के लिए आवश्यक रेखाखंडों की संख्या (3n+1) होगी। आप इसकी सत्यता की जांच n=1,2,3,10………. इत्यादि लेकर कर सकते हैं। यदि बनाए गए आकारों की संख्या 3 है तो आवश्यक रेखाखंडों की संख्या 3×3+1=10 होती जैसाकि आकृति से भी देखा जा सकता है।
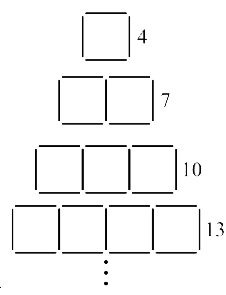
View Solutionसमकोण ΔPOR की रचना कीजिए , जहाँ m∠Q=90∘, और QR=8cm , PR=10 cm
View Solutionज्ञात कीजिए :
(i)0.4÷2(ii)0.35÷5(iii)2.48÷4(iv)65.4÷6(v)651.2÷4(vi)14.49÷7(vii)3.96÷4(viii)0.80÷5
View SolutionEvaluate each of the following algebraic expressions for x=1, y=−1,z=2, a=−2, b=1, c=−2: (i) ax+by+cz (ii) ax2+by2−cz2 (iii) axy+byz+cxy
View Solutiony2+yz+z2(x−y)(x−z)+z2+zx+x2(y−z)(y−x)+x2+xy+y2(z−x)(z−y)
View SolutionLet x,y,z in R and 2x+y+3z=20 then min.value of x^(2)+4y^(2)+z^(2) will be
View SolutionFactorise the following : (i)9a2−b2 (ii)81x3−x (iii)x3−49xy2 (iv)a2−(b−c)2 (v)(x−y)3−x+y (vi)x2y2+1−x2−y2 (vii)25(a+b)2−49(a−b)2 (viii)xy5−x5y (ix)x8−256 (x)x8−81y8
View Solutionनिम्निलिखित रेखा युग्मों के मध्य कोण ज्ञात कीजिये-
(i) x+2−2=y−24=z−13 तथा x+13=y−3−2=z−14
(ii) x+3−1=y−12=z+4−3 तथा x−1−2=y+2−3=z−11
(iii) x−22=y−15=z+3−3 और x+2−1=y−48=z−54
(iv) x2=y2=z1 और x−54=y−21=z−38
View SolutionProve that ∣∣ ∣ ∣∣x2x2−(y−z)2yzy2y2−(z−x)2zxz2z2−(x−y)2xy∣∣ ∣ ∣∣
=(x−y)(y−z)(z−x)(x+y+z)(x2+y2+z2)
View Solutionनिम्नलिखित के गुणनखण्ड कीजिए :
(i) 9a2−b2 (ii) 81x3−x (iii) x2−49xy2 (iv) a2−(b−c)2
(v) (x−y)3−x+y (vi) x2y2+1−x2−y2 (vii) 25(a+b)2−49(a−b)2 (viii) xy5−x5y
(ix) x8−256 (x) x8−81y8
View Solutionनिम्नलिखित समांतर रेखाओं के बीच की दूरी ज्ञात कीजिएः
x−12=y−23=z−34 और x−24=y−36=z−48.
View SolutionWrite the coefficient of
(i) x in 13x
(ii) y in - 5y
(iii) a in 6ab
(iv) z in - 7xz
(v) p in - 2 pqr
(vi) y2 in 8xy2z
(vii) x3 in x3
(viii) x2 in −x2
View Solutiona=x2+xy+y2,b=y2+yz+z2,c=z2+xz+x2 হলে (x−y)a+(y−z)b+(z−x)c -এর মান নির্ণয় করো |
View Solution
