The effective cross section of a uranium nucleus corresponding to the scattering of monoenergetic alpha particles with an the angular interval from 90∘ to 180∘ is equal to Δσ=0.50kb. Find ,
(a) the energy of alpha particles,
(b) the differntial cross section of scattering dsingma/dΩ(kb/sr) coresponding to the angle θ=60∘
(a) From the previous formula
Δσ=(Ze2(4πε0)2T)2πcot2θ02
or T=Ze24πε0cotθ02√πΔσ Substituting the values with Z=79 we get (θ0=90∘)
T=0.903MeV
The differential scattering cross section is
dsingmadΩ=Ccosec4θ2
where Δσ(θ>θ0)=4πCcot2θ02 Thus from the given data
C=5004πb=39.79b/sr
So dσdΩ(θ=60∘)=39.79×16b/sr=0.637kb/sr
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Wave Properties Of Particle
48 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Find the effective corss section of a uranium nucleus corresponding to the scattering ofalpha particles with kinetic energy T=1.5MeV through the angles exceeding θ0=60∘.
View SolutionA narrow beam of alpha particles with kinetic energy T=600keV falls normally on a golden foil incorporating n=1.1.1019 nuclei/cm2. Find the fraction of alpha particles scattered thtough the angles θ<θ0=20∘
View Solution
Knowledge Check
In alpha-particle scattering experiment, the perpendicular distance(b) of initial velocity vector of the the alpha-particle from the centre of nucleus is equal to (where E is initial kinetic energy of alpha-particle) (##AAK_MCP_38_NEET_PHY_E38_020_Q01##)
AZe2sin2(θ2)4πε0EBZe2cot(θ2)4πε0ECZe2cos(θ2)4πε0EDZ2e2Esin4(θ2)4πε0At the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by α-particles from a polonium source. It was expected that α-particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of α-particles is proportional to target thickness and is inversely proportional to the fourth power of sin(θ2), where,θ is scattering angle. Distance of closest approach may be calculated as:
rmin=Z1Z2e24πε0K
where, K=kinetic energy of α-particles.
Q. Which of the following quantities will be zero for alpha particles at the point of closest approach to the gold atom, in Rutherford's scattering of alpha particles?AAccelerationBKinetic energyCPotential energyDElectrical energyAt the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by α-particles from a polonium source. It was expected that α-particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of α-particles is proportional to target thickness and is inversely proportional to the fourth power of sin(θ2), where,θ is scattering angle. Distance of closest approach may be calculated as:
rmin=Z1Z2e24πε0K
where, K=kinetic energy of α-particles.
Q. Rutherford's scattering formula fails for vary small scattering angles because:AThe gold foil is very thinBthe kinetic energy of α-particle is very highCThe full nuclear charge of the target atom is partially screened by its electronDThere is strong repulsive force between the α-particles and nucleus of the target.
An alpha particle with kinetic energy T=0.50MeV is deflected through an angle of θ=90∘ by Coulomb field of a stationary Hg nucleus. Find:
(a) the least curvature radius of its trajectory,
(b) the minimum approach distance between the particle and the nucleus.
View SolutionAn alpha - particle of 5MeV energy strikes with a nucleus of uranium at stationary at an scattering angle of 180o .The nearest distance up to which alpha - particle reaches the nucleus will be of the order of
View SolutionRutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:
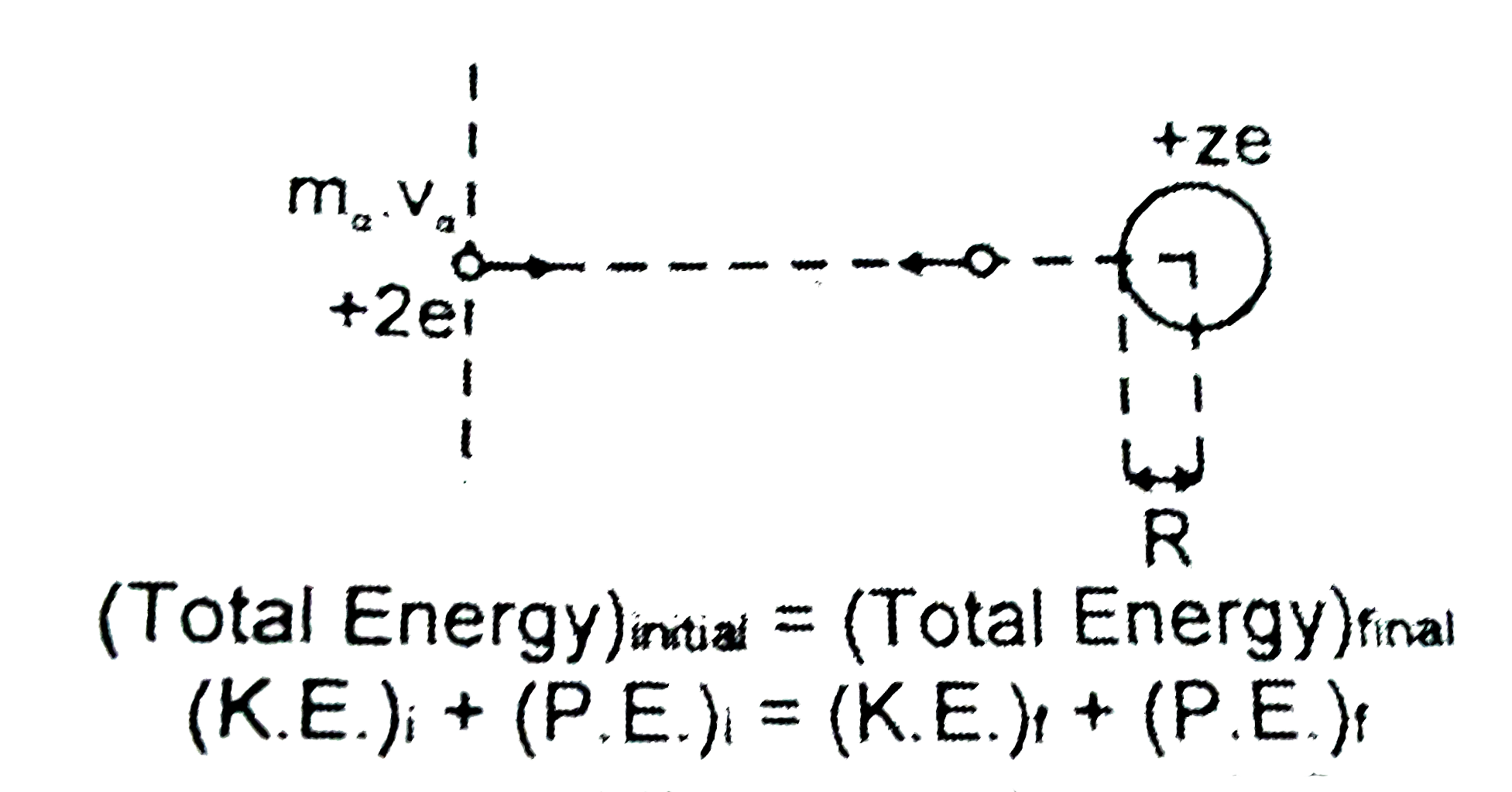
(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :
View SolutionAt the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by α-particles from a polonium source. It was expected that α-particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of α-particles is proportional to target thickness and is inversely proportional to the fourth power of sin(θ2), where,θ is scattering angle. Distance of closest approach may be calculated as:
rmin=Z1Z2e24πε0K
where, K=kinetic energy of α-particles.
Q. Rutherford's α-particle scattering led to the conclusion that:
View SolutionAt the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by α-particles from a polonium source. It was expected that α-particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of α-particles is proportional to target thickness and is inversely proportional to the fourth power of sin(θ2), where,θ is scattering angle. Distance of closest approach may be calculated as:
rmin=Z1Z2e24πε0K
where, K=kinetic energy of α-particles.
Q. Alpha particles that come closer to the nuclei:
View Solution
