Find the lowest values o fthe kinetic energy of an electron and a proton causing the emergence of Cherenkov's radiation in a medium with refractive index n=1.60. For what particles is this minimum value of kinetic enegry equal to Tmin=29.6MeV?
We must have
V≥cn=31.6×108m/s or Vc≥11.6
For electrons this means a K.E. greater than
Te≥mec2√1−(11.6)2−mec2=mec2[n√n2−1−1]
=0.511⎡⎢
⎢
⎢
⎢⎣1√1(11.6)2−1⎤⎥
⎥
⎥
⎥⎦ using mec2=0.511MeV=0.144MeV
For protons with mPc2=938MeV
TP≥938⎡⎢
⎢
⎢
⎢⎣1√1−(11.6)2−1⎤⎥
⎥
⎥
⎥⎦=264MeV=0.264GeV
Also Tmin=29.6MeV=mc2⎡⎢
⎢
⎢
⎢⎣1√1−(11.6)2−1⎤⎥
⎥
⎥
⎥⎦
Then mc2=105.3MeV. This is very nearly the mass of means.
Topper's Solved these Questions
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Thermal Equation
Explore 47 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Dispersion And Absorption Of Light
Explore 24 Videos
- MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:MECHANICSExercise:Mechanics Problems
Explore 92 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
Similar Questions
Find the kinetic enegry of electrons emitting light in a medium with refractive index n=1.50 at an angle θ=30∘ to their propagation direction.
View SolutionUp to what values of kinetic energy does the period of revolution of an electron and a proton in a uniform magnetic field exceed that at non-relativistic velocities by η=1.0%
View SolutionA moving neutron collides with stationary H-atom in ground state. As a result it excites and then de-excites. The corresponding radiation fail on a surface having work function σ. The minimum value of required kinetic energy for neutron is E0 and possible minimum value of de-Broglie wavelength of emitted photoelectrons is λ0. If the neutron hits stationary (He)+ ion instead of stationary (H) atom, then the minimum value of kinetic energy for neutron is E1 and the value of energy. transferred from neutron to H-atom is xE0y. Find (xy).
View SolutionFind the energy of the reaction .14N(α,p).17O, if the kinetic energy of the incoming α-particle is Tα=4.0MeV & the proton outgoing at an angle θ=60∘ to the motion direction of the α-particle has a kinetic energy Tp=2.09MeV.
View SolutionFind the enrgy of the reaction N14(α,p)O17 if the kinetic enrgy of the incoming alpha-pariticle is Tα=40MeV and the proton outgoing at an angle θ=60∘ to the motion direction of the alpha-particle has a kinetic energy TP=2.09MeV.
View SolutionA single electron orbits around a stationary nucless of charge +Ze where Z is a constant and e is the magnitude of electronic charge ,if respuires 47.2 e

is excite the electron from the second bohr orbit to the third bohr orbit
a. Find the value of Z
b. Find the energy required to the electron from n=3 ton=4
c. Find the wavelength of radiation to remove the electron from the second bohr orbit to infinity
d. Find the kinetic energy potential energy and angular momentum of the electron in the first orbit
Find the ionination energy of above electron system in electronvalt.
View SolutionProtons are accelerated in a cyclotron so that the maximum curvature radius of their trajectory is equal to r=50cm. Find:
(a) the kinetic energy of the protons when the acceleration is completed if the magnetic induction in the cyclotron is B=1.0T,
(b) the minimum frequency of the cycloroton's oscillator at which the kinetic energy of the protons amounts to T=20MeV by the end of accelearation.
View SolutionProve that a charged particle entering a strong uniform magnetic field experiences specular reflection, if its speed is below some limiting value (the "magnetic mirror" principle, Fig. 28.20). Find the kinetic energy of the electrons which experience specular reflection, if the electron beam is perpendicular to the magnetic mirror" magnetic field with an induction B= 0.1 T is established in a large region, the thickness of the magnetic mirror" is d= 10 cm.
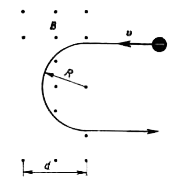
View SolutionA stationary neutral particle disintegrated into a proton with kinetic energy T=5.3MeV and a negative pion. Find the mass of that particle. What is its name.
View SolutionFind the Q value of the reaction
N14+α→O17+P
The mass of are, respectively,14.00307u,4.00260u, and 16.99913u. Find the total kinetic energy of the products if the striking α particles has the minimum kinetic energy required to initiate the reaction .
View Solution

