A source of sinusoidal emf with constant voltage is connected in series with an oscillating circuit with quality factor $Q = 100$ . At a certain frequency of the external voltage the heat power generated in the circuit reached the maximum value. How much $($ in per cent $)$ should this frequency be shifted to decrease the power generated $n = 2.0$ times ?

Video Solution

Text Solution

Verified by Experts

$P = \frac{V^{2} R}{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
At resonance $X_{L} = X_{C} \Rightarrow ω_{0} = \frac{1}{\sqrt{L C}}$
Power generated will decrease $n$ times when
$(X_{L} - X_{C}) - {(ω L - \frac{1}{ω C})}^{2} = (n - 1) R^{2}$
or $ω - \frac{ω_{0}^{2}}{ω} = \pm \sqrt{n - 1} \frac{R}{L} = \pm \sqrt{n - 1} 2 β$
Thus $ω ¯ ¯¯¯ ¯ + 2 \sqrt{n - 1} β ω - ω_{0}^{2} = 0$
${(ω ¯ ¯¯¯ ¯ + \sqrt{n - 1} β)}^{2} = ω_{0}^{2} + (n - 1) β^{2}$
or $\frac{ω}{ω_{0} = \sqrt{1 + (n - 1) β^{2} / ω_{0}^{2}}} \pm \sqrt{n - 1} β / ω_{0}$
$($ taking only the positive sign in the first term to ensure positive valur for $\frac{ω}{ω_{0}} .)$
Now $Q = \frac{ω}{2 β} = \frac{1}{2} \sqrt{{(\frac{ω_{0}}{β})}^{2} - 1}$
$\frac{ω_{0}}{β} = \sqrt{1 + 4 Q^{2}}$
Thus $\frac{ω}{ω_{0}} = \sqrt{1 + \frac{n - 1}{(1 + 4 Q)}} \pm \sqrt{n - 1} / \sqrt{1 + 4 Q}$
For large $Q$
$∣ ∣ ∣ \frac{ω - ω_{0}}{ω_{0}} ∣ ∣ ∣ = \frac{\sqrt{e n - 1}}{2 Q} - \frac{\sqrt{e n - 1}}{2 Q} \times 100 % = 0.5 %$

Updated on:21/07/2023

An a.c. source is connected across an LCR series circuit with $L = 100 m H, C = 0.1 μ F$ and $R = 50 Ω$ . The frequency of ac to make the power factor of the circuit, unity is
A $\frac{10^{4}}{2 π} H z$
B $\frac{10^{3}}{2 π} H z$
C $\frac{10^{- 4}}{2 π} H z$
D $\frac{10^{- 3}}{2 π} H z$
Time constant of the given circuit is $τ$ If the battery is replaced by an ac source having voltage $V = V_{0} cos ω t$ , power factor or the circuit will be

A $ω T$
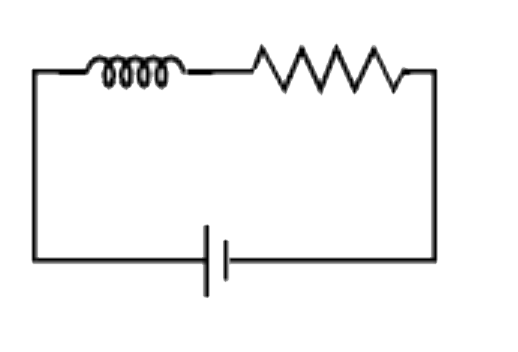B $\frac{1}{\sqrt{1 + {(ω τ)}^{2}}}$
C $\sqrt{1 - {(ω τ)}^{2}}$
DNone
An ac generator $G$ with an adjustable frequency of oscillation is used in the circuit, as shown.

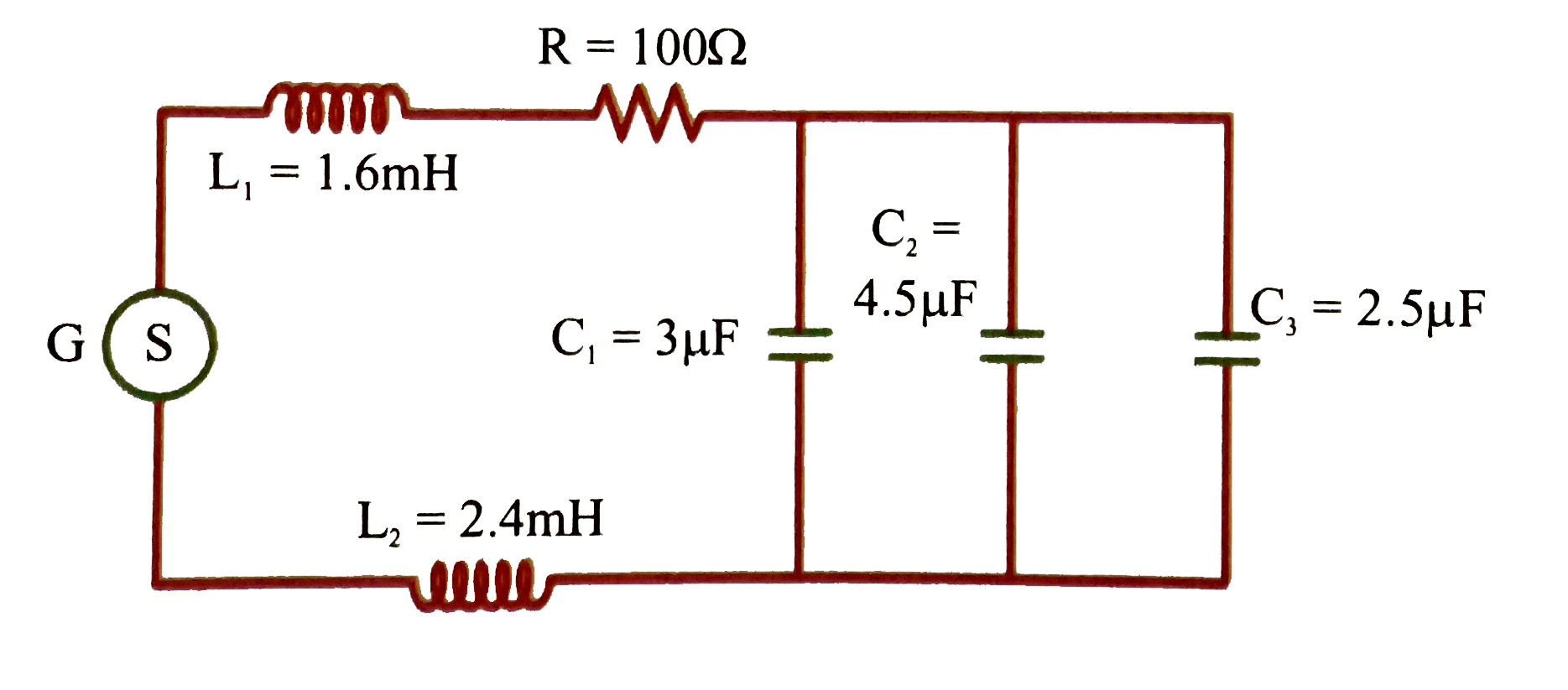
If the ac source $G$ is $100 V$ rating at resonant frequency of the circuit, then average power supplied by the source is
A $50 W$
B $100 W$
C $500 W$
D $1000 W$