Find the internal pressure pi of a liquid if its density ρ and specific latent heat of vaporization q are known. The heat q is assumed to be equal to the work performed against the forces of the internal pressure, and the liquid obeys the Van der Waals equation. Calculate pi in water.
The internal pressure being aV2, the work done in condensation is
∫VsVlaV2dV=aVl−aVg≈aVl
This by assumption is Mq,M being the molecular weight and Vl,Vg being the molae volumes of the liquid and gas.
Thus pl=aV2l=MqVl=ρq
where ρ is the density of the liquid . For water pi≈3.3×1013atm.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Liquids Capillary Effects
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
As a result of heating a mole of an ideal gas at constant pressure by 72∘C, a heat flow by an amount 1600 joules takes place. Find the work performed by the gas, ther increment of its internal energy, and the value of γ.
View SolutionFind the pressure of saturated vapour as a function of temperature p(τ) if a temperature T0 its pressure equals p0. Assume that : the specific latent heat of vaporization q is independent of T, the specific volume of liquid is negligible as compared to that of vapour, saturated vapour obeys the equation of state for an ideal gas. Investigate under what conditions these assumptions are permissible.
View SolutionAs a result of the isobaric heating by ΔT=72K, one mole of a certain ideal gas obtain an amount of heat Q=1.6kJ. Find the work performed by the gas, the increment of its internal energy and γ.
View SolutionAs a result of the isobaric heating by ΔT=72 K one mole of a certain ideal gas obtains an amount of heat Q = 1.60 kJ. Find the work performed by the gas, the increment of its internal energy, and the value of γ=Cp/Cv
View SolutionOne gram of water (1cm3) becomes 1671 cm3 of steam at a pressure of 1 atm. The latent heat of vaporization at this pressure is 2256 J/g. Calculate the external work and the increase in internal energy.
View SolutionFind the change in internal energy of a gas when (i) it absorbs 80 calorie of heat and performs work equal to 170 Joule (ii) it absorbs 20 calorie of heat and work equal to 55 Joule is performed on it.
View SolutionA cylinder vessel containing a liquid of density ρ is closed by a smooth piston of mass m as shown. If atmospheric pressure is P0, radius of cylinder is r and height of liquid is h. Find
(a) Pressure of liquid just below the piston
(b) force at bottom of cylinder.
 .
.
View SolutionA liquid having surface tension T and density ρ is in contact with a vertical solid wall. The liquid surface gets curved as shown in the figure. At the bottom the liquid surface is flat. The atmospheric pressure is Po.
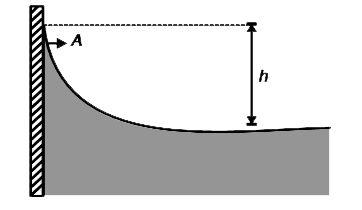
(i) Find the pressure in the liquid at the top of the meniscus (i.e. at A)
(ii) Calculate the difference in height (h) between the bottom and top of the meniscus.
View SolutionIf an additional pressure Δp of a saturated vapour over a convex spherical surface of a liquid is considerably less than the vapour pressure over a plane surface, then Δp=(ρv/ρl)2α/r, where ρv and ρl) are the densities of the vapour and the liquid, α is the surface tension, and r is the radius of curvature of the surface. Using this formula, find the diameter of water droplets at which the saturated vapour pressure exceeds the vapour pressure over the plane surface by η=1.0% at a temperature t=27∘C. The vapour is assumed to be an ideal gas.
View SolutionOne mole of an ideal gas is heated at constant pressure so that its temperature rises by ΔT= 72 K. In The heat supplied is Q=1.6 kJ, find the change in its internal energy and the work done by the gas.
View Solution