Refer to the arrangement of charges in Fig and a Gaussian surface of radius with at the centre. Then
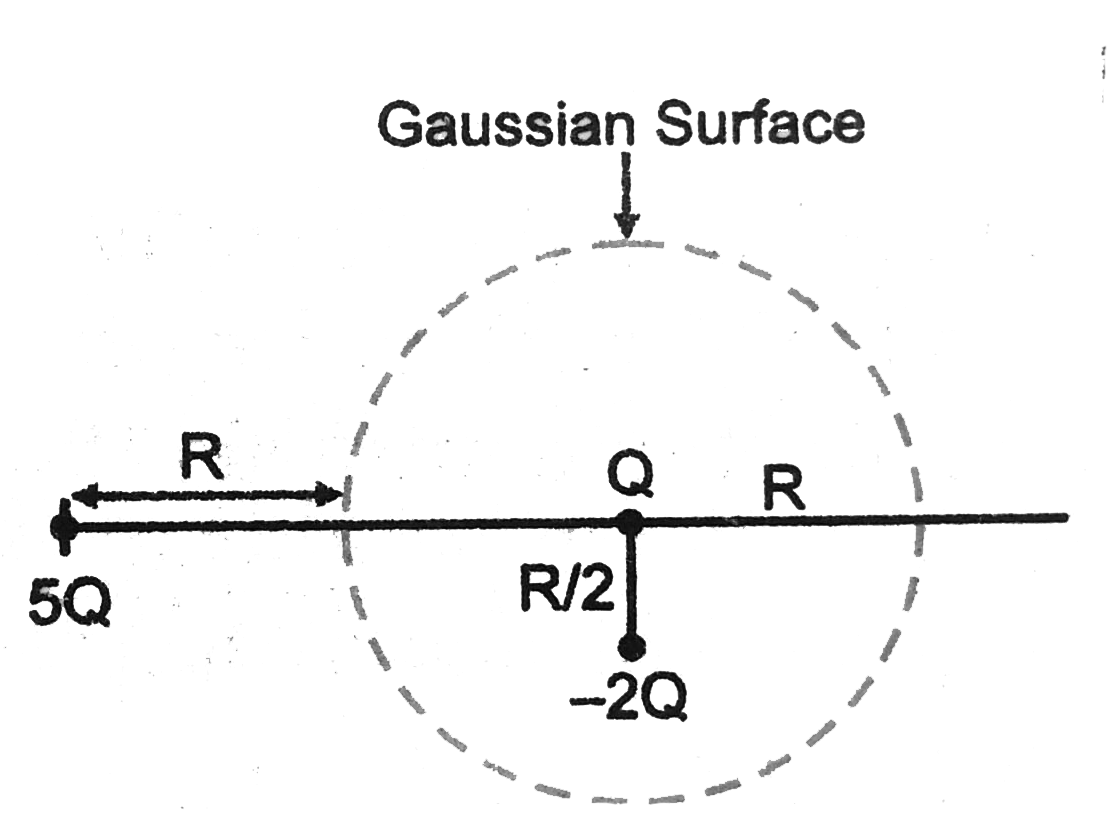
total flux through the surface of the sphere is
field on the surface of the sphere si
flux through the surface of sphere due to is zero.
field on the surface of sphere due to is same everywhere
The correct Answer is:A, C
In Fig, charge enclosed by the Gaussain surface , Therefore, as per Gauus's theorem, total flux through the given surface Choices (a) and ( c) are correct.
Topper's Solved these Questions
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:FILL IN THE BLANKS
Explore 8 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:PROBLEMS FOR PRACTICE
Explore 8 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:VALUE BASED QUESTIONS
Explore 7 Videos
- ELECTRONIC DEVICESBook:PRADEEPChapter:ELECTRONIC DEVICESExercise:Fill in the Blanks
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
Knowledge Check
The work done in carrying a charge q once around a circle of radius r with a charge Q placed at the centre centre will be
AQq4πε0r2BQq4πε0rCzeroDQq24πε0rThe work done in carrying a charge q once around a circle of radius r with a charge Q placed at the centre centre will be
AQq4πε0r2BQq4πε0rCzeroDQq24πε0rThe work done in carrying a charge Q1 once round a circle of radius R with a charge Q2 at the centre is
AQ1Q24π∈0R2BzeroCQ1Q24π∈0RDinfinite
A solid insulating sphere of radius a carries a net positive charge 3Q, uniformly distributed throughout its volume. Concentric with this sphere is a conducting spherical shell with inner radius b and outer radius c and having a net charge -Q, as shown in figure

a. Consider a spherical Gaussian surface of radius rgtc, the net charge enclosed by this surface is .............
b. The direction of the electric field rgtc is .............
c. The electric field at rgtc is ............... .
d. The electric field in the region with radius r, which cgtrgtb, is ...............
e. Consider a spherical Gaussian surface of radius r, where c>r>b, the net charge enclosed by this surface is ................ .
f. Consider a spherical Gaussian surface of radius r, whereb>r>a, the net charge enclosed by this surface is ................. .
g. The electric field in the region b>r>a is ................ .
h. Consider a spherical Gaussian surface of radius r<a. Find an expression for the net charge Q(r) enclosed by this surface as a function of r. Note that the charge inside the surface is less than 3Q.
i. The electric field in the region r<a is ................. .
j. The charge on the inner surface of the conducting shell is .......... .
k. The charge on the outer surface of the conducting shell is .............. .
l. Make a plot of the magnitude of the electric field versus r.
View SolutionA charge of 8.85C is placed at the centre of a spherical Gaussian surface of radius 5cm .The electric flux through the surface ..
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surfance of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surfce is .

View Solutionq1,q2,q3 and q4 are point charges located at point as shown in the figure and S is a spherical Gaussian surface of radius R. Which of the following is true according to the Gauss's law

View SolutionAssertion:- In a given situation of arrangement of charges, an extra charge is placed outside the Gaussion surface. In the Gauss Theroem
∮→Ed→s=Q∈ε0Q∈ remains unchanged whereas electric field →E at the site of the element is changed.
Reason:- Electric field →E at any point on the Gaussian surface is due to inside charge only.
View Solution

