Two point charges q and −2q are kept 'd' distance apart. Find the location of the point relative to charge q at which potential due to the system of charges is zero.
The correct Answer is:d/3 from charge q
To find the location of the point relative to charge q at which the potential due to the system of charges is zero, we can follow these steps:
Step 1: Understand the Setup
We have two point charges:
- Charge q located at point A.
- Charge −2q located at point B, which is d distance away from charge q.
Step 2: Define the Point of Interest
Let’s denote the point where the potential is zero as point P. Let the distance from charge q to point P be x. Consequently, the distance from charge −2q to point P will be d−x.
Step 3: Write the Expression for Electric Potential
The electric potential V at point P due to both charges can be expressed as:
VP=Vq+V−2q
Where:
- Vq=14πϵ0⋅qx (Potential due to charge q)
- V−2q=14πϵ0⋅−2qd−x (Potential due to charge −2q)
Step 4: Set the Total Potential to Zero
To find the point where the total potential is zero, we set the equation:
14πϵ0⋅qx+14πϵ0⋅−2qd−x=0
We can simplify this by multiplying through by 4πϵ0:
qx−2qd−x=0
Step 5: Solve for x
Now, we can rearrange the equation:
qx=2qd−x
Cancelling q (assuming q≠0):
1x=2d−x
Cross-multiplying gives:
d−x=2x
Rearranging terms results in:
d=3x
Thus, we find:
x=d3
Step 6: Determine the Location Relative to Charge q
The point P where the potential is zero is located at a distance of d3 from charge q.
Final Answer
The location of the point relative to charge q at which the potential due to the system of charges is zero is d3.
---
We have two point charges:
- Charge q located at point A.
- Charge −2q located at point B, which is d distance away from charge q.
Let’s denote the point where the potential is zero as point P. Let the distance from charge q to point P be x. Consequently, the distance from charge −2q to point P will be d−x.
The electric potential V at point P due to both charges can be expressed as:
VP=Vq+V−2q
Where:
- Vq=14πϵ0⋅qx (Potential due to charge q)
- V−2q=14πϵ0⋅−2qd−x (Potential due to charge −2q)
To find the point where the total potential is zero, we set the equation:
14πϵ0⋅qx+14πϵ0⋅−2qd−x=0
We can simplify this by multiplying through by 4πϵ0:
qx−2qd−x=0
Now, we can rearrange the equation:
qx=2qd−x
Cancelling q (assuming q≠0):
1x=2d−x
Cross-multiplying gives:
d−x=2x
Rearranging terms results in:
d=3x
Thus, we find:
x=d3
The point P where the potential is zero is located at a distance of d3 from charge q.
The location of the point relative to charge q at which the potential due to the system of charges is zero is d3.
Topper's Solved these Questions
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:FILL IN THE BLANKS
Explore 8 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:PROBLEMS FOR PRACTICE
Explore 8 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:VALUE BASED QUESTIONS
Explore 7 Videos
- ELECTRONIC DEVICESBook:PRADEEPChapter:ELECTRONIC DEVICESExercise:Fill in the Blanks
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
Two charge _q and -3q are placed at a distance of 1 m apart.Find out the points on the line joing two charges, where electric potential is zero.
View SolutionCharges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
View Solution
Knowledge Check
Two point charges Q and −Q/4 are separated by a distance X. Then
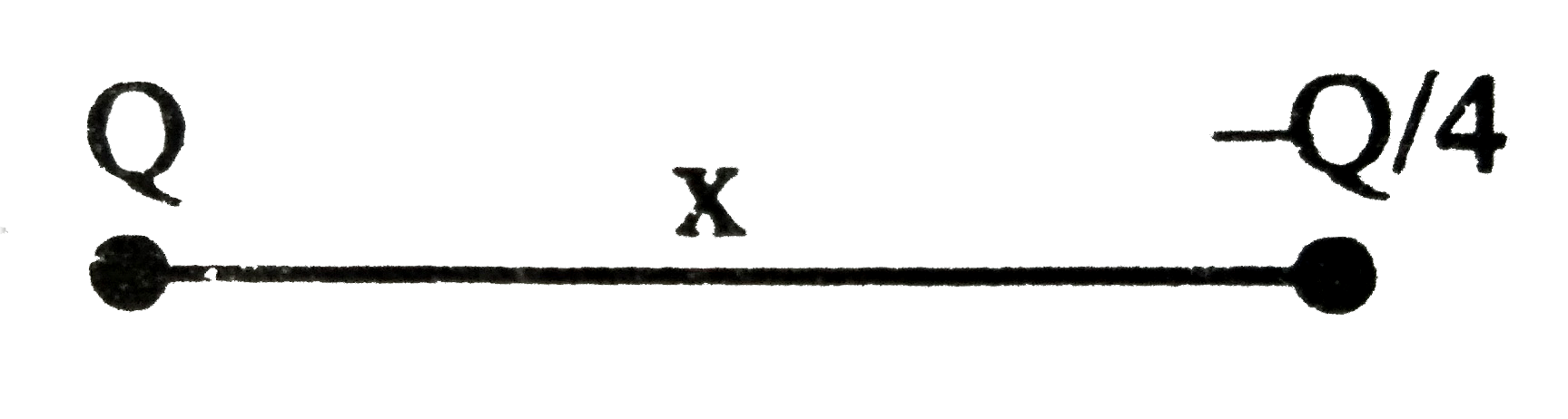 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.Two point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
A(a) L4B(b) 2LC(c) 4LD(d) 8LTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
Auknknown charge is −4q/9Bunknown charge is −9q/4Cit should be at (x/3)from smaller chargge between themDnone of these
Two point charges q1, and q2 are kept at a distance of r12 in air. Deduce the expression for the electrostatic potential energy of this system.
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View SolutionTwo points charges q and -2q are placed some distance d apart. If the electric field at the location of q is E, that at the location of -2q is
View SolutionTwo point charges +8q and -2q located at x =0 and x=L respectively . The location of a point on the x-axis at which the net electric field due to these two point charges is zero is.
View Solution