Two charges of −4μCand+4μC are placed at the points A(1,0,4)andB(2,−1,5) location in an electric field →E=0.20ˆiV/cm. Calculate the torque acting on the dipole.
The correct Answer is:1.13×10−4N−m
To calculate the torque acting on the dipole formed by two charges of -4 µC and +4µC, we will follow these steps:
Step 1: Identify the Position Vectors
The position vectors of the charges are given as:
- Charge −4µC at point A (1, 0, 4):
\(
\vec{r_1} = 1\hat{i} + 0\hat{j} + 4\hat{k}
\)
- Charge +4µC at point B (2, -1, 5):
\(
\vec{r_2} = 2\hat{i} - 1\hat{j} + 5\hat{k}
\)
Step 2: Calculate the Dipole Moment
The dipole moment \(\vec{p}\) is given by the formula:
\(
\vec{p} = q \cdot \vec{d}
\)
where \(\vec{d}\) is the displacement vector from the negative charge to the positive charge.
First, calculate \(\vec{d}\):
\(
\vec{d} = \vec{r_2} - \vec{r_1} = (2\hat{i} - 1\hat{j} + 5\hat{k}) - (1\hat{i} + 0\hat{j} + 4\hat{k}) = (2-1)\hat{i} + (-1-0)\hat{j} + (5-4)\hat{k} = 1\hat{i} - 1\hat{j} + 1\hat{k}
\)
Now, substituting \(q = 4 \times 10^{-6} C\):
\(
\vec{p} = 4 \times 10^{-6} \cdot (1\hat{i} - 1\hat{j} + 1\hat{k}) = 4 \times 10^{-6}\hat{i} - 4 \times 10^{-6}\hat{j} + 4 \times 10^{-6}\hat{k}
\)
Step 3: Electric Field Vector
The electric field vector is given as:
\(
\vec{E} = 0.20\hat{i} \text{ V/cm} = 20\hat{i} \text{ V/m}
\)
Step 4: Calculate the Torque
The torque \(\vec{\tau}\) acting on the dipole in an electric field is given by:
\(
\vec{\tau} = \vec{p} \times \vec{E}
\)
Substituting the values of \(\vec{p}\) and \(\vec{E}\):
\(
\vec{\tau} = (4 \times 10^{-6}\hat{i} - 4 \times 10^{-6}\hat{j} + 4 \times 10^{-6}\hat{k}) \times (20\hat{i})
\)
Using the properties of the cross product:
\(
\vec{\tau} = 4 \times 10^{-6} \times 20 (\hat{i} \times \hat{i}) - 4 \times 10^{-6} \times 20 (\hat{j} \times \hat{i}) + 4 \times 10^{-6} \times 20 (\hat{k} \times \hat{i})
\)
Since \(\hat{i} \times \hat{i} = 0\), we have:
\(
\vec{\tau} = 0 - 4 \times 10^{-6} \times 20 (-\hat{k}) + 4 \times 10^{-6} \times 20 \hat{j}
\)
\(
= 80 \times 10^{-6} \hat{k} + 80 \times 10^{-6} \hat{j} = 8 \times 10^{-5} \hat{j} + 8 \times 10^{-5} \hat{k}
\)
Step 5: Magnitude of the Torque
The magnitude of the torque vector is given by:
\(
|\vec{\tau}| = \sqrt{(8 \times 10^{-5})^2 + (8 \times 10^{-5})^2} = 8 \times 10^{-5} \sqrt{2}
\)
\(
= 8\sqrt{2} \times 10^{-5} \text{ Nm}
\)
Calculating the numerical value:
\(
|\vec{\tau}| \approx 1.13 \times 10^{-4} \text{ Nm}
\)
Final Answer
The torque acting on the dipole is approximately:
\(
\boxed{1.13 \times 10^{-4} \text{ Nm}}
\)
The position vectors of the charges are given as:
- Charge −4µC at point A (1, 0, 4):
\(
\vec{r_1} = 1\hat{i} + 0\hat{j} + 4\hat{k}
\)
- Charge +4µC at point B (2, -1, 5):
\(
\vec{r_2} = 2\hat{i} - 1\hat{j} + 5\hat{k}
\)
The dipole moment \(\vec{p}\) is given by the formula:
\(
\vec{p} = q \cdot \vec{d}
\)
where \(\vec{d}\) is the displacement vector from the negative charge to the positive charge.
\(
\vec{d} = \vec{r_2} - \vec{r_1} = (2\hat{i} - 1\hat{j} + 5\hat{k}) - (1\hat{i} + 0\hat{j} + 4\hat{k}) = (2-1)\hat{i} + (-1-0)\hat{j} + (5-4)\hat{k} = 1\hat{i} - 1\hat{j} + 1\hat{k}
\)
\(
\vec{p} = 4 \times 10^{-6} \cdot (1\hat{i} - 1\hat{j} + 1\hat{k}) = 4 \times 10^{-6}\hat{i} - 4 \times 10^{-6}\hat{j} + 4 \times 10^{-6}\hat{k}
\)
The electric field vector is given as:
\(
\vec{E} = 0.20\hat{i} \text{ V/cm} = 20\hat{i} \text{ V/m}
\)
The torque \(\vec{\tau}\) acting on the dipole in an electric field is given by:
\(
\vec{\tau} = \vec{p} \times \vec{E}
\)
\(
\vec{\tau} = (4 \times 10^{-6}\hat{i} - 4 \times 10^{-6}\hat{j} + 4 \times 10^{-6}\hat{k}) \times (20\hat{i})
\)
\(
\vec{\tau} = 4 \times 10^{-6} \times 20 (\hat{i} \times \hat{i}) - 4 \times 10^{-6} \times 20 (\hat{j} \times \hat{i}) + 4 \times 10^{-6} \times 20 (\hat{k} \times \hat{i})
\)
\(
\vec{\tau} = 0 - 4 \times 10^{-6} \times 20 (-\hat{k}) + 4 \times 10^{-6} \times 20 \hat{j}
\)
\(
= 80 \times 10^{-6} \hat{k} + 80 \times 10^{-6} \hat{j} = 8 \times 10^{-5} \hat{j} + 8 \times 10^{-5} \hat{k}
\)
The magnitude of the torque vector is given by:
\(
|\vec{\tau}| = \sqrt{(8 \times 10^{-5})^2 + (8 \times 10^{-5})^2} = 8 \times 10^{-5} \sqrt{2}
\)
\(
= 8\sqrt{2} \times 10^{-5} \text{ Nm}
\)
\(
|\vec{\tau}| \approx 1.13 \times 10^{-4} \text{ Nm}
\)
The torque acting on the dipole is approximately:
\(
\boxed{1.13 \times 10^{-4} \text{ Nm}}
\)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Knowledge Check
Two charges 4μCand−4μC are placed at (−3,0,0)and(3,0,0) cm respectively in an external field given by E=9×106r2Cm−2 , Find the energy of the system in this external field.
A−2.4JB2.4JC0D−1.4JElectric dipole of moment →p=pˆi is kept at a point (x, y) in an electric field →E=4xy2ˆi+4x2yˆj. Find the magnitude of force acting on the dipole.
A4py√y2+2x2B2py√y2+4x2C4py√y2+4x2D2py√y2+2x2A magnet of magnetic moment of 50 ˆiAm2 is placed along the x - axis in magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the manet is
A175ˆk Nm,B75ˆiNmC150ˆiNmD25√37ˆiNm,
Two charges of ±1000μC are separated by 2mm. This dipole so formed is held at an angle of 30∘ with a uniform electric field of 15×104N/C. Calculate the torque acting on the dipole.
View SolutionTwo charges one +5μC, and another −5μC ,are placed 1 mm apart . Calculate the dipole moment.
View SolutionTwo charges 2μCand−2μC are placed at points A and B 6 cm apart.
(a) Identify an equipotenital surface of the system.
(b) What is the direction of the electric field at every point on this surface ?
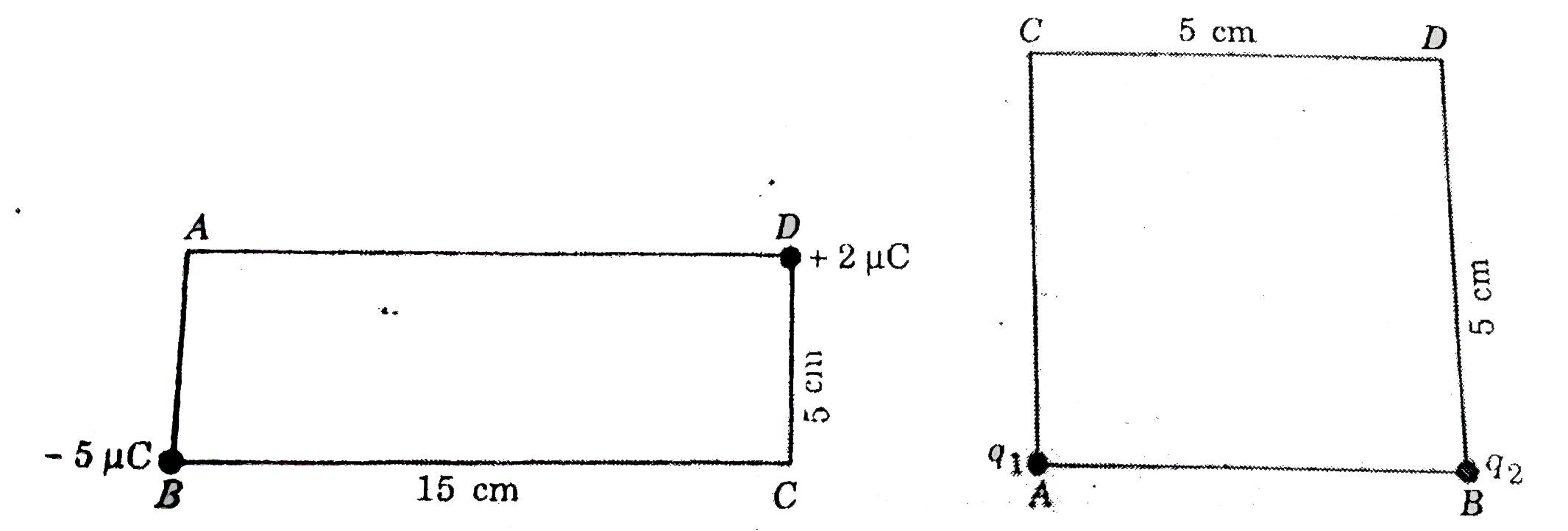
View SolutionThe sides of rectangle ABCD are 15 cm and 5 cm, as shown in figure. Point cahrges of −5μC and +2μC are placed at the vertices B and D respectively. Calculate electric potential at the vertices A and C. Also calculate the work done in carrying a charge of 3μC from A to C.
View SolutionA magnet of magnetic moment 50ˆiA−m2 is placed along the x-axis in a magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the magnet is
View Solution
