A long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cyclinder. What is the electric field in the space between the two cylinders ?
To find the electric field in the space between a long charged cylinder and a hollow coaxial conducting cylinder, we can follow these steps:
Step 1: Understand the Setup
We have a long charged cylinder with a linear charge density λ and a hollow conducting cylinder surrounding it. The charge on the inner cylinder creates an electric field in the space between the two cylinders.
Hint: Visualize the arrangement and identify the charge distribution.
Step 2: Identify the Charge on the Inner Cylinder
The linear charge density λ is defined as charge per unit length. Therefore, if we consider a length l of the charged cylinder, the total charge Q on the inner cylinder can be expressed as:
Q=λ⋅l
Hint: Remember that linear charge density relates to total charge over a specific length.
Step 3: Consider the Induced Charge on the Conducting Cylinder
Since the outer cylinder is a conductor, it will have an induced charge on its inner surface that is equal in magnitude but opposite in sign to the charge on the inner cylinder. Thus, the induced charge on the inner surface of the conducting cylinder is:
−Q=−λ⋅l
Hint: Conductors redistribute charge to maintain electrostatic equilibrium.
Step 4: Apply Gauss's Law
To find the electric field E at a distance r from the axis of the inner cylinder (where r is greater than the radius of the inner cylinder but less than the outer cylinder), we can use Gauss's Law:
ΦE=Qencϵ0
Here, ΦE is the electric flux through a Gaussian surface, and Qenc is the charge enclosed by the Gaussian surface.
Hint: Choose a cylindrical Gaussian surface coaxial with the charged cylinder.
Step 5: Calculate the Electric Flux
For a cylindrical Gaussian surface of radius r and length l:
ΦE=E⋅A=E⋅(2πrl)
where A is the surface area of the cylindrical Gaussian surface.
Hint: The electric field is uniform over the curved surface of the cylinder.
Step 6: Substitute the Enclosed Charge
The enclosed charge Qenc is simply the charge on the inner cylinder:
Qenc=λ⋅l
Substituting this into Gauss's Law gives:
E⋅(2πrl)=λlϵ0
Hint: Make sure to keep track of units and constants.
Step 7: Solve for the Electric Field
Now, we can solve for E:
E=λ2πϵ0r
Hint: This formula shows how the electric field varies with distance r from the charged cylinder.
Final Answer
The electric field in the space between the two cylinders is given by:
E=λ2πϵ0r
We have a long charged cylinder with a linear charge density λ and a hollow conducting cylinder surrounding it. The charge on the inner cylinder creates an electric field in the space between the two cylinders.
The linear charge density λ is defined as charge per unit length. Therefore, if we consider a length l of the charged cylinder, the total charge Q on the inner cylinder can be expressed as:
Q=λ⋅l
Since the outer cylinder is a conductor, it will have an induced charge on its inner surface that is equal in magnitude but opposite in sign to the charge on the inner cylinder. Thus, the induced charge on the inner surface of the conducting cylinder is:
−Q=−λ⋅l
To find the electric field E at a distance r from the axis of the inner cylinder (where r is greater than the radius of the inner cylinder but less than the outer cylinder), we can use Gauss's Law:
ΦE=Qencϵ0
Here, ΦE is the electric flux through a Gaussian surface, and Qenc is the charge enclosed by the Gaussian surface.
For a cylindrical Gaussian surface of radius r and length l:
ΦE=E⋅A=E⋅(2πrl)
where A is the surface area of the cylindrical Gaussian surface.
The enclosed charge Qenc is simply the charge on the inner cylinder:
Qenc=λ⋅l
Substituting this into Gauss's Law gives:
E⋅(2πrl)=λlϵ0
Now, we can solve for E:
E=λ2πϵ0r
The electric field in the space between the two cylinders is given by:
E=λ2πϵ0r
Similar Questions
A long charged cylinder of linear charge density λ surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders?
View SolutionA long charged cylinder of linear charged density à is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View Solution
Knowledge Check
Two parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
Aλ2πε0RN/CBzeroC2λπε0RN/CDλπε0RN/CA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformly charged line charge( linear charge density λ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
Aλ=RσBλ=−RσCλ=2πRσDλ=−2πRσAn infinite line charge of uniform electric charge density λ lies along the axis of an electrically conducting infinite cylindrical shell of radius R. At time t=0, the space inside the cylinder is filled with a material of permittivity ε and electrical conductivity σ. The electrical conduction in the material follows Ohm's law. Which one of the following graphs best describes the subsequent variation of the magnitude of current density j(t) at any point in the material ?
A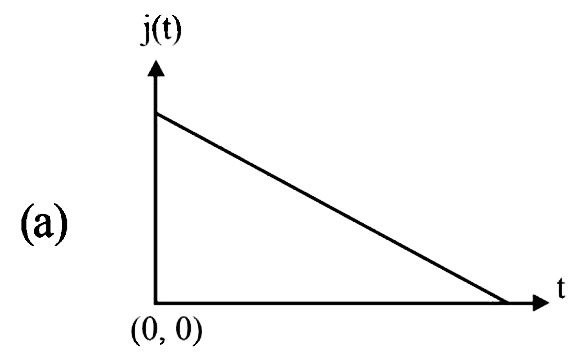 B
B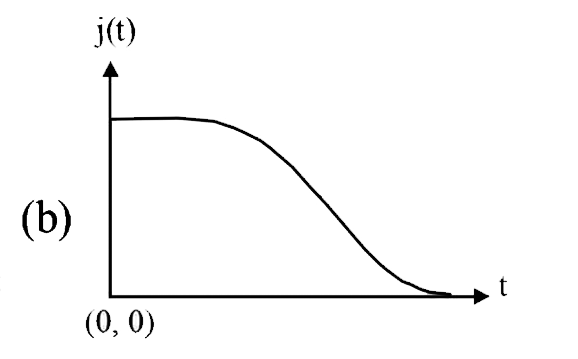 C
C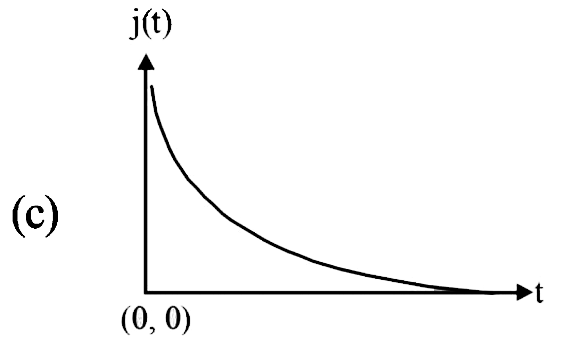 D
D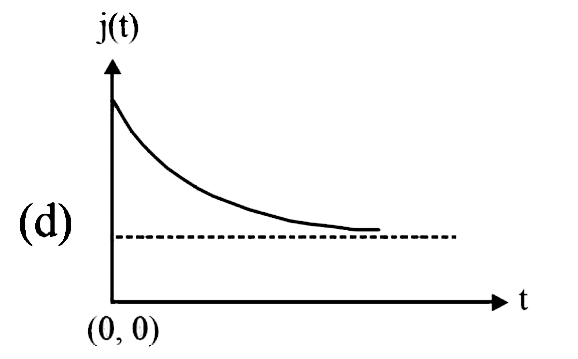
(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
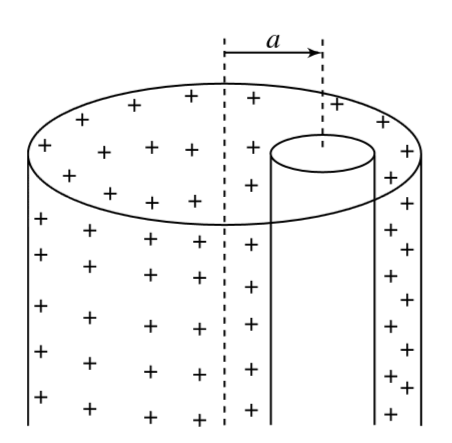
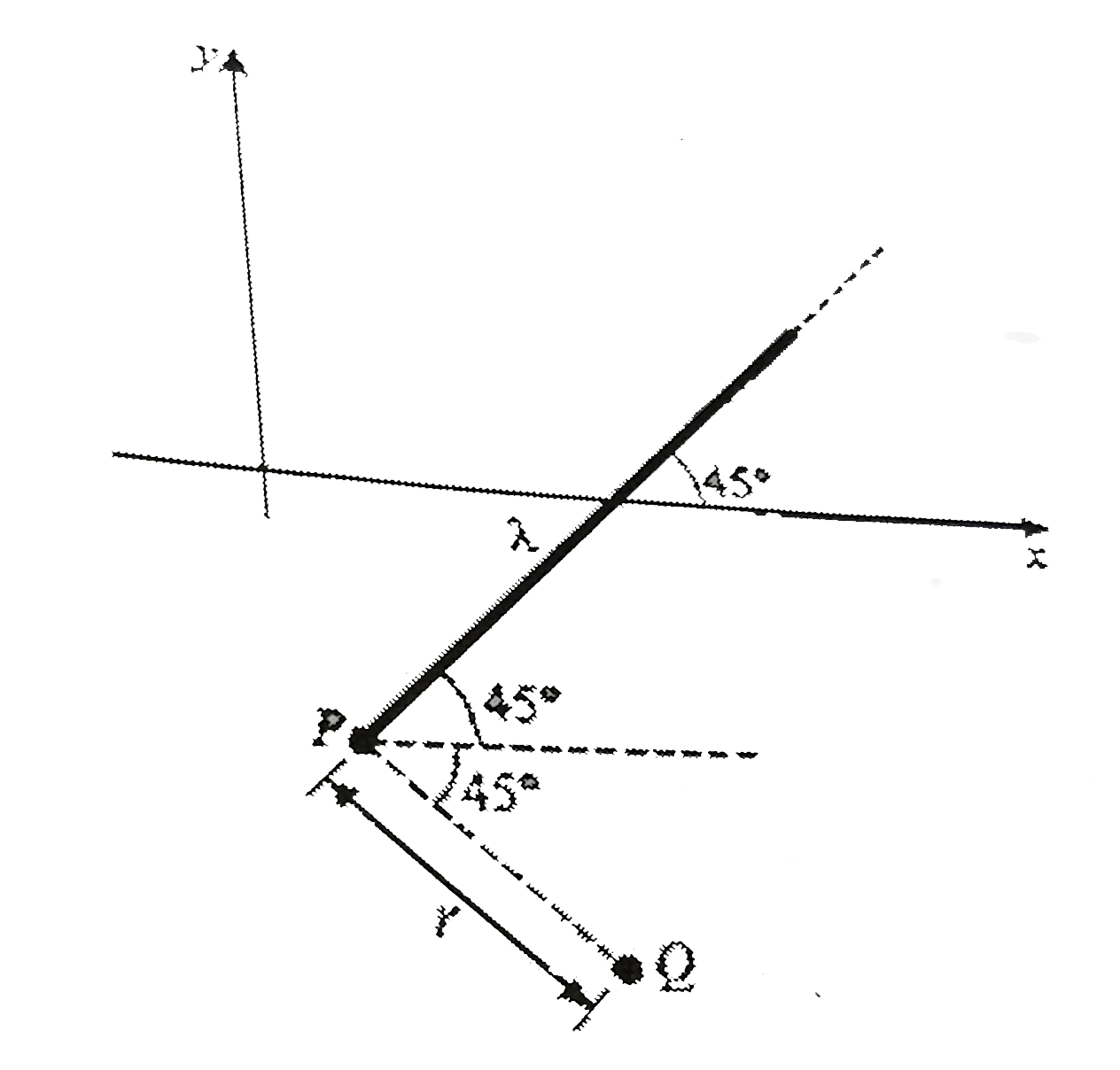
View SolutionA very long charged wire (lying in the xy plane ) which is having a linear charge density λ is having one of its end at a point P as shown in figure . What is electric field intensity at point Q :
View SolutionAn infinitely long time charge has linear charge density λC/m the line charge is along the line x=0,z=2m find the electric field at point (1,1,1) m.
View SolutionTwo parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
View SolutionConsider an infinite line charge having uniform linear charge density and passing through the axis of a cyclinder. What will be the effect on the flux passing through curved surface if the portions of the line charge outside the cyclinder is removed

View Solution

