Two infinitely large sheets having charge densities respectively are placed inbetween two plates such that there is no effect on charge distribution on plates. This charge is moved at an angle of with horizontal towards plate having charge density , through a distance a lt d. Find work done by electric force.
To solve the problem, we need to find the work done by the electric force when a charge q is moved at an angle of 45∘ towards a plate with charge density σ2. Let's break this down step by step.
Step 1: Understand the Electric Field
The electric field E between two infinite sheets with charge densities σ1 and σ2 is given by:
E=σ1−σ22ϵ0
where σ1>σ2 and ϵ0 is the permittivity of free space.
Step 2: Calculate the Electric Force
The electric force F acting on the charge q in the electric field is:
F=qE=q(σ1−σ22ϵ0)
Step 3: Determine the Displacement Components
The charge is moved at an angle of 45∘ towards the plate with charge density σ2 through a distance A. The horizontal component of this displacement is:
Δx=Acos(45∘)=A√2
Step 4: Calculate Work Done
The work done W by the electric force when the charge moves through the horizontal distance Δx is given by:
W=F⋅Δx
Substituting the expressions for F and Δx:
W=(qσ1−σ22ϵ0)(A√2)
Thus, the work done is:
W=qA(σ1−σ2)2√2ϵ0
Final Answer
The work done by the electric force when the charge q is moved towards the plate with charge density σ2 is:
W=qA(σ1−σ2)2√2ϵ0
---
The electric field E between two infinite sheets with charge densities σ1 and σ2 is given by:
E=σ1−σ22ϵ0
where σ1>σ2 and ϵ0 is the permittivity of free space.
The electric force F acting on the charge q in the electric field is:
F=qE=q(σ1−σ22ϵ0)
The charge is moved at an angle of 45∘ towards the plate with charge density σ2 through a distance A. The horizontal component of this displacement is:
Δx=Acos(45∘)=A√2
The work done W by the electric force when the charge moves through the horizontal distance Δx is given by:
W=F⋅Δx
Substituting the expressions for F and Δx:
W=(qσ1−σ22ϵ0)(A√2)
Thus, the work done is:
W=qA(σ1−σ2)2√2ϵ0
The work done by the electric force when the charge q is moved towards the plate with charge density σ2 is:
W=qA(σ1−σ2)2√2ϵ0
Similar Questions
Two uniformly charged large plane sheets S1 and S2 having charge densities σ1 and σ2 (σ1>σ2) are placed at a distance d parallel to each other. A charge q0 is moved along a line of length a(altd) at an angle 45∘ with the normal to S1. Calculate the work done by the electric field
View SolutionThree infinite long plane sheets carrying uniform charge densities σ1=−σ,σ2=+2σandσ3=3σ are placed parallel to the x-z plane at y=a,y=3aandy=4a as shown in the figure. What is the electric field at point 'P' ?
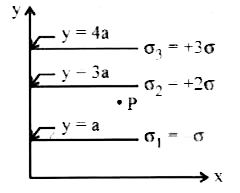
View Solution
Knowledge Check
Two infinitely long parallel sheets having surface charge densities +σand−σ respectively are separated by a small distance. The electric field in the region between the plates is
A0Bσ2∈0Cσ∈0D2σ∈0Two large parallel plane sheets have uniform charge densities + σand−σ. Determine the electric field (i) between the sheets, and (ii) outside the sheets.
Aσ2ε0Bσε0C2σε0DzeroTwo infinitely long. Parallel, thin sheets, having surface charge densities +σand−σ respectively are separated. By a small distance. The medium between the sheets is vacuum. The electric field in the region between the sheets is
AZeroBσ2∈0Cσ∈0D2σ∈0
Two thin infinite sheets have uniform surface densities of charge +σ and −σ . Electric field in the space between the two sheets is
View SolutionTwo plane sheets of charge densities +σand−σ are kept in air as shown in Fig. What are electric field intensities at points A and B ?

View SolutionTwo charged thin infinite plane sheets of uniform surface charge density σ+andσ− where |σ+|>|σ−| , intersect right angle Which of the following best represents the electric field lines for this system:
View SolutionTwo parallel plane sheet 1 and 2 carry uniform charge densities σ1 and σ2 as shown in fig.electric field in the region marked II is (σ1>σ2)

View SolutionThree non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
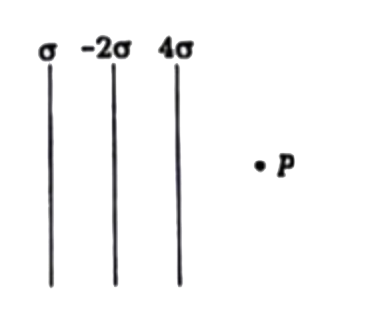
View Solution

