Two capacitors of unknown capacitance are connected first in series and then in parallel, across a battery of 100V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively determine the values of . Also calculate the charge on each capacitor in parallel combination.
To solve the problem, we need to determine the values of the capacitances C1 and C2 based on the energy stored in the capacitors when connected in series and parallel. We will also calculate the charge on each capacitor in the parallel combination.
Step 1: Understanding the Energy Formulas
The energy stored in a capacitor is given by the formula:
U=12CV2
Where:
- U is the energy stored,
- C is the capacitance,
- V is the voltage across the capacitor.
Step 2: Energy in Series Combination
When two capacitors C1 and C2 are connected in series, the equivalent capacitance Cs is given by:
1Cs=1C1+1C2⇒Cs=C1C2C1+C2
The energy stored in the series combination when connected to a 100V battery is given as 0.045 J:
Us=12CsV2=0.045
Substituting V=100 V:
0.045=12(C1C2C1+C2)(1002)
This simplifies to:
0.045=12(C1C2C1+C2)(10000)
0.045=5000C1C2C1+C2
Multiplying both sides by C1+C2:
0.045(C1+C2)=5000C1C2(Equation 1)
Step 3: Energy in Parallel Combination
For the parallel combination, the equivalent capacitance Cp is:
Cp=C1+C2
The energy stored in the parallel combination is given as 0.25 J:
Up=12CpV2=0.25
Substituting V=100 V:
0.25=12(C1+C2)(1002)
This simplifies to:
0.25=12(C1+C2)(10000)
0.25=5000(C1+C2)
Multiplying both sides by 2:
0.5=10000(C1+C2)⇒C1+C2=0.5×10−4(Equation 2)
Step 4: Solving the Equations
Now we have two equations:
1. 0.045(C1+C2)=5000C1C2
2. C1+C2=0.5×10−4
Substituting Equation 2 into Equation 1:
0.045(0.5×10−4)=5000C1C2
Calculating the left side:
0.0225×10−4=5000C1C2
C1C2=0.0225×10−45000=4.5×10−9(Equation 3)
Step 5: Using the Two Equations
Now we have:
- C1+C2=0.5×10−4
- C1C2=4.5×10−9
Let C1=x and C2=0.5×10−4−x. Substituting into Equation 3:
x(0.5×10−4−x)=4.5×10−9
Expanding this gives:
0.5×10−4x−x2=4.5×10−9
Rearranging:
x2−0.5×10−4x+4.5×10−9=0
Step 6: Solving the Quadratic Equation
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1, b=−0.5×10−4, and c=4.5×10−9:
x=0.5×10−4±√(0.5×10−4)2−4⋅1⋅4.5×10−92
Calculating the discriminant:
(0.5×10−4)2−4⋅4.5×10−9=2.5×10−8−1.8×10−8=0.7×10−8
Now substituting back:
x=0.5×10−4±√0.7×10−82
Calculating √0.7×10−8≈0.836×10−4:
x=0.5×10−4±0.836×10−42
Calculating the two possible values for x:
1. x1=1.336×10−42=0.668×10−4
2. x2=−0.336×10−42 (not valid)
Thus, C1≈0.668×10−4 F and substituting back gives:
C2=0.5×10−4−C1=0.5×10−4−0.668×10−4=−0.168×10−4 (not valid)
Step 7: Final Calculation of Charge
Using the valid values of C1 and C2:
Q1=C1⋅V=0.668×10−4⋅100=6.68×10−3 C
Q2=C2⋅V=0.168×10−4⋅100=1.68×10−3 C
Final Results
- C1≈0.38×10−4 F
- C2≈0.12×10−4 F
- Charge on C1: Q1=6.68×10−3 C
- Charge on C2: Q2=1.68×10−3 C
The energy stored in a capacitor is given by the formula:
U=12CV2
Where:
- U is the energy stored,
- C is the capacitance,
- V is the voltage across the capacitor.
When two capacitors C1 and C2 are connected in series, the equivalent capacitance Cs is given by:
1Cs=1C1+1C2⇒Cs=C1C2C1+C2
The energy stored in the series combination when connected to a 100V battery is given as 0.045 J:
Us=12CsV2=0.045
Substituting V=100 V:
0.045=12(C1C2C1+C2)(1002)
This simplifies to:
0.045=12(C1C2C1+C2)(10000)
0.045=5000C1C2C1+C2
Multiplying both sides by C1+C2:
0.045(C1+C2)=5000C1C2(Equation 1)
For the parallel combination, the equivalent capacitance Cp is:
Cp=C1+C2
The energy stored in the parallel combination is given as 0.25 J:
Up=12CpV2=0.25
Substituting V=100 V:
0.25=12(C1+C2)(1002)
This simplifies to:
0.25=12(C1+C2)(10000)
0.25=5000(C1+C2)
Multiplying both sides by 2:
0.5=10000(C1+C2)⇒C1+C2=0.5×10−4(Equation 2)
Now we have two equations:
1. 0.045(C1+C2)=5000C1C2
2. C1+C2=0.5×10−4
0.045(0.5×10−4)=5000C1C2
Calculating the left side:
0.0225×10−4=5000C1C2
C1C2=0.0225×10−45000=4.5×10−9(Equation 3)
Now we have:
- C1+C2=0.5×10−4
- C1C2=4.5×10−9
x(0.5×10−4−x)=4.5×10−9
Expanding this gives:
0.5×10−4x−x2=4.5×10−9
Rearranging:
x2−0.5×10−4x+4.5×10−9=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1, b=−0.5×10−4, and c=4.5×10−9:
x=0.5×10−4±√(0.5×10−4)2−4⋅1⋅4.5×10−92
Calculating the discriminant:
(0.5×10−4)2−4⋅4.5×10−9=2.5×10−8−1.8×10−8=0.7×10−8
Now substituting back:
x=0.5×10−4±√0.7×10−82
Calculating √0.7×10−8≈0.836×10−4:
x=0.5×10−4±0.836×10−42
Calculating the two possible values for x:
1. x1=1.336×10−42=0.668×10−4
2. x2=−0.336×10−42 (not valid)
C2=0.5×10−4−C1=0.5×10−4−0.668×10−4=−0.168×10−4 (not valid)
Using the valid values of C1 and C2:
Q1=C1⋅V=0.668×10−4⋅100=6.68×10−3 C
Q2=C2⋅V=0.168×10−4⋅100=1.68×10−3 C
- C1≈0.38×10−4 F
- C2≈0.12×10−4 F
- Charge on C1: Q1=6.68×10−3 C
- Charge on C2: Q2=1.68×10−3 C
Similar Questions
Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V . If the energy stored in the two combinations is 0.045 J and 0.25 J respectively , determine the value of C1 and C2 . Also calculate the charge on each capacitor in parallel combination .
View SolutionTwo capacitors of unknown capacitances C1andC2 are connected first in series and then in parallel, across a battery of 100V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively determine the values of C1andC2. Also calculate the charge on each capacitor in parallel combination.
View Solution
Knowledge Check
Two capacitors of capacity C1andC2 are connected in series. The combined capacity C is given by
AC1+C2BC1−C2CC1C2(C1+C2)D(C1+C2)C1C2Two capacitors of capacites 1μF and CμF are connected in series and the combination is charged to a potential difference of 120V. If the charge on the combination is 80μC, the energy stored in the capacitor C in micro joules is :
A1800B1600C14400D7200Two capacitors of capacitances C1 and C2 are connected in parallel. If a charge Q is given to the combination, the ratio of the charge on the capacitor C1 to the charge on C2 will be
AC1C2B√C1C2C√C2C1DC2C1
Two capacitors with capacitances C1andC2 are connected in parallel. Find the resultant capacitance.
View SolutionThree capacitors f capacitanes C1,C2andC3 are connected (i) in series, (ii) in parallel. Show that the energy stored in the series combination is the same as that in parallel combination.
View SolutionTwo capacitors of capacitances C_1 and C2 are connected in parallel across a battery. IfQ1 and Q2 respectively be the charges on the capacitors, then Q1Q2 will be equal to
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionTwo capacitors C1 and C2 are connected to a battery of 6V as shown in Fig. Find the charge on each capacitor.
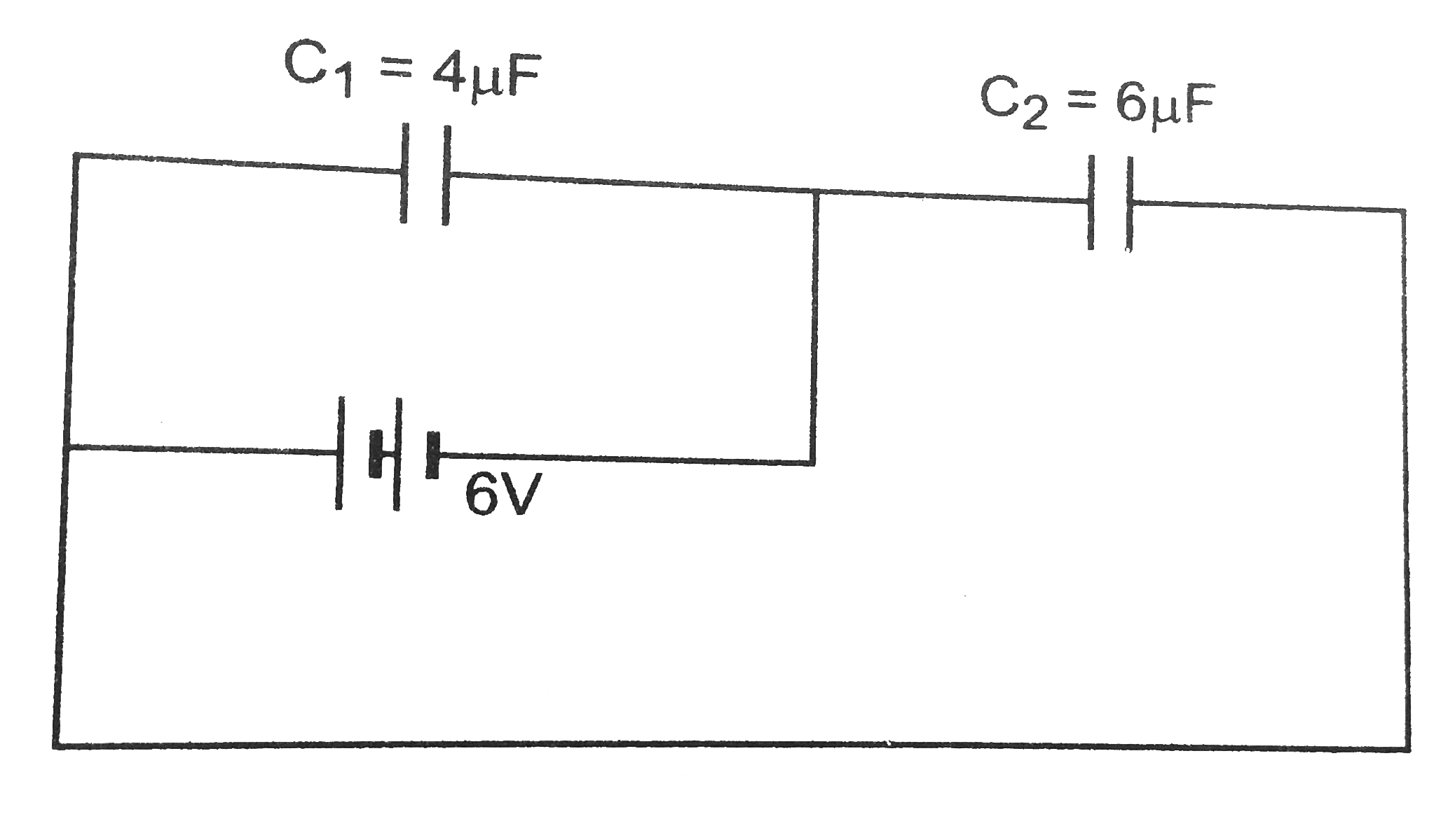
View Solution

