An infinite number of charges each numerically equal to q and of the same sign are placed along the x-axis at x=1,x=2,x=4,x=8 and so on. Find electric potential at x=0.
To find the electric potential at x=0 due to an infinite number of charges placed along the x-axis at positions x=1,2,4,8,…, we can follow these steps:
Step 1: Understand the Electric Potential Formula
The electric potential V due to a point charge q at a distance r is given by the formula:
V=14πϵ0qr
where ϵ0 is the permittivity of free space.
Step 2: Calculate the Distance of Each Charge from x=0
The distances of the charges from the point x=0 are:
- For the charge at x=1, r1=1
- For the charge at x=2, r2=2
- For the charge at x=4, r3=4
- For the charge at x=8, r4=8
- And so on...
Step 3: Write the Expression for Total Electric Potential
The total electric potential at x=0 due to all these charges can be calculated using the principle of superposition:
V=V1+V2+V3+V4+…
Substituting the values from the formula:
V=14πϵ0(q1+q2+q4+q8+…)
Step 4: Factor Out the Common Terms
We can factor out q4πϵ0:
V=q4πϵ0(1+12+14+18+…)
Step 5: Identify the Series as a Geometric Series
The series inside the parentheses is a geometric series where:
- The first term a=1
- The common ratio r=12
Step 6: Calculate the Sum of the Infinite Geometric Series
The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
Substituting the values:
S=11−12=112=2
Step 7: Substitute Back to Find the Electric Potential
Now substituting back into the expression for V:
V=q4πϵ0⋅2=2q4πϵ0
Final Answer
Thus, the electric potential at x=0 is:
V=q2πϵ0
The electric potential V due to a point charge q at a distance r is given by the formula:
V=14πϵ0qr
where ϵ0 is the permittivity of free space.
The distances of the charges from the point x=0 are:
- For the charge at x=1, r1=1
- For the charge at x=2, r2=2
- For the charge at x=4, r3=4
- For the charge at x=8, r4=8
- And so on...
The total electric potential at x=0 due to all these charges can be calculated using the principle of superposition:
V=V1+V2+V3+V4+…
Substituting the values from the formula:
V=14πϵ0(q1+q2+q4+q8+…)
We can factor out q4πϵ0:
V=q4πϵ0(1+12+14+18+…)
The series inside the parentheses is a geometric series where:
- The first term a=1
- The common ratio r=12
The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
Substituting the values:
S=11−12=112=2
Now substituting back into the expression for V:
V=q4πϵ0⋅2=2q4πϵ0
Thus, the electric potential at x=0 is:
V=q2πϵ0
Similar Questions
An infinite number of charges each equal to q, are placed along the X-axis at x=1,x=2,x=4,x=8,…….. and so on.
(i) find the electric field at a point x=0 due to this set up of charges.
(ii) What will be the elctric field if the above setup, the consecutive charges have opposite signs.
View SolutionAn infinite number of charges each equal to 4μC are placed along X-axis at x=1m,x=2m,x=4m,x=8m and so on. Find the total force on a charge of 1C plaaced at the origin.
View Solution
Knowledge Check
An infinite number of charges , each equal to q , are placed along the x - axis at x = 1, x=2,x=4,x=8 and so on . The potential at x = 0 due to this set of charges is
A4q2πε0B2q/4πε0Cq2πε0D2qπε0An infinite number of electric charges each equal to 5 nano-coulomb (magnitude) are placed along X-axis at x=1cm,x=2cm,x=8cm……and so on. In the setup if the consecutive charges have opposite sign, then the electrical field in Newton/Coulomb at x=0 is (14πε0=9×109N−m2/C2)
A12×104B24×104C36×104D48×104An infinite number of charges, each of magnitude q, are placed along x-axis at x = 1m, 2m, 4m, 8m, 16m and so on but the consecutive charges are of opposite sign starting with +q at x = 1m. A point charge q0 , kept at the origin, experiences a force of magnitude :
Aqq04πε0Bqq05πε0Cqq03πε0Dqq02πε0
An infinite number of charges each equal to q are placed along the x-axis at x=1m,x=2m,x=4m,x=8m, ... and so on. Find the potential and electric field at the point x = 0 due to this set of charges. What will be potential and electric field ifin the above set up if the consecutive charge have opposite sign?
[q2π∈0,q3π∈0,q6π∈0,q5π∈0]
View SolutionAn infinite number of charges, each equal to q, are placed along the x -axis at x=1,x=2,x=4,x=8, etc. The electric field at the point x=0 due to the set of charges is qnπɛ0. Find n.
View SolutionAn infinite number of charges, each equal to Q=10μC are placed along the x-axis at x=1,3,9…..m. Calculate the magnitude of electric field at x=0 if the consecutive charge have opposite signs.
View Solution[" An infinite number of "],[" charges each equal "],[" to 'q' are placed "],[" along the x-axis at "],[x=1,x=2,x=4,x=8......],[" The potential at the "],[" point "x=0" due to this "],[" set of charges is "]
View SolutionThree charges are placed along x-axis at x = - a x = 0 and x = a as shown in the figure. The potential energy of the system is
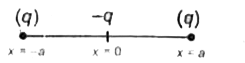
View Solution

