Two point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.
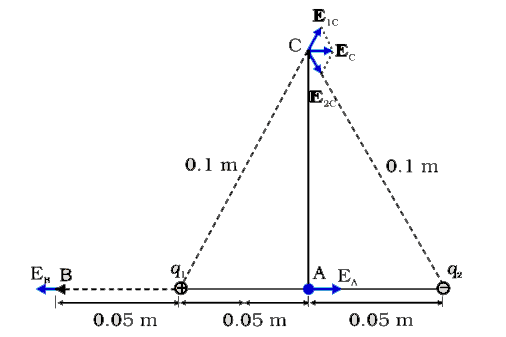
The charges +10−8Cand−10−8Cand−10−8C are held at P and Q respectively, PQ=0⋅1m
Also, PA=PB=0⋅05m
QA=0⋅05andCP=CQ=0⋅1m
At A, field intensity due to charge q1
=14π∈0q1×1AP2 , along PA
=9×109x10−8(0⋅05)2=36000N/C
Field intensity due to charge q2
=9×109x10−8(0⋅05)2 along AQ=36000N/C
∴ Net field intensity at A=36000+36000
=72000N/C=7⋅2×104N/C along AQ
At B. Field intensity due to charge q1
=14π∈0q1×1PB2 along PB producd
9×109×10−8(0⋅05)2=4000N/C
∴ Net field intensity at B=36000−4000
=32000N/c
3⋅2×104N/C , along PB produced
At C, Field intensity due to charge q1 ,
E1=14π∈0qPC2 , along PC.
E1=9×109×10−8(0−1)2=9×103N/C
Field intensity due to charge q2
E2=14π∈0q2QC2 along CQ,
E2=9×109×10−8(0⋅1)2=9×103N/C
Both, E1andE2 are equal in magnitude, acting at 60∘ to CR parallel to BA.
∴ Resulant intensity at R
=E1cos60∘+E2cos60∘=2E1cos60∘
=2×9×103×12=9×103N/C.
It is represented by CR parallel to BA. The components of −→E1 and −→E2 in directions ⊥ to CR cancel out.
Topper's Solved these Questions
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:CONCEPTUAL PROBLEMS
Explore 8 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:SHORT ANSWER QUESTIONS
Explore 9 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- ELECTRONIC DEVICESBook:PRADEEPChapter:ELECTRONIC DEVICESExercise:Fill in the Blanks
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
Two point charges q1andq2 of magnitude +10−8Cand−10−8C respectively are placed 0.1 m apart . Calculate the electric field at point B ,C and A
(##U_LIK_SP_PHY_XII_C01_E10_021_Q01.png" width="80%">
View SolutionTwo point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.

View Solution
Knowledge Check
Two point charges +10−7C and −10−7C are placed at A and B 20 cm apart as shown in the figure. Calculate the electric field at C, 20 cm apart from both A and B.
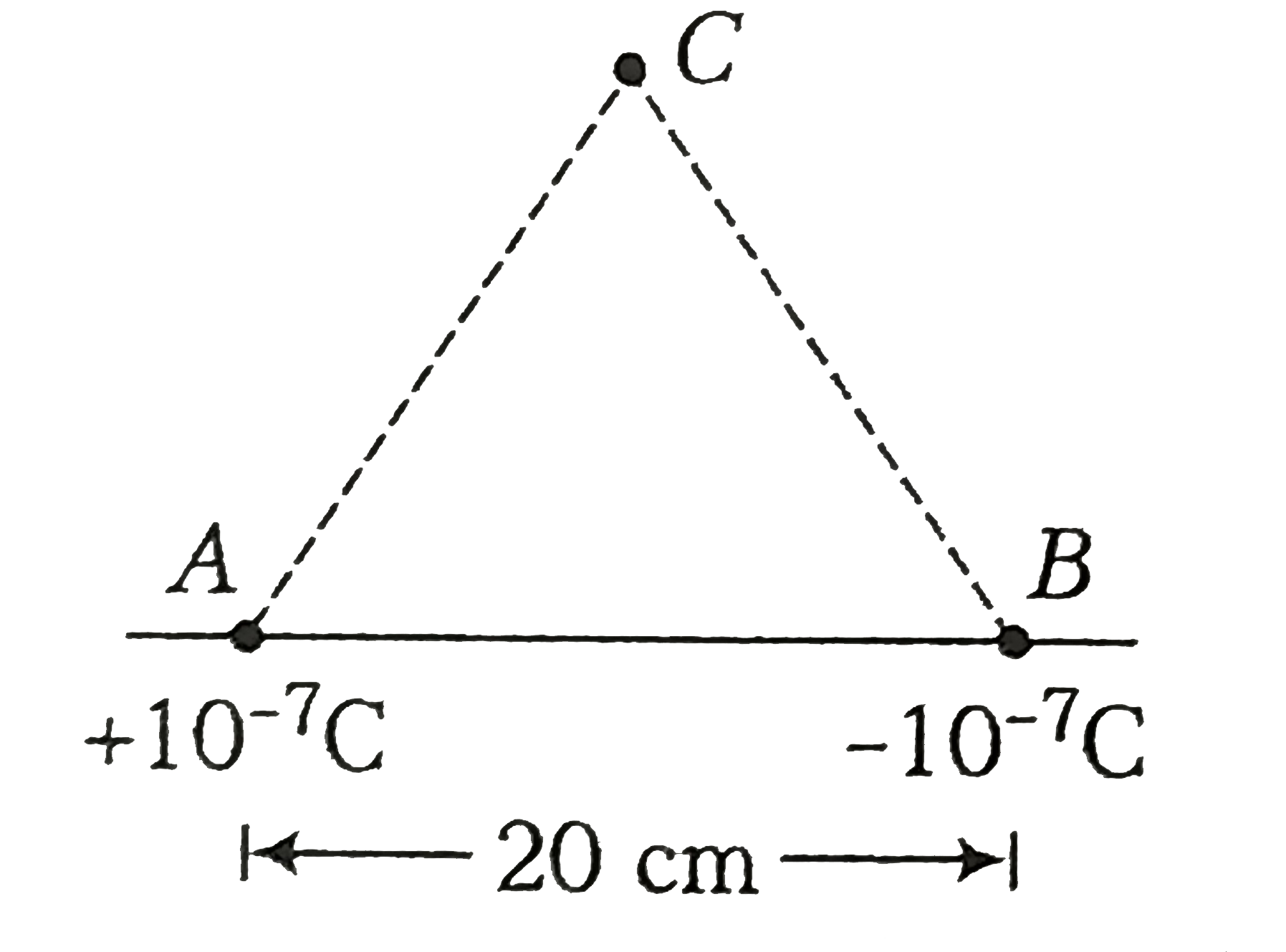 A1.5×10−5NC−1B2.2×104NC−1C3.5×106NC−1D3.0×105NC−1
A1.5×10−5NC−1B2.2×104NC−1C3.5×106NC−1D3.0×105NC−1In, the charges on C1,C2, and C3, are Q1,Q2, and Q3, respectively.
 .AQ2=8μCBQ3=12μCCQ1=20μCDQ2=12μC
.AQ2=8μCBQ3=12μCCQ1=20μCDQ2=12μC
Two pont chargees q1 and q2 of 2×10−8C and −2×10−8C respectively are placed 0.4 m apart. Calculate the electric field at the centre of the line joining the two charges.
View SolutionTwo point charges, q1=10×10−8Candq2=−2×10−8C, are separated by a distance of 60 cm in air.
Also calculate the electrostatic potential energy of the system.
View SolutionTwo particles A and B, having opposite charges2.0×10−6 and −2.0×10−6C , are placed at a separaton of 1.0 cm.(b) Calculate the electric field at a point on the axis of the dipole 1.0 m away from the centre. (c ) Calculate the electric field at a point on the perpendicular bisector of the dipole and 1.0 m away from the centre.
View SolutionFind the expression for the potential energy of a system of two point charges q1,andq2 glocated at →r1and→r2 respectively in an external electric field →E.
(b) Draw equipotential surfaces due to an isolated point charge (-q) and depict the electric field lines.
(c) Three point charges +1μC,−1μCand+2μC are initially infinite distance apart. Calculate the work done in assembling these charges at the vertices of an equilateral triangle of side 10 cm.
View SolutionTwo charges +0.2μμCand−0.2μμC are placed 10−6cm apart. Calculate electric field at an axial point at a distance of 10 cm from their middle point.
View SolutionTwo point charges of, 1 μC and -1 μC are kept at (-2 m, 0) and (2 m, 0) respectively. Calculate the electric field at point (0, 5 m).
View Solution

