A ray of light moving along the unit vector ( $- i - 2 j$ )undergoes refraction at an interface two media,which is the x-zplane. The refracive index for $y > 0$ ,it is $\sqrt{5} / 2$ .the unit vector along which the refracted ray moves is:

A

$(\frac{3 ˆ i - 5 ˆ j}{\sqrt{34}})$

B

$(\frac{- 4 ˆ i - 3 ˆ j}{5})$

C

$(\frac{- 3 ˆ i - 4 ˆ j}{5})$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

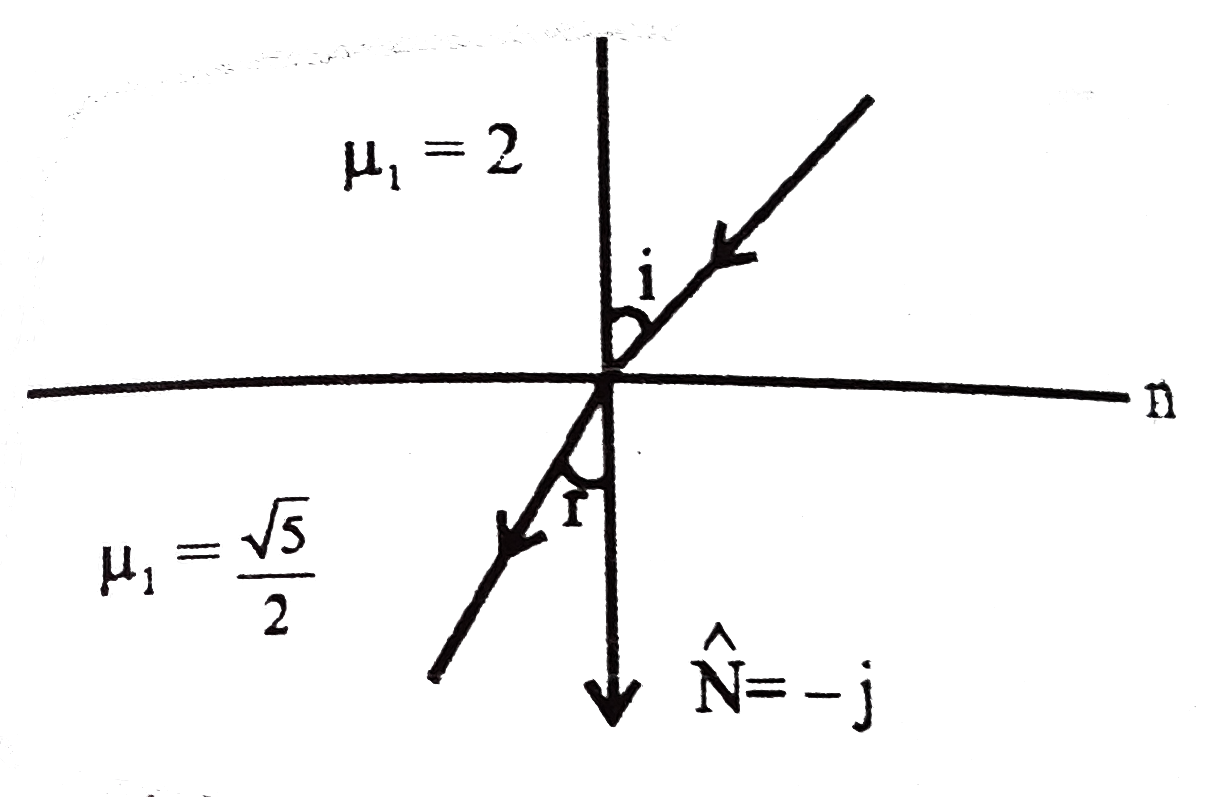
From snell's law
$μ_{1} [{ˆ r}_{i} \times ˆ N] = μ_{2} [{ˆ r}_{r} \times ˆ N] \Rightarrow 2 [\frac{- ˆ i - 2 ˆ j}{\sqrt{5}} \times (- ˆ j)] = \frac{\sqrt{5}}{2} ⎡ ⎢ ⎢ ⎣ \frac{(- ˆ i - y ˆ j)}{\sqrt{1 + y^{2}}} \times (- ˆ j) ⎤ ⎥ ⎥ ⎦$
$\frac{2}{\sqrt{5}} = (\frac{\sqrt{5}}{2}) (\frac{1}{\sqrt{1 + y^{2}}}) \Rightarrow \sqrt{1 + y^{2}} = \frac{5}{4} \Rightarrow y = \frac{3}{4}$
$ˆ r = \frac{(ˆ i - y ˆ j)}{\sqrt{1 + y^{2}}} \Rightarrow ˆ r = \frac{(- ˆ i - \frac{3}{4} ˆ j)}{\sqrt{1 + 9 / 16}}$
$ˆ r = \frac{- 4 ˆ i - 3 ˆ j}{5}$
Method II

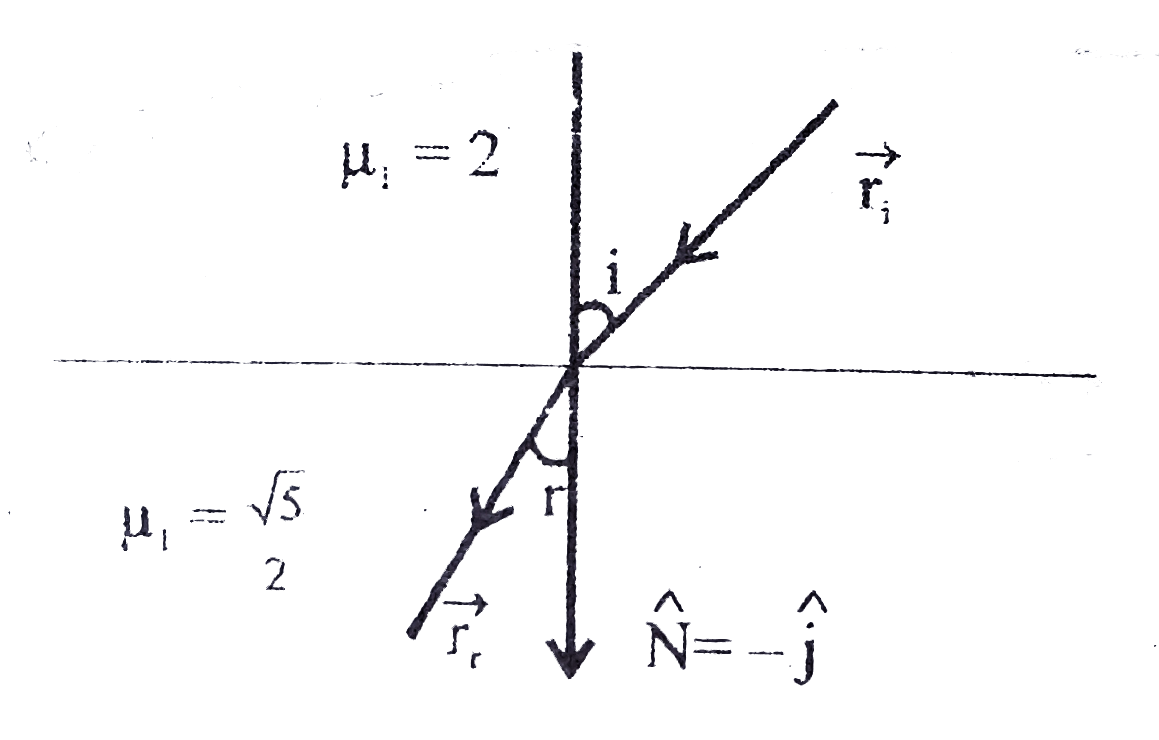
${\to r}_{i} . (- \to j) = r_{i} cos i$
$(- ˆ i - 2 ˆ j) . (- ˆ j) = \sqrt{5} cos i$
$cos i = \frac{2}{\sqrt{5}} or sin i = \frac{1}{\sqrt{5}}$
Applying Snell's law
$μ_{1} sin i = μ_{2} sin r$
$2 \times \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{2} sin r$
$sin r = \frac{4}{5}, cos r = \frac{3}{5}$
$\to r . (- ˆ j) = r_{r} cos r$
$(- ˆ i - y ˆ j) (- ˆ j) = \sqrt{1 + y^{2}} \frac{3}{5}$
$5 y = 3 \sqrt{1 + y^{2}} \Rightarrow y = \frac{3}{4}$
${ˆ r}_{r} = (\frac{- ˆ i - y ˆ j}{r_{B}}) \Rightarrow {ˆ r}_{r} = \frac{(- ˆ i - \frac{3}{4} ˆ j)}{\sqrt{1 + {(\frac{3}{4})}^{2}}}$
$ˆ r = \frac{- 4 ˆ i - 3 ˆ j}{5}$

Updated on:21/07/2023

|

Class 11 PHYSICS RAY OPTICS

Similar Questions

Knowledge Check

A ray of light moving along a vector $(3 \sqrt{2} ˆ i - 3 ˆ j - 3 ˆ k)$ undergoes refraction at an interface of two media which is y-z plane. The refractive index for $x \leq 0$ is 1 while for $x \geq 0$ it is $\sqrt{2}$ . Then,
ARefracted ray bend towards y-axis
BRefracted ray bend towards x-axis
CThe unit vector along the refracted ray is $\frac{\sqrt{3} ˆ i - ˆ j - ˆ k}{2}$
DThe unit vector along the refracted ray is $\frac{\sqrt{6} ˆ i - ˆ j - ˆ k}{\sqrt{8}}$
The unit vector along $\to A = 2 ˆ i + 3 ˆ j$ is :
A $2 ˆ i + 3 ˆ j$
B $\frac{2 ˆ i + 3 ˆ j}{2}$
C $\frac{2 ˆ i + 3 ˆ j}{3}$
D $\frac{2 ˆ i + 3 ˆ j}{\sqrt{13}}$
The unit vector along $\to A = 2 ˆ i + 3 ˆ j$ is $:$
A $2 ˆ i + 3 ˆ j$
B $\frac{2 ˆ i + 3 ˆ j}{2}$
C $\frac{2 ˆ i + 3 ˆ j}{3}$
D $\frac{2 ˆ i + 3 ˆ j}{\sqrt{3}}$

Recommended Questions

Home
Ask Doubt
Profile