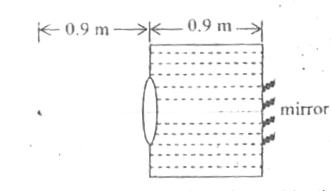
A thin equiconvex lens of glass of refractive index μ=3/2 & of focal length 0.3min air is sealed into an opeing at one end of a tank filled with water (μ=4/3) .Ont he oppostie side of the lens ,a mirror is placed inside the tank on the tank wall perpendicualar tot he lens axis ,as shown in figure .the seperation bertween the lens and the mirror is 0.8mA small object is placed outside the tank in front of the lens at a distance of 0.9m form the lens along its axis .Find the position (relative to the lens)of the image of the object fromed byt he stsyem.

The correct Answer is:90cmfrom the lens towards right
For radius of curvature
1f=(.aμg−1)(1R1−1R2)⇒1f=(.aμg−1)(1R−1−R)⇒130=(32−1)×2R
R=30cm
taking refraction from first curved surface
μ2v−μ1u=μ2−μ1R⇒32v−1−90=3/2−130⇒32v=160−190
32v=3−2180⇒v=270cm
this image will act as object for second surface.43v−32×270=4/3−3/2−(30)⇒v=120cm
this image will act a object for mirror ,u for mirror=(120−80)=40cm this image will formed by mirror infornt ata distance of 40cm.This image wil act as object for curved surface of lens.
u=−(80−40)cm⇒u=−40cm⇒32v−43×(−40)=3/2−4/330
32v+130=1180⇒1180−130⇒32v=1−6180⇒32v=−5180
32v=1−36⇒v=−54cm
This image will act as object for second refraction.
1v−32(−54)=1−3/2−30⇒1v+136=160⇒1v=160−136
1v=3−5180⇒v=180−2
v=−90cm
So image wil formed at 90cmtowards right of lens.
Similar Questions
A thin equiconvex lens made of glass of refractive index 3/2 and of focal length 0.3m in air is sealed into an opening at one end of a tank filled with water (μ=32). On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis as shown in Figure. The separation between the lens and mirror is 0.8m. A small object is placed outside the tank in front of the lens at a distance oa 0.9m from the lens along its axis. Find the position (relative to lens) of the image of the object formed by the system.

View SolutionA thin equiconvex lens of glass of refractive side of 3/2 and of focal length 0.3 m is sealed into an opening at end of a tank filled with water (p=4/3). on the opposite side of the lens a mirror is placed inside the tank with the tank wall perpendicular to the sense axis as shown in figure
The separation between the lens and mirror is 0.8 m. A small object is placed outside the tank is front of the lens, at a distance of 0.9 m from the lens along its axis. Find the position (relative to the lens) of the image of the object formed by the system.
View Solution
Knowledge Check
A thin lens made of glass of refractive index μu=1.5 has a focal length equal to 12 cm in air. It is now immersed in water (μ=43). Its new focal length is
A48 cmB36 cmC24 cmD12 cmAn equiconvex lens of glass (μg=1.5) of focal length 10 cm is silvered on one side. It will behave like a
Aconcave mirror of focal length 10 cmBconvex mirror of focal length 5.0 cmCconcave mirror of focal length 2.5 cmDconvex mirror of focal length 20cmA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. The radius of curvature of the convex surface isA10cmB15cmC20cmD25cm
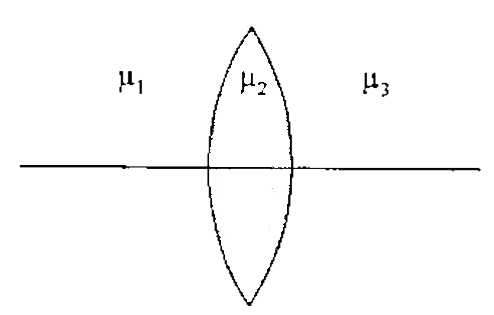
An equiconvex lens of refractive index μ2 is placed such that the refractive :
View SolutionA convex lens made of a glass of refractive index 3/2 has a focal length 'f' in air. If it is immersed into water of refractive index 4/3, then with calculation, predict the new focal length of the lens inside water.
View SolutionA glass convex lens of refractive index 32 has got a focal length equal to 0.3 m. Find the focal length of the lens if it is immersed in water of refractive index4/3.
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionAn equiconvex lens of refractive index n2 is placed such that the refractive index of the surrouding media is as shown. The lens :
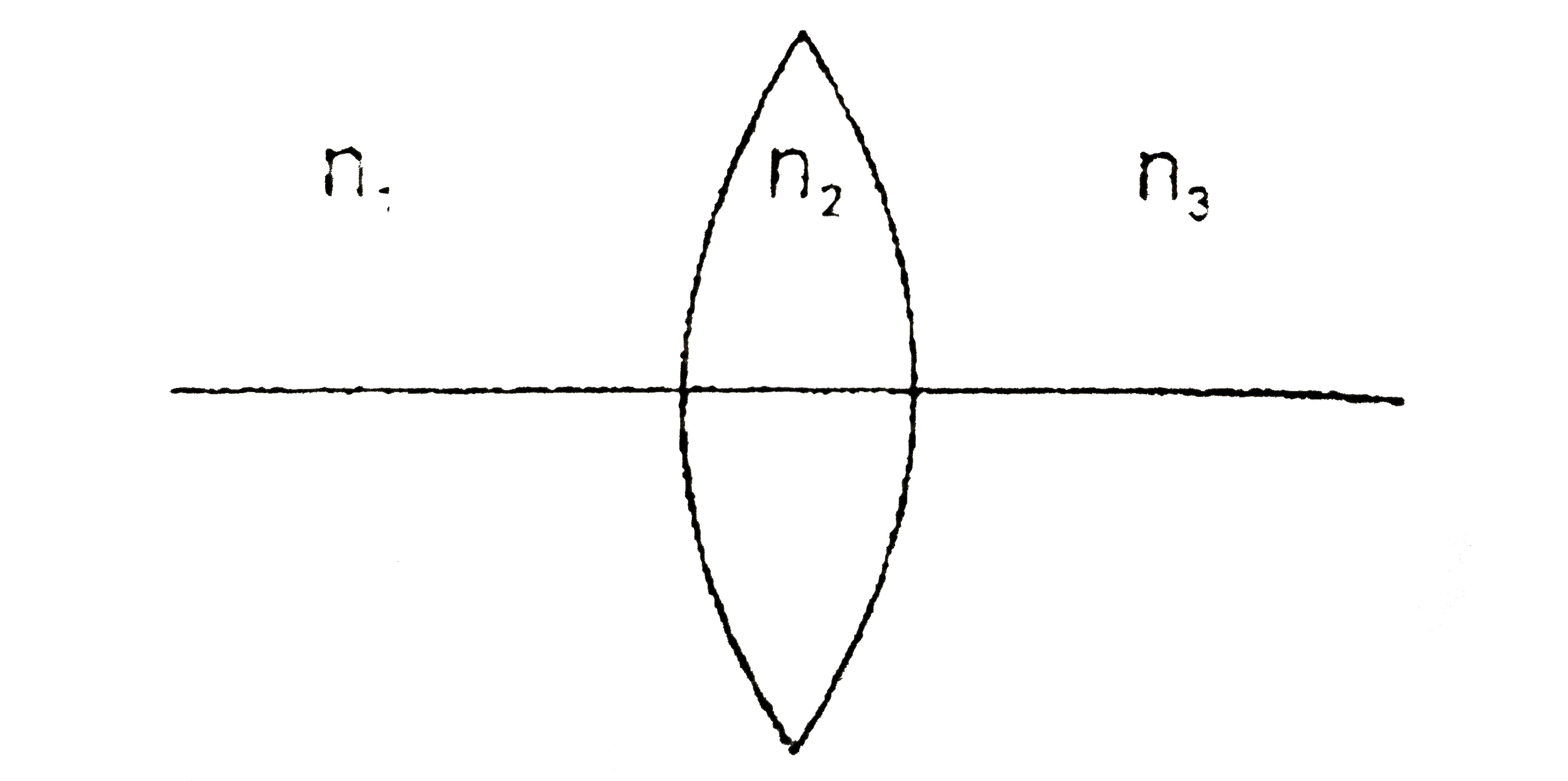
View Solution
