An equilateral prism deviates a ray through $23^{\circ}$ for two angles of incidence differing by $23^{\circ}$ find $μ$ of the prism?

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{\sqrt{43}}{5}$

$δ = (i_{1} + i_{2}) - A$
$23^{\circ} = (i_{1} + i_{2}) - 60^{\circ}$
$i_{1} + i_{2} = 83^{\circ}$
Given that $i_{2} - i_{1} = 23^{\circ} \dots \dots \dots . (i)$
$i_{2} = 53^{\circ}, i_{1} = 30^{\circ} \dots \dots \dots . . (i i)$
taking refraction at $A B$
$1 {sin i}_{1} = μ {sin r}_{1}$
$1 {sin 30}^{\circ} = μ {sin r}_{1}$
$\frac{1}{2} = μ {sin r}_{1} ... ... ... (i i i)$
Taking refraction at $A C$
$1 {sin i}_{2} = μ {sin r}_{2} \Rightarrow 1 {sin 53}^{\circ} = μ {sin r}_{2} \Rightarrow \frac{4}{5} = μ {sin r}_{\circ}$
$\frac{4}{5} = μ sin (A - r_{1})$ since $r_{1} + r_{1} = A$
$\frac{4}{5} = μ sin (60^{\circ} - r_{1}) ... . . (i v)$
from eq.(i)&(iii)
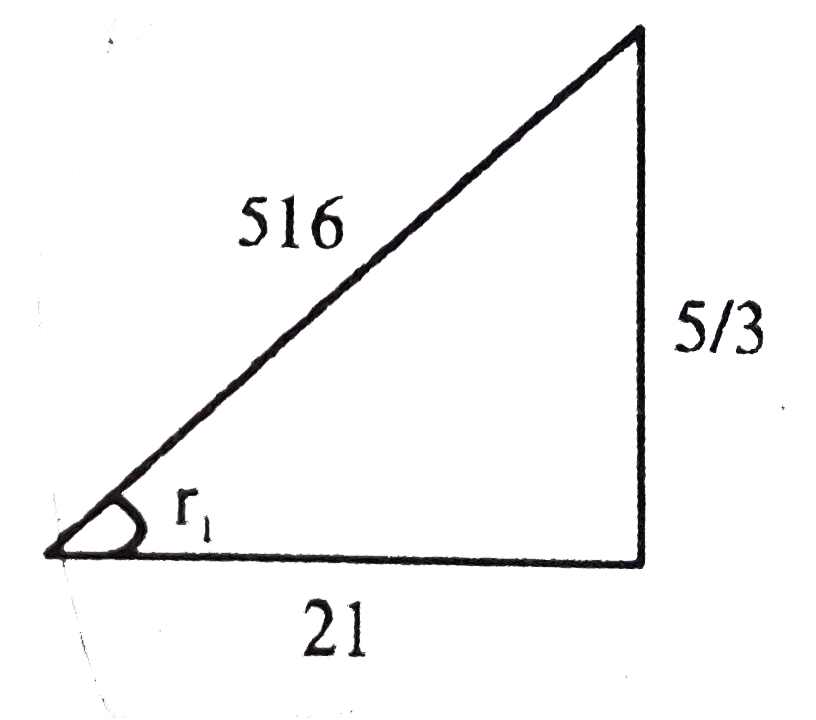
$\frac{5}{8} = \frac{{sin r}_{1}}{sin (60^{\circ} - r_{1})} \Rightarrow 5 sin (60^{\circ} - r_{1}) = 8 {sin r}_{1}$
$5 [{sin 60}^{\circ} {cos r}_{1} - {cos 60}^{\circ} {sin r}_{1}) = 8 {sin r}_{1} \Rightarrow 5 [\frac{\sqrt{3}}{2} {cos r}_{1} - \frac{1}{2} {sin r}_{1}] = 8 {sin r}_{1}$
$= 5 \sqrt{3} {cos r}_{1} - 5 {sin r}_{1} = 16 {sin r}_{1} \Rightarrow 21 {sin r}_{1} = 5 \sqrt{3} {cos r}_{1}$
${tan r}_{1} = \frac{5 \sqrt{3}}{21}$ or ${sin r}_{1} = \frac{5 \sqrt{3}}{\sqrt{516}}$
from eq.(i) $\frac{1}{2} = μ {sin r}_{1} \Rightarrow \frac{1}{2} = μ \times 5 \sqrt{\frac{3}{516}}$
$\frac{1}{2} = μ \times 5 \sqrt{\frac{1}{172}} \Rightarrow = \frac{\sqrt{172}}{5 \times 2} \Rightarrow μ = \frac{\sqrt{43}}{5}$

Updated on:21/07/2023

|

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Similar Questions

Knowledge Check

An equilateral prism deviates a ray through $45^{\circ}$ for the two angles of incidence differing by $20^{\circ}$ . The angle of incidence is
A ${62.5}^{\circ}$
B ${42.5}^{\circ}$
CBoth are correct
DBoth are wrong
An equilateral prism deviates a ray through $40^{\circ}$ for two angles of incidence differing by $20^{\circ}$ . The possible angles of incidences is
A $30^{\circ}$
B $50^{\circ}$
C $20^{\circ}$
D $60^{\circ}$
An equilateral deviates a ray through $45^{\circ}$ for the two angle of incidence differing by $20^{\circ}$ . The angle of incidence is
A $60^{\circ}$
B $40^{\circ}$
C $120^{\circ}$
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile