A beam of parallel rays of width b propagates in glass at an angle $θ$ to its plane face .The beam width after it goes over to air through this faceis…….if the refractive index of glass is $μ . v$
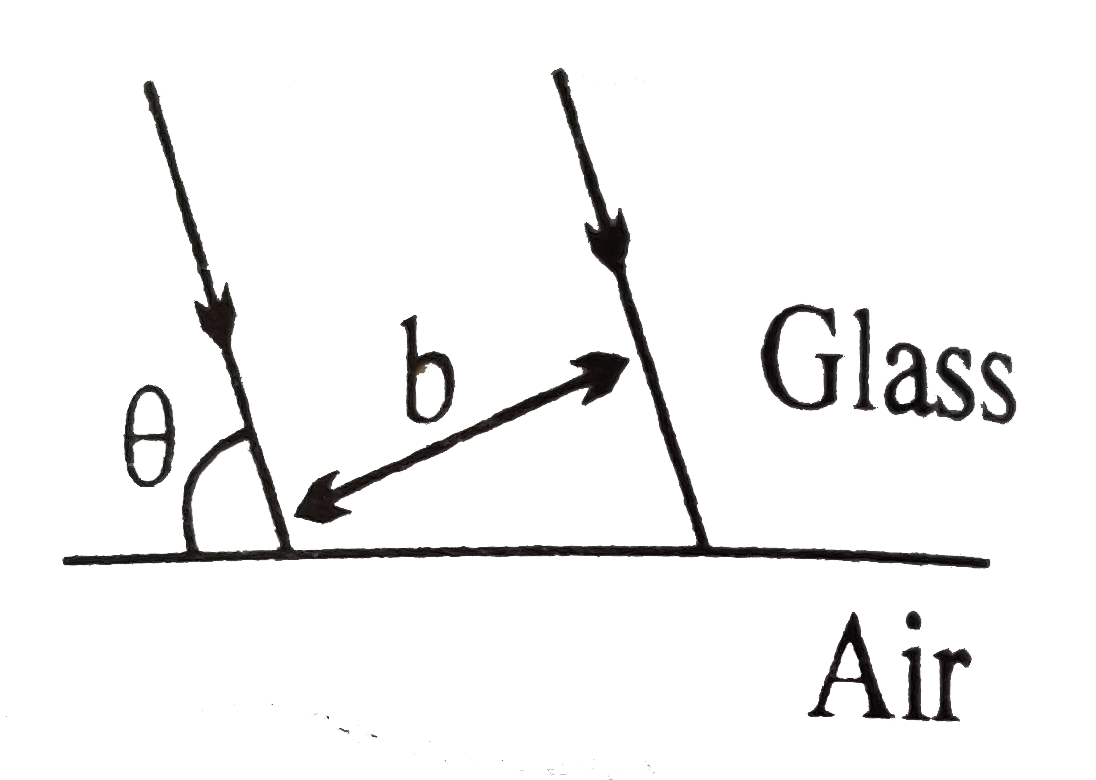
$A beam of parallel rays of width b propagates in glass at an anglethetato its plane face .The beam width after it goes over to air through this faceis…….if the refractive index of glass is mu.v$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{b {(1 - μ^{2} o s^{2} θ)}^{1 / 2}}{sin θ}$

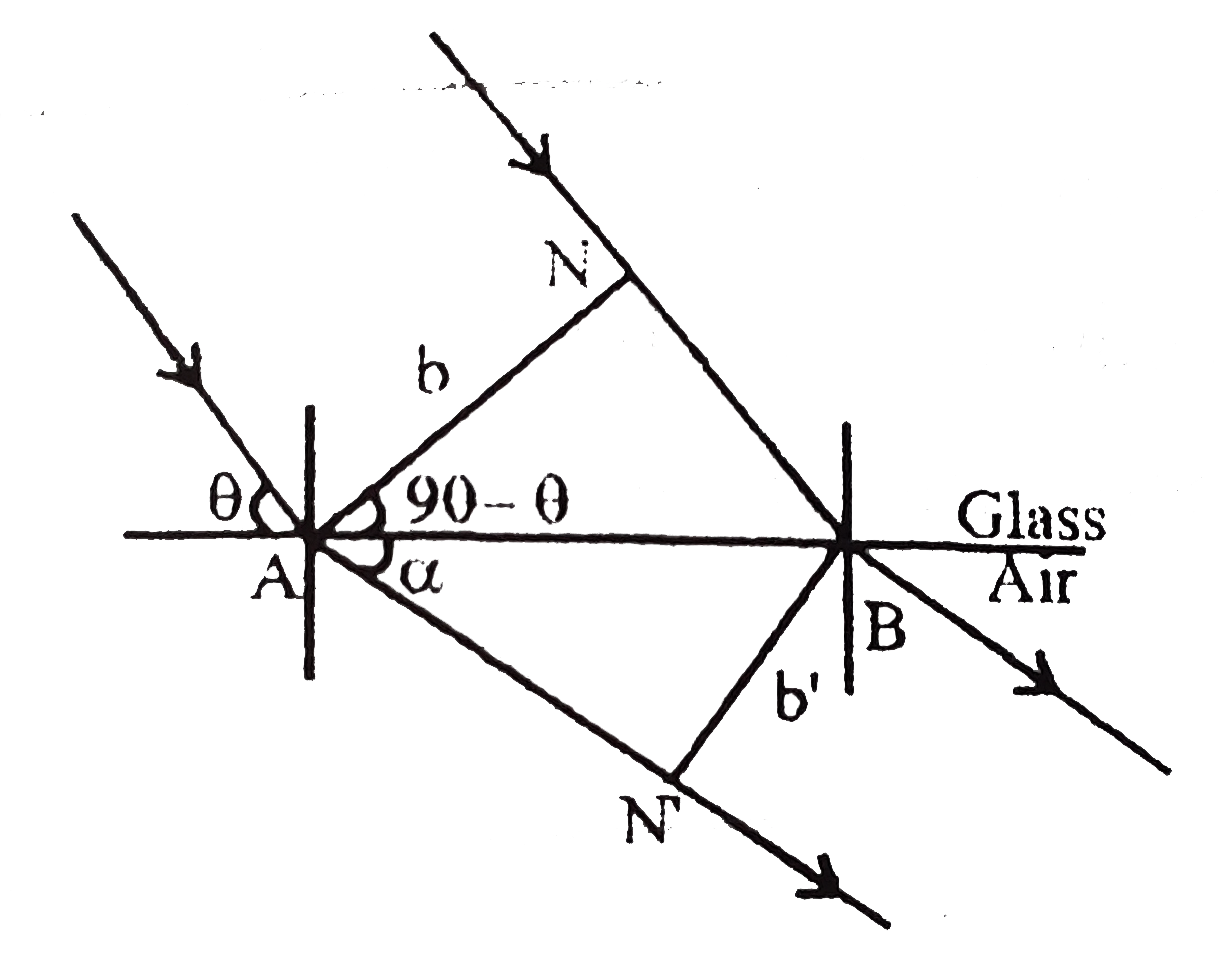
From snell's law
$μ sin (90^{\circ} - θ) = 1 sin (90^{\circ} - α)$
$μ cos θ = 1 - cos α$
$cos α = μ cos θ \dots \dots . (1)$
From right angle triangle $A B N$
$\frac{b}{A B} = cos (90 - θ)$
$A B = \frac{b}{sin θ} ... . . (2)$
From right angle triangle $A B N'$
$\frac{b'}{A B} = sin α$
$b' = A B sin α ... . (3)$
from (2)and(3)
$b' = \frac{b}{sin θ} \sqrt{1 - {cos}^{2} α} ... ... ... . . (4)$
from(1)&(4)
$b' \frac{b}{sin θ} \sqrt{1 - μ^{2} {cos θ}^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Similar Questions

Knowledge Check

Question 1 - Select One
A paralel beam of monochromatic light is incident on a glass slab at an angle of incidentce $45^{\circ}$ . Find the ratio of width of beam in glass to that in air ( If refractive index of glass is 1.5).
A $\frac{1}{1.2475}$
B $\frac{1}{1.4134}$
C $\frac{1}{1.732}$
D $1$
Question 2 - Select One
The angles of incidence and refraction of a monochromatic ray of light of wavelength $λ$ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread $δ λ$ in wavelength about a mean wavelength $λ$ is refracted at the same air-glass interface. The refractive index $μ$ of glass depends on the wavelength $λ$ as $μ (λ) = a + b / λ 2$ where a and b are constants. Then the angular spread in the angle of refraction of the beam is
A $∣ ∣ ∣ \frac{sin i}{λ^{3} cos r} δ λ ∣ ∣ ∣$
B $∣ ∣ ∣ \frac{2 b}{λ^{3}} δ λ ∣ ∣ ∣$
C $∣ ∣ ∣ \frac{2 b tan r}{a λ^{3} + b λ} δ λ ∣ ∣ ∣$
D $∣ ∣ ∣ ∣ \frac{2 b (a + b / λ^{2}) sin i}{λ^{3}} δ λ ∣ ∣ ∣ ∣$
Question 3 - Select One
A ray of light is travelling from glass to air. The angle of incidence in glass is $35^{\circ}$ , and angle of refraction in air $60^{\circ}$ . What is the refractive index of glass w.r.t. air ? $[{sin 35}^{\circ} = (0.5736)]$
A $1.9$
B $0.5$
C $1.51$
D $2.0$

Recommended Questions

Home
Ask Doubt
Profile