Focal length of two lens arefandf′ans dispersive powers are ω0and2ω0.To form achromatic combination from these-
(1)f′=2f,(2)f′=−2f (3)f′=−f/2
For achromatic combination
ωω'=−ωω'
ωω'=ω02ω0=12
−ff'=12 or f'=-2f
Similar Questions
Knowledge Check
Focal lengths of two lenses are f and f' and dispersive powers of their materials are ω and ω'. To form achromatic combination from these, which relation is correct ?
Af' = 2fBf' = -2fCf' = f/2Df' = -f/2Focal lengths of two lenses are f and f and dispersive powers of their materials are ω and omega^(')'. To form achromatic combination from these, which relation is correct?
Aω=ω0,2ω0,f′=2fBω=ω0,2ω0,f′=−2fCω=ω0,2ω0,f′=f2Dω=ω0,2ω0,f′=−f2Focal lengths of two lenses are f and f' and dispersive powers of their materials are ω and ω'. To form achromatic combination from these, which relation is correct ?
Aω=ω0, ω'=2ω0, f'=2fBω=ω0, ω'=2ω0, f'=f/2Cω=ω0, ω'=2ω0, f'=−2fDω=ω0, ω'=2ω0, f'=−f/2
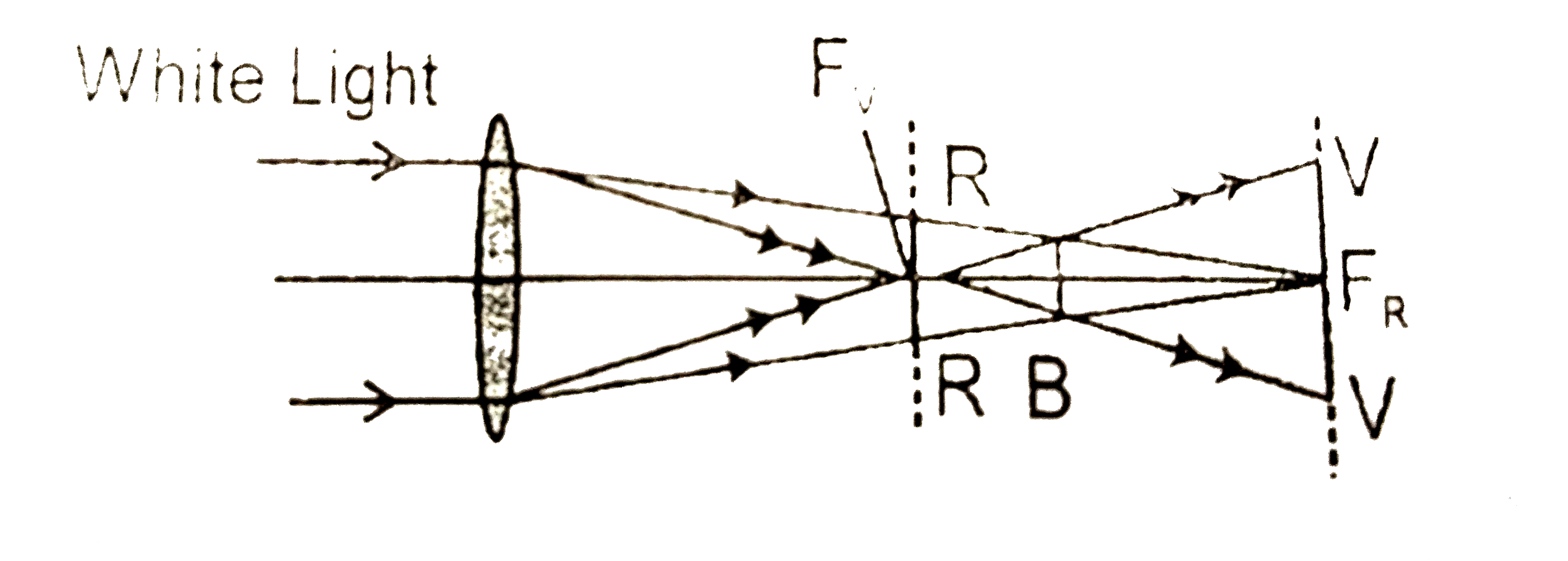
The image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
The dispersive power of crown and fint glasses are 0.02 and 0.04 respectively. An achromtic converging lens of focal length 40cm is made by keeping two lenses, one of crown glass and the other of flint glass, in contact with each other. The focal lengths of the two lenses are :
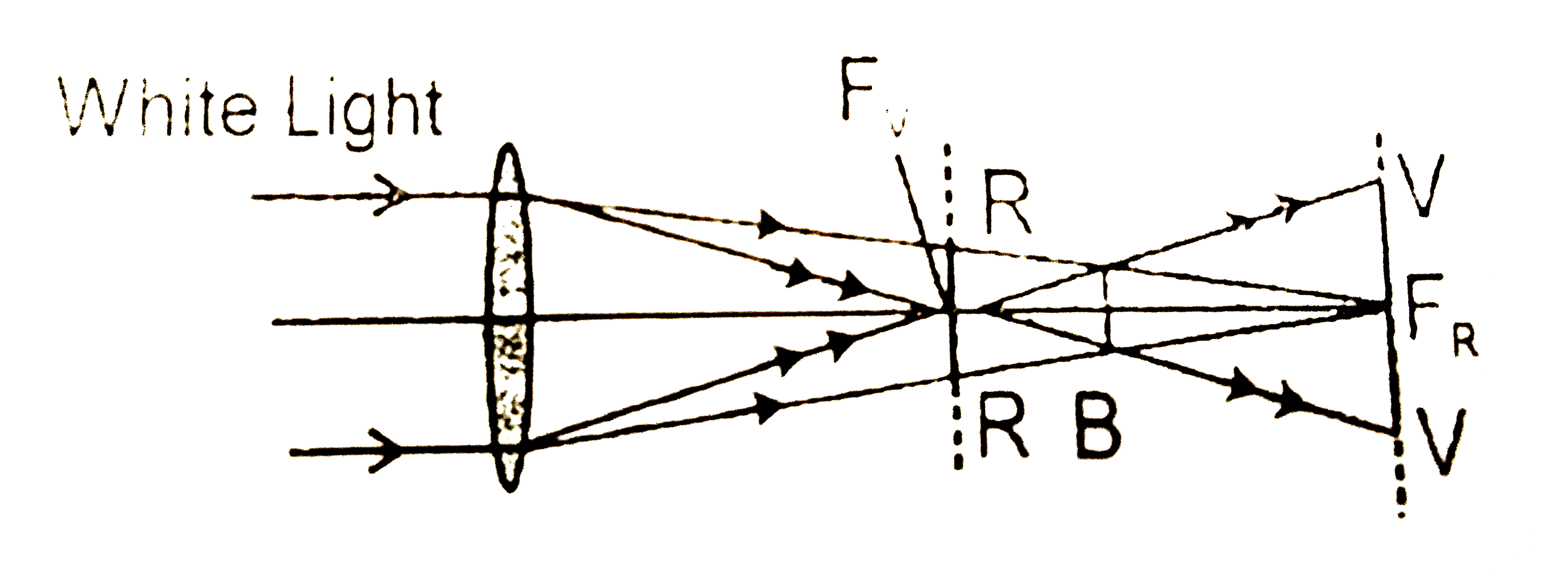
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
A combination is made of two lenses of focal lengths f and f' in contact , the dispersive powers of the materials of the lenses are ω and ω' . The combination is achromatic when :
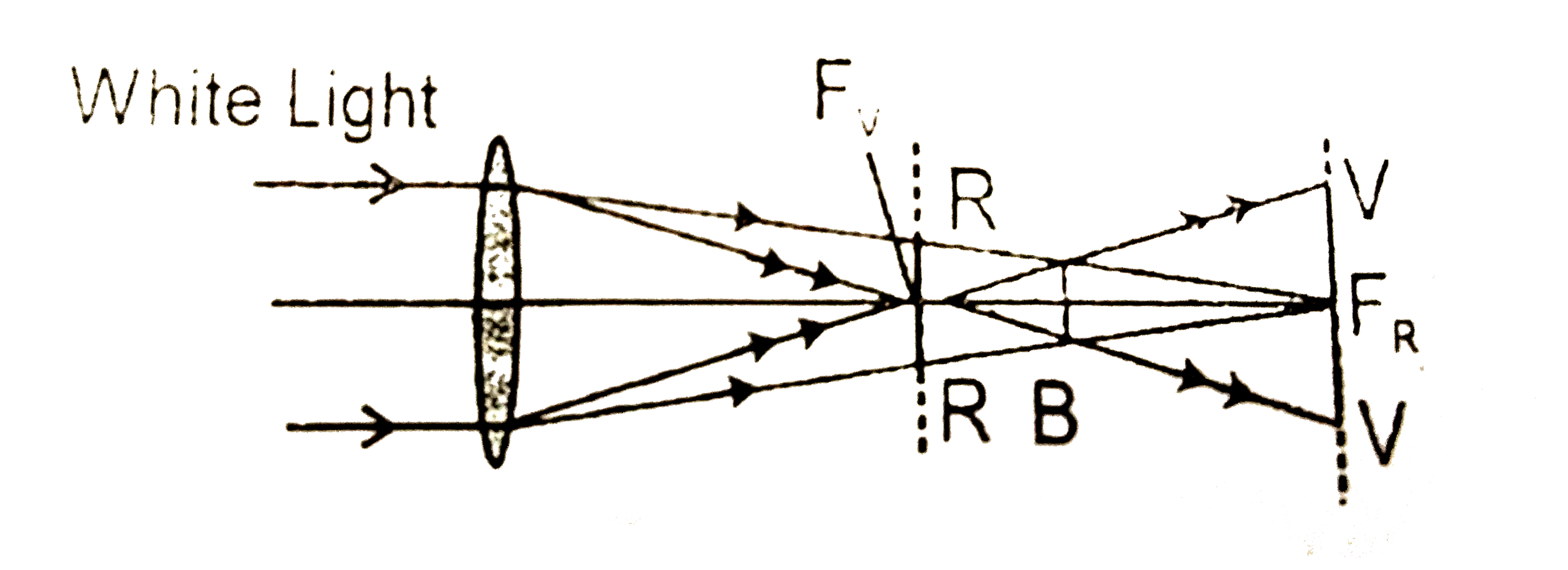
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
Chromatic aberration in a spherical concave mirror is proportional to :
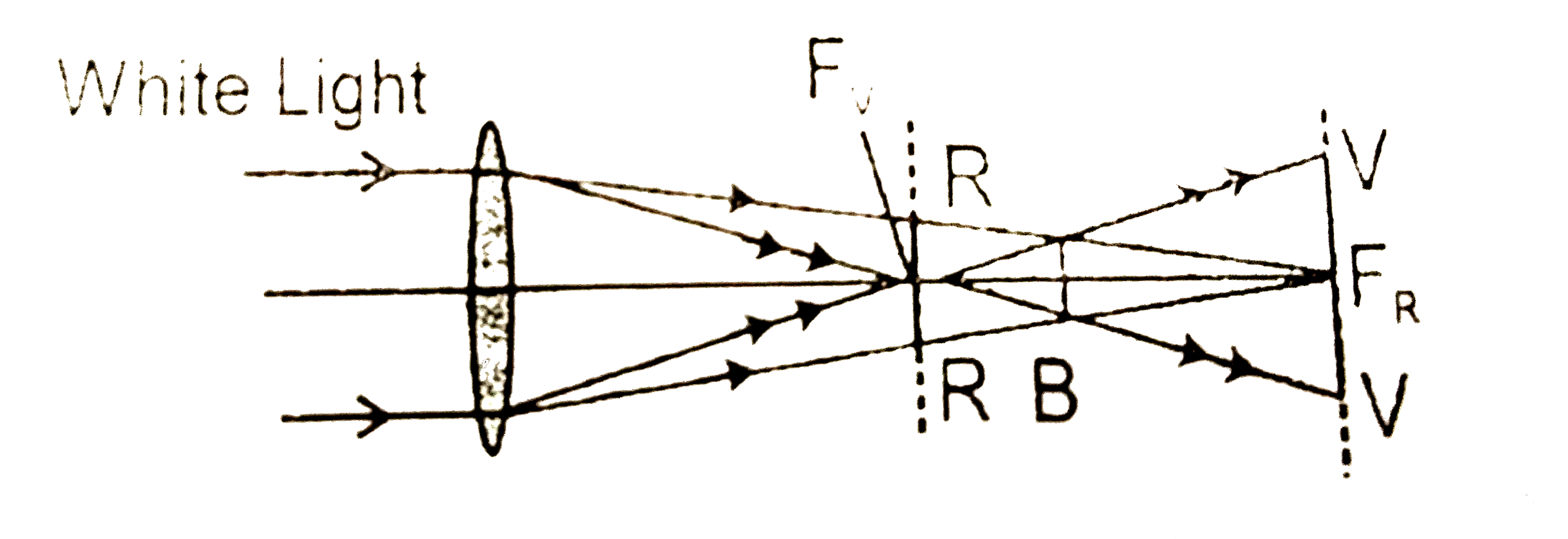
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
Chromatic aberration in the formation of image by a lens arises because :
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)

Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
Chromatic aberration of a lens can be corrected by :
View Solution
