A body is lauched from the earth's surface a an angle α=30∘ to the horizontal at a speed v0=√1.5GMR. Neglecting air resistance and earth's rotation, find (a) the height to which the body will rise. (ii) the radius of curvature of trajectory at its top point.
The correct Answer is:(a)h=√72+1)R,(b)1.13R
(a) Applying conservation of angular momentum between point P and Q
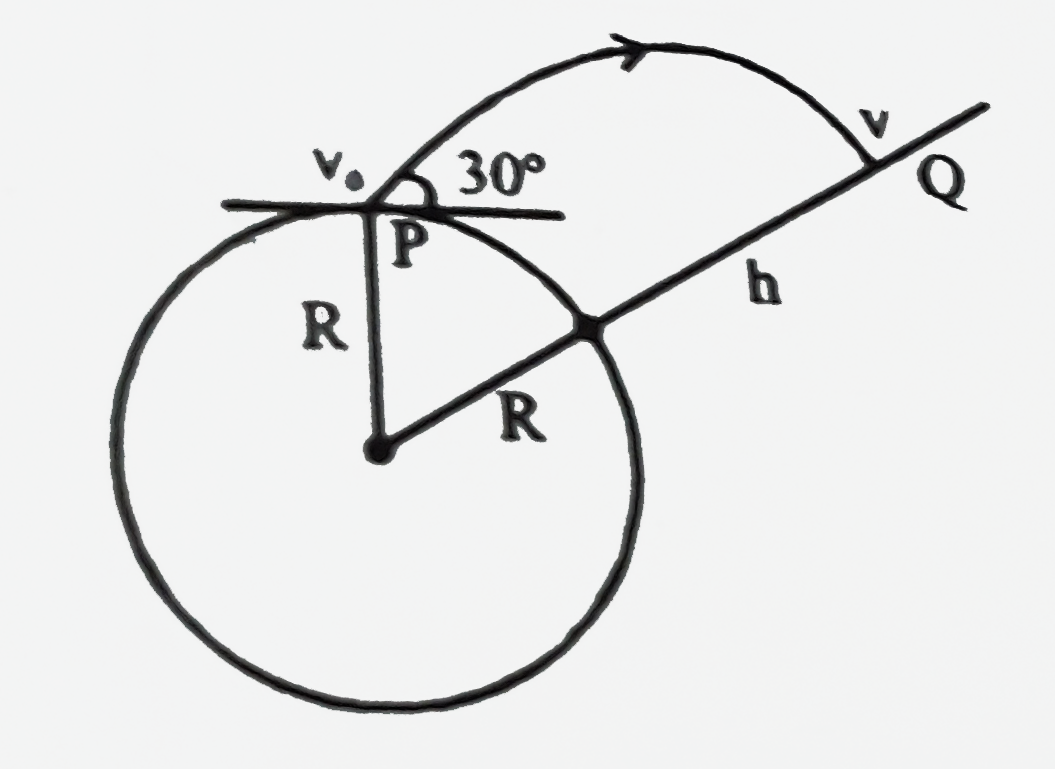
m(v0cos30∘)R=mvr
v=√32v0Rr...(1)
Applying conservation of mechanical energy.
−GMmR+12mv20=−GMmr+12mv2...(2)
From (1) and (2)
−GMmR+12mv20=−GMmr+12m3v20R24r2...(3)
given that v0=√32GMR...(4)
From (3) and (4)
4r2−16Rr+9R2=0
r=2R+√72R⇒R+h=2R+√72R
h=(√72+1)R⇒h=√72R
(b) Radius of curvature =v2g=(√3v0R2r2)2/GMR2
radius of curvature=34v20R2GM
=34×((32√GMR))2×R2GM=98R=1.125R
Similar Questions
A body is projected up from the surface of the earth with a velocity half the escape velocity at an angle of 30∘ with the horizontal. Neglecting air resistance and earth’s otation, find (a) the maximum height above the earth’s surface to which the body will rise. (b) will the body move around the earth as a satellite?
View SolutionA particle is fired vertically from the surface of the earth with a velocity kυe, where υe is the escape velocity and k<1. Neglecting air resistance and assuming earth's radius as Re. Calculated the height to which it will rise from the surface of the earth.
View Solution
Knowledge Check
If R is the radius of the earth, the height at which g will decrease by 0.1% of its value at the surface of the earth is
AR/6400BR/2000CR/1000DR/500STATEMENT-1: A body is projected from the ground with kinetic energy K at an angle of 60° with the horizontal. If air resistance is neglected, its K.E. When it is at the highest point of its trajectory will be K/4
because
STATEMENT-2: At the highest point of the trajectory, the direction of velocity and acceleration of the body are perpendicular to each otherAStatement-1 is True, Statement-2 is True, Statement -2 is a correct explanation for
Statement-1.BStatement-1 is True, Statement-2 is True, Statement -2 is NOT a correct explanation for
Statement-1CStatement - 1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.An object is projected from the earth's surface with escape velocity at 30∘ with horizontal. What is the angle made by the velocity with horizontal when the object reaches a height 2R from the earth's surface ? R is the radius of the earth. Horizontal can be considered as a line parallel to the tangent at the earth's surface just below the object .
A30∘B45∘C60∘D15∘
A projectile is fired from surface of earth at 30∘ above horizontal with speed u=√GMcR where Mc is mass of earth R is radius of earth Find maximum height of the projectile above earth surface
View SolutionA body is thrown from the surface of the Earth at an angle α to the horizontal with the initial velocity v0. Assuming the air drag to be negligible, find:
(a) the time of motion,
(b) the maximum height of ascent and the horizontal range, at what value of the angle α they will be equal to each other,
(c) the equation of trajectory y(x), where y and x are displacements of the body along the vertical and the horizontal respectively,
(d) the curvature radii of trajectory at its initial point and at its peak.
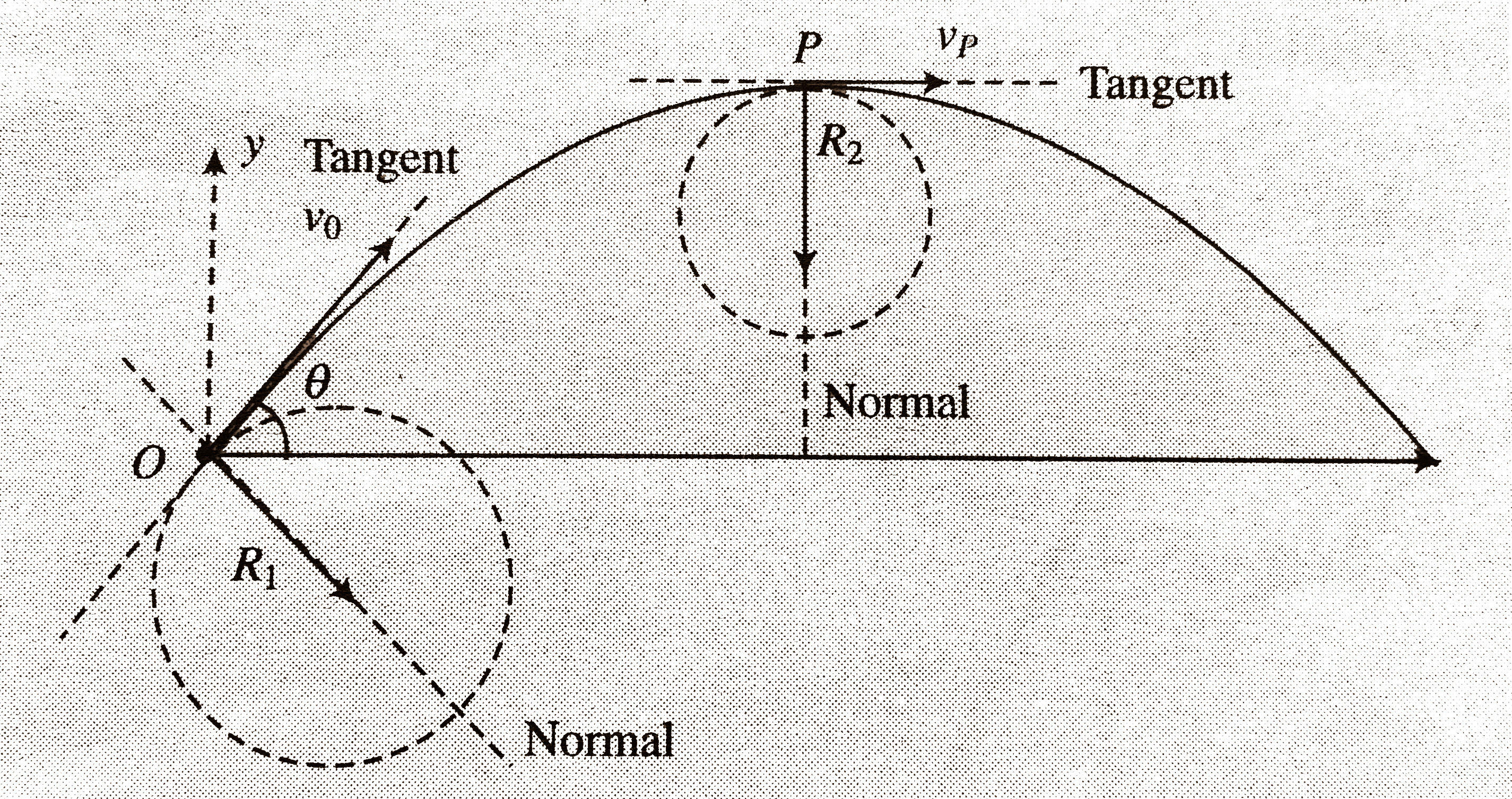
View SolutionA particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
 .
.
View SolutionA body is thrown with the velocity v0 at an angle of θ to the horizon. Determine v0inms−1 if the maximum height attained by the body is 5m and at the highest point of its trajectory the radius of curvature is r=3m. Neglect air resistance. [Use√80as9].
View SolutionA body Is projected horizontally near the surface of the earth with √1.5 times the orbital velocity. Calculate the maximum height up to which it will rise above the surface of the earth.
View Solution
