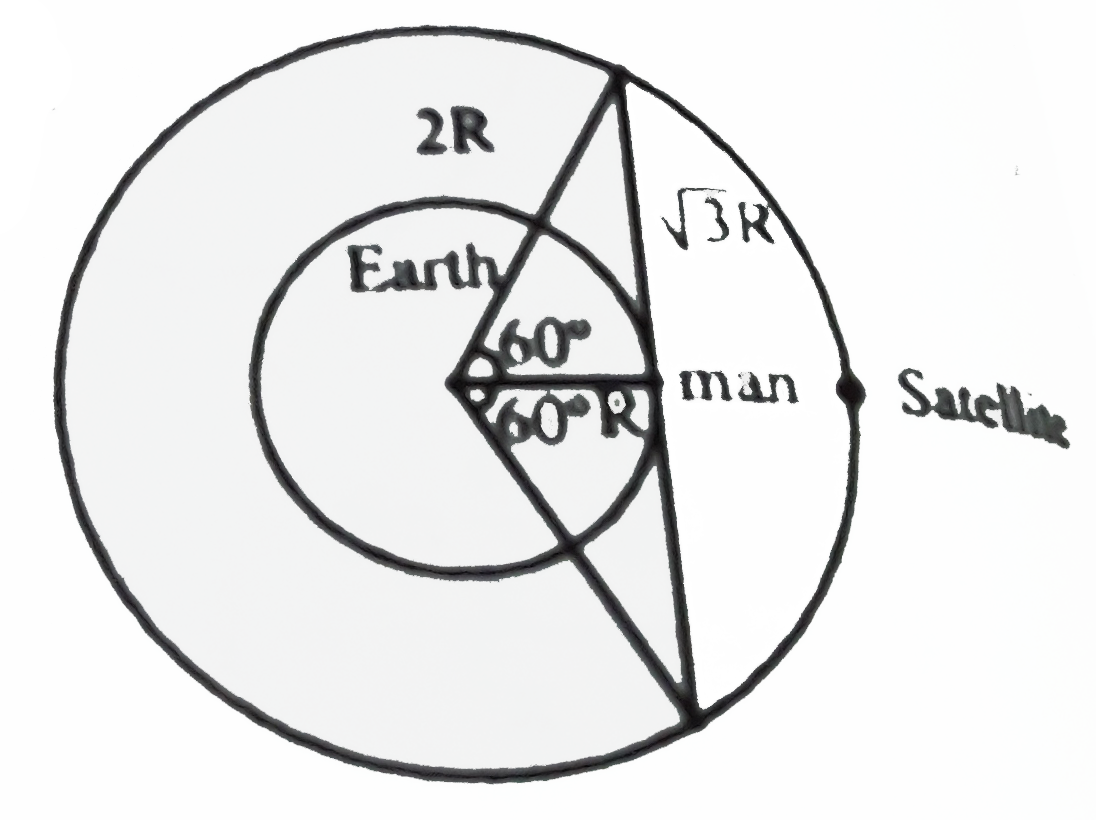
A satellite is orbiting the earth of mass $M$ in equatorial plane in a circular orbit having radius $2 R$ and same sense of rotation as that of the Earth. Find duration of time for which a man standing on the equator will be able tosee the satellite continuously. Assume that the mans can see the satellite when it is above horizon. take Earth's angular velocity $ω$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{2 π}{3 [\sqrt{\frac{G M}{8 R^{3}} - ω_{e}}]}$

Updated on:21/07/2023

Two satellites of masses M and 4M are orbiting the earth in a circular orbit of radius r. Their frequencies of revolution are in the ratio of
A $1 : 4$
B $4 : 1$
C $1 : 2$
D $1 : 1$
A satellite whose mass is M , is revolving in circular orbit of radius r around the earth. Time of revolution of satellite is
A $T \propto \frac{r^{5}}{G M}$
B $T \propto \sqrt{\frac{r^{3}}{G M}}$
C $T \propto \sqrt{\frac{r}{G M^{2} / 3}}$
D $T \propto \sqrt{\frac{r^{3}}{G M^{1} / 4}}$
A satellite of mass m moving around the earth of mass $m_{E}$ in a circular orbit of radius R has angular momentum L. The rate of the area swept by the line joining the centre of the earth and satellite is
AL/2m
BL/m
C2 L/m
D2L/ $m_{E}$