A hypothetical planet of mass M has three moons each of equal mass 'm' each revolving in the same circular orbit of radius R. The masses are equally spaced and thus form an equilateral triangle. Find :
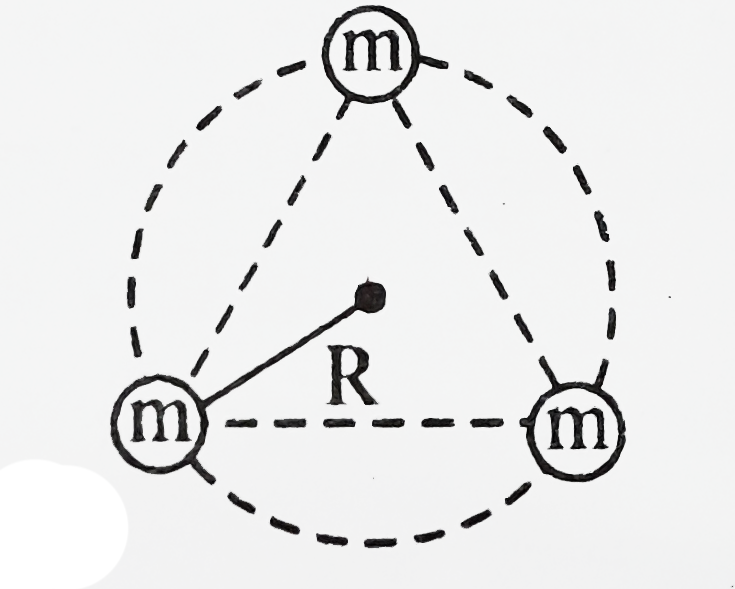
A hypothetical planet of mass M has three moons each of equal mass 'm' each revolving in the same circular orbit of radius R. The masses are equally spaced and thus form an equilateral triangle. Find : (i) the total P.E. of the system (ii) the orbital speed of each moon such that they maintain this configuration.
(i) the total P.E. of the system
(ii) the orbital speed of each moon such that they maintain this configuration.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:(i)−3GmR(m√3+M)⎞⎟⎠,(ii) ⎷GR(m√3+M)⎞⎟⎠

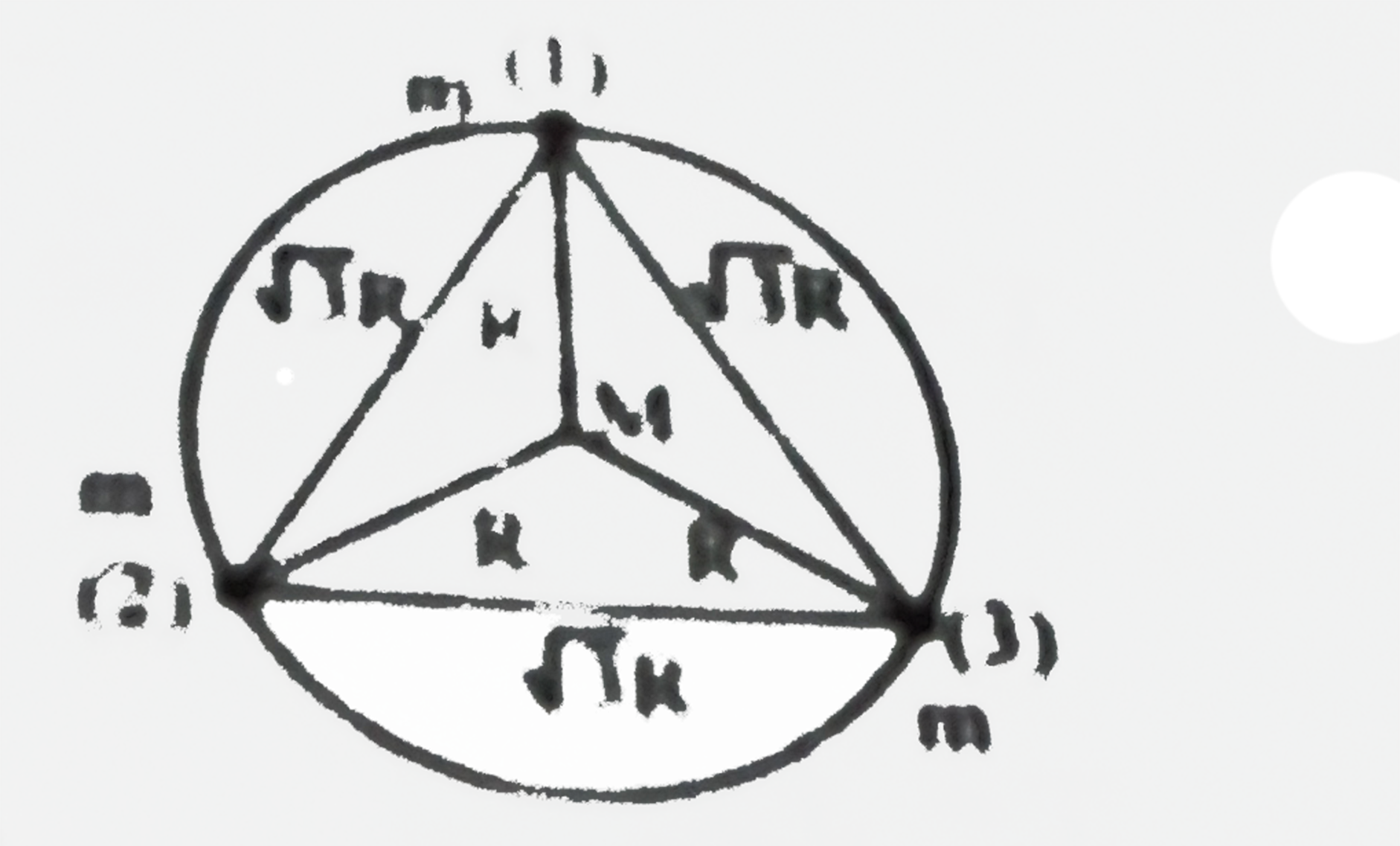
(i) U=potential energy of (1) in the fileld M+ potential energy of (2) in filed of [(1)+M]+potential energy of (3) in field of [(1)+(2)+M]
U=−GMmR+m[−GMR−Gm√3R]+m[−GmR−Gm√3R−Gm√3R]
=−2GMmR−3Gm2√3R
=−3GmR[M+m√3]
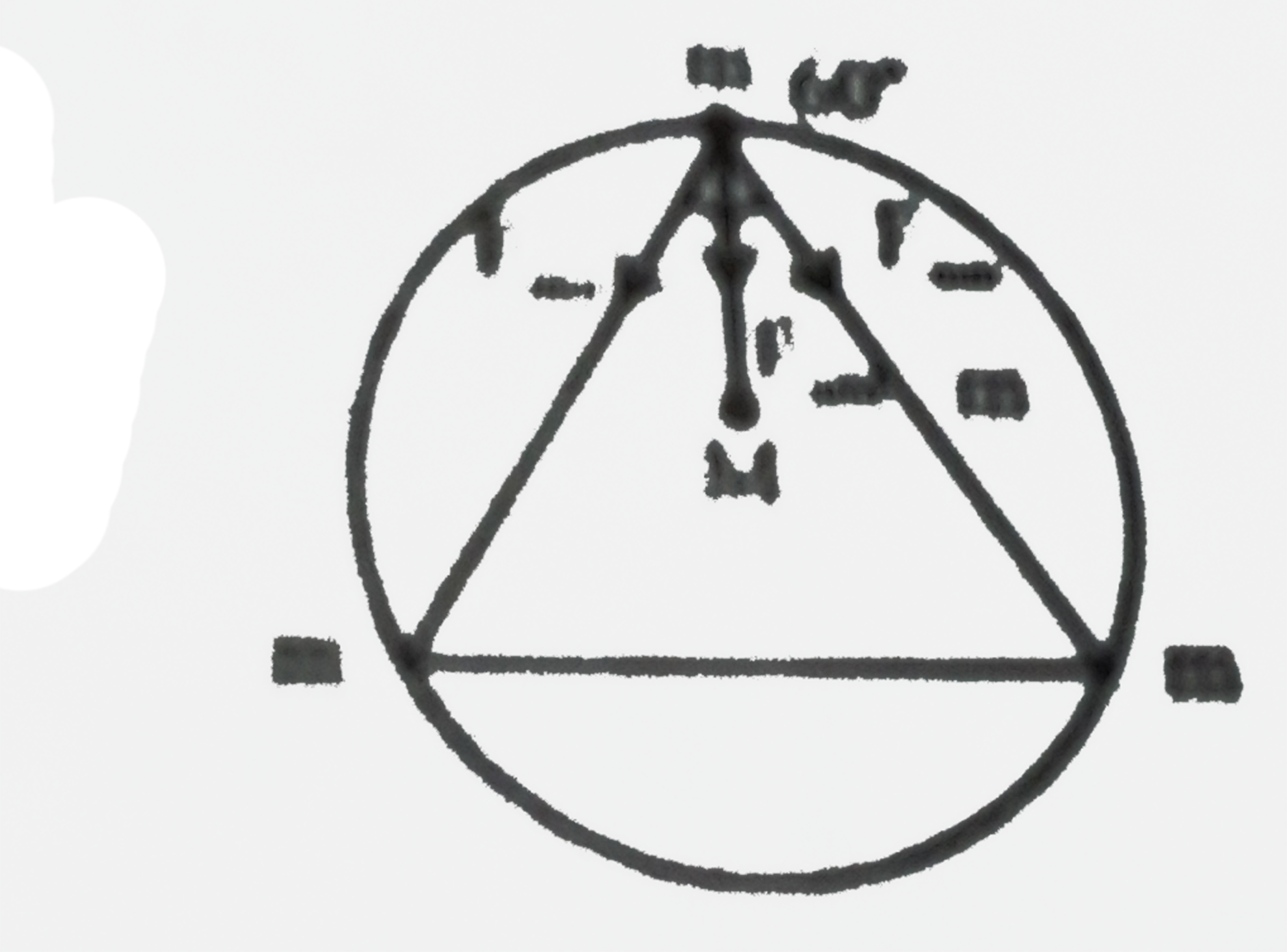
ocr_image
(ii)FR=FmM+2Fmmcos30∘
FR=GMmR2+√3Gm2(√3R)2
FR=GmR2[M+m√3]
This force will provided required centrepetal force
mv2R=GmR2[M+m√3]
v= ⎷GR(M+m√3)
ocr_image

Updated on:21/07/2023
|
Class 11PHYSICSGRAVITATION

Similar Questions

Knowledge Check

  • If a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is

    A4π2r3/GT
    B4π2r3/GT2
    C4π2r/GT
    D4π2r3/G2T2

  • A sayellite of mass m revolves in a circular orbit of radius R a round a planet of mass M. Its total energy E is :-

    A−GMm2R
    B+GMm3R
    C−GMmR
    D+GMmR

  • A planet of mass m is moving around a star of mass M and radius R in a circular orbit of radius r. The star abruplly shrinks to half its radius without any loss of mass. What change will be there in the orbit of the planet ?

    AThe planet will escape from the star
    BThe radius of the orbit will increase
    CThe radius of the orbit will decrease
    DThe radius of the orbit will not change