Two particles are in SHM in a straight line about same equilibrium position. Amplitude A and time period T of both the particles are equal. At time t=0, one particle is at displacement y1=+A and the other at y2=−A/2, and they are approaching towards each other. after what time they cross each other?
T/3
T/4
5T/6
T/6
The correct Answer is:D
To solve the problem step by step, we will analyze the motion of both particles in Simple Harmonic Motion (SHM) and determine when they cross each other.
Step 1: Understand the Initial Conditions
At time t=0:
- Particle 1 is at maximum displacement y1=+A.
- Particle 2 is at y2=−A2.
Step 2: Determine the Initial Phase Angles
For SHM, the displacement can be expressed as:
y=Asin(ωt+ϕ)
Where:
- ω=2πT is the angular frequency.
- ϕ is the phase constant.
For Particle 1:
- At t=0, y1=+A.
- Thus, Asin(ϕ1)=A implies ϕ1=π2 (90 degrees).
For Particle 2:
- At t=0, y2=−A2.
- Thus, Asin(ϕ2)=−A2 implies sin(ϕ2)=−12.
- This gives ϕ2=−π6 (or 210∘ in the unit circle).
Step 3: Write the Equations of Motion
The equations of motion for both particles can be written as:
1. For Particle 1:
y1(t)=Asin(ωt+π2)=Acos(ωt)
2. For Particle 2:
y2(t)=Asin(ωt−π6)
Step 4: Set Up the Condition for Crossing
The particles cross each other when their displacements are equal:
y1(t)=y2(t)
Substituting the equations:
Acos(ωt)=Asin(ωt−π6)
Step 5: Simplify the Equation
Dividing both sides by A (assuming A≠0):
cos(ωt)=sin(ωt−π6)
Using the identity sin(x)=cos(π2−x):
cos(ωt)=cos(π2−(ωt−π6))
This implies:
ωt=π2−(ωt−π6)+2nπ(for some integer n)
Step 6: Solve for Time
Rearranging gives:
2ωt=π2+π6+2nπ
2ωt=3π6+π6=4π6=2π3
Thus:
ωt=π3
t=π3ω
Since ω=2πT:
t=π3⋅T2π=T6
Final Answer
The two particles will cross each other after a time t=T6.
---
At time t=0:
- Particle 1 is at maximum displacement y1=+A.
- Particle 2 is at y2=−A2.
For SHM, the displacement can be expressed as:
y=Asin(ωt+ϕ)
Where:
- ω=2πT is the angular frequency.
- ϕ is the phase constant.
- At t=0, y1=+A.
- Thus, Asin(ϕ1)=A implies ϕ1=π2 (90 degrees).
- At t=0, y2=−A2.
- Thus, Asin(ϕ2)=−A2 implies sin(ϕ2)=−12.
- This gives ϕ2=−π6 (or 210∘ in the unit circle).
The equations of motion for both particles can be written as:
1. For Particle 1:
y1(t)=Asin(ωt+π2)=Acos(ωt)
y2(t)=Asin(ωt−π6)
The particles cross each other when their displacements are equal:
y1(t)=y2(t)
Substituting the equations:
Acos(ωt)=Asin(ωt−π6)
Dividing both sides by A (assuming A≠0):
cos(ωt)=sin(ωt−π6)
cos(ωt)=cos(π2−(ωt−π6))
This implies:
ωt=π2−(ωt−π6)+2nπ(for some integer n)
Rearranging gives:
2ωt=π2+π6+2nπ
2ωt=3π6+π6=4π6=2π3
Thus:
ωt=π3
t=π3ω
t=π3⋅T2π=T6
The two particles will cross each other after a time t=T6.
Similar Questions
Two particles are in SHM along same line with same amplitude A and same time period T. At time t=0, particle 1 is at + A2 and moving towards positive x-axis. At the same time particle 2 is at −A2 and moving towards negative x-axis. Find the timewhen they will collide.
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View Solution
Knowledge Check
Two particles are executing SHM in a straight line. Amplitude A and the time period T of both the particles are equal. At time t=0, one particle is at displacement x1=+A and the other x2=(−A2) and they are approaching towards each other. After what time they across each other? T4
AT3BT4C5T6DT6A particle starts SHM from the mean position. Its amplitude is A and time period is T. At the time when its speed is half of the maximum speed, its displacement y is
AA2BA√2CA√32D2A√3Time period (T) and amplitude (A) are same for two particle which undergoes SHM along the same line. At one particular instant one particle is at phase3π2and the other is at zero, while moving in the same direction. Find the time at which they will cross each other
A4T/2B3T/8C3T/4D3T/7
Two particles are in SHM with same amplitude A and same regualr frequency ω. At time t=0, one is at x =+A2 and the other is at x=−A2. Both are moving in the same direction.
View SolutionA particle starts its SHM from mean position at t=0. If its time period is T and amplitude A then the distance travelled by the particle in the time from t=0→t=5TA is
View SolutionA particle moves in a straight line and its position x and time t are related as follows: x=(2+t)1/2
Acceleration of the particle is given by
View SolutionTwo particles undergo SHM along the same line with the same time period (T) and equal amplitude (A). At a particular instant one particle is at x=−A and the other is at x = 0. They move in the same direction. They will cross each other at
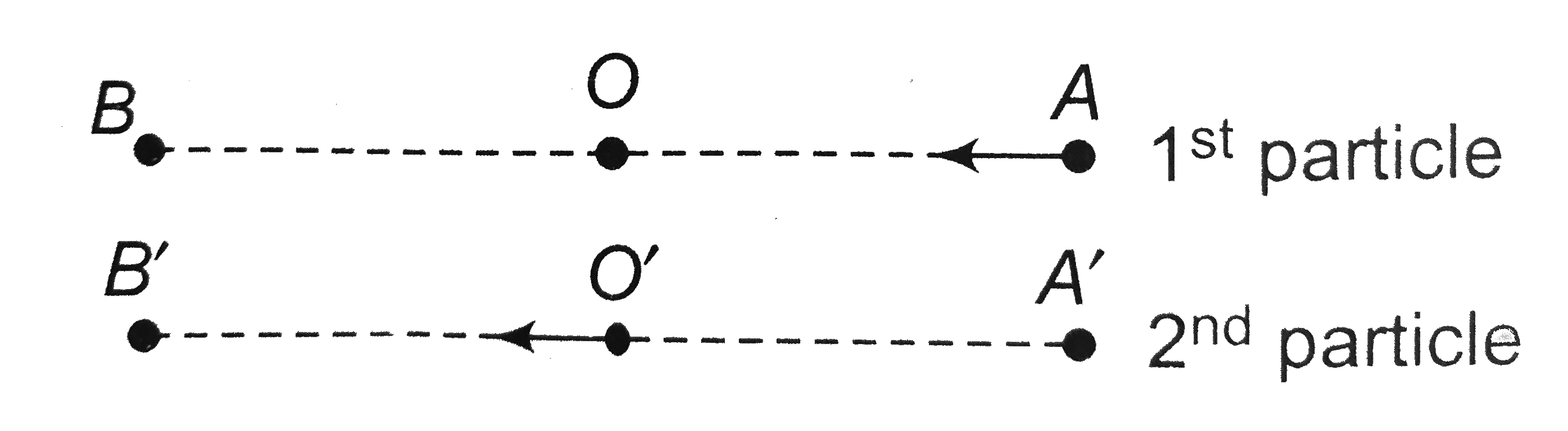
View SolutionTwo particle undergoes SHM along parallel line with the same time period (T) and equal amplitude At a particular instant , one particle is at its extereme position while the other is at its mean position .They move in the same direction .They will cross each other after a further time
View Solution