A ball moves over a fixed track as shown in the figure. From A to B ball rolls without slipping. Surface BC is frictionless. KA,KB and KC are kinetix energies of the ball at A,B and C, respectively. Then
 .
.
hA>hC,KB>KC
hA>hC,KC>KA
hA=hC,KB=KC
hA<hC,KB>KC
The correct Answer is:A, B
At AME=mghA…(1)
at BME−KB=Krotational(KC)….(2)
at CME=mghC,KB>KC
(B)hA>hC,KC>KA
On smooth part BC, due to zero torque, angular velocity and hence the rotational kinetic energy remains constant. While moving from B to translational kinetic energy converts into gravitational potential energy.
Similar Questions

A ball moves over a fixed track as shown in thre figure. From A to B the ball rolls without slipping. If surface BC is frictionless and KA,KB and KC are kinetic energies of the ball at A, B and C respectively then
(a). hA>hC,KB>KC
(b). hA>hC,KC>KA
(c). hA=hC,KB=KC
(d). hA<hC,KB>KC
View SolutionOne end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.
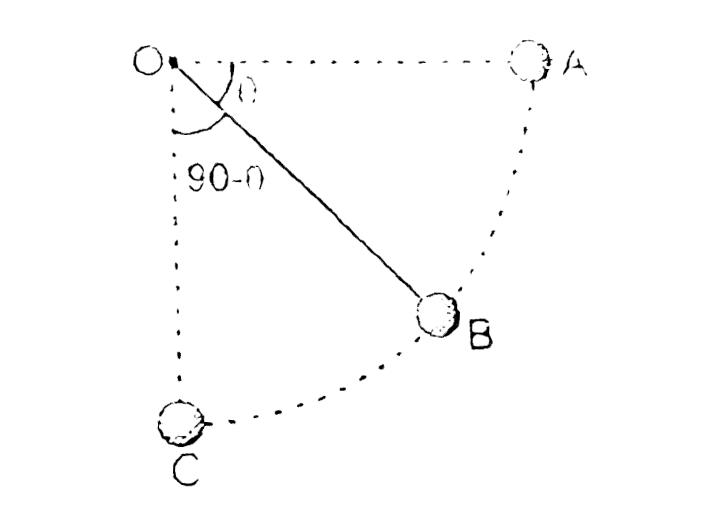
if |→vc|=2|→vB| then the value of θ shown is
View Solution
Knowledge Check
A ball moves over a fixed track as shown in the figure. From A and B the ball rolls without slipping. If surface B is frictionless and KA,KB and KC are kinetic energies of the ball at A,B and C respectively then:
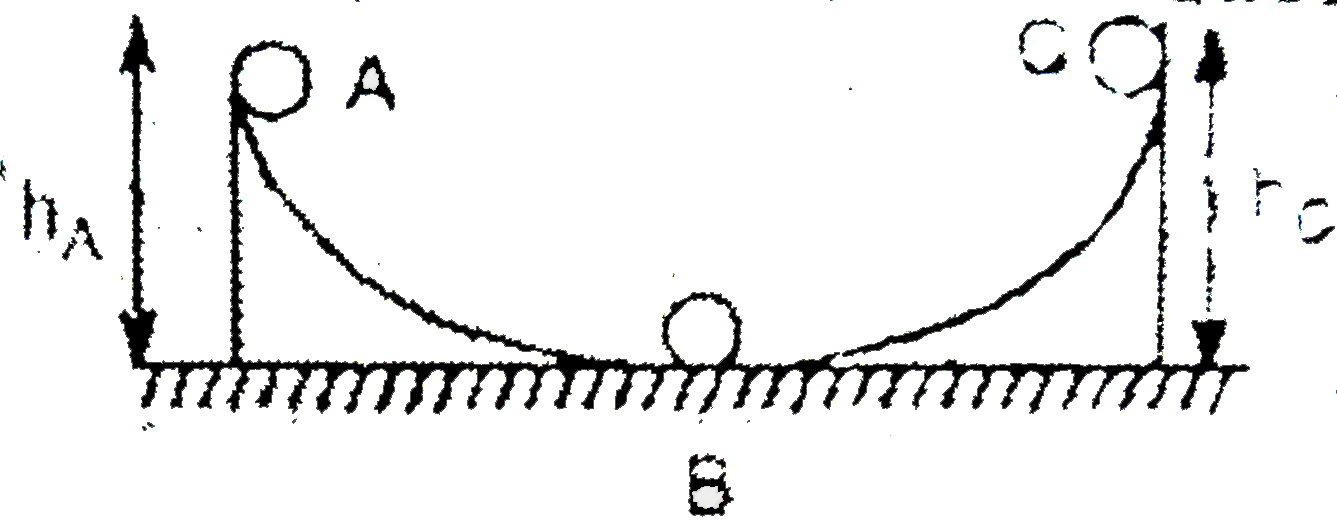 AhA>hC,KB>KCBhA>hC,KC>KAChA=hC,KB=KCDhA<hC,KB>KC
AhA>hC,KB>KCBhA>hC,KC>KAChA=hC,KB=KCDhA<hC,KB>KCA small bell starts moving from A over a fixed track as shown in the figure . Surface AB is friction from A to B the bell roll ralis without sipping BC is friction , KAKB andKC are kinetic energy of the bell at A,B and C respacecvely.Then
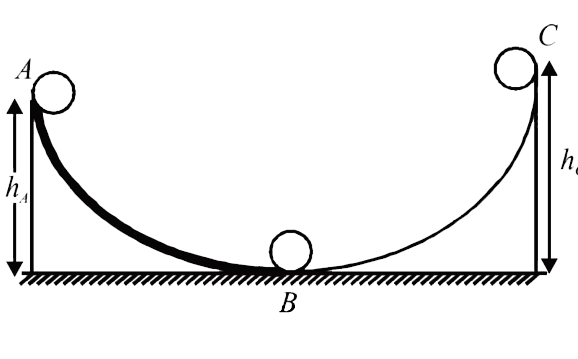 AhA>hC,KB>kcBhA>hC,Kc>kAChA=hC,KB>kcDhA<hC,KB>kc
AhA>hC,KB>kcBhA>hC,Kc>kAChA=hC,KB>kcDhA<hC,KB>kcA ball moves on a frictionless inclined table without slipping. The work done by the surface on the ball is :
APositiveBNegativeCZeroDNone of these
One end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.

If |→vc|=2|→vB| then
View SolutionA ball moves along a curved path of radius 5m as shown in figure. It starts from point A and reaches the point B. Calculate the normal force that acts on the ball at B, assuming that there is no friction between the ball and the surface of contact.
View Solution(i) Three balls 1, 2 and 3 lie on a smooth horizontal table. Ball 1 is given a velocity towards ball 2. Kinetic energy given to ball 1 is k0. It collides with 2 and in turn ball 2 hits ball 3. All collisions are head on elastic. Masses of the balls are m, M and m respectively.
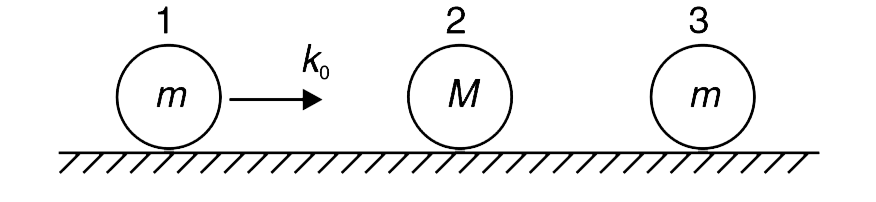
(a) Calculate the kinetic energy (k3) of ball 3 after ball 2 hits it.
(b) Draw the variation of k3 as a function of M.
(ii) Consider 10 balls laid on a smooth surface with masses m,m2,m4,m8......m512 and first ball is pushed towards the second with kinetic energy k0. [All collisions are elastic and head on]. The kinetic energy acquired by the last ball is k10. In a separate experiment the 10th ball is pushed towards 9th ball with kinetic energy k0. This time the kinetic energy acquired by 1st ball is k1.
Compare k10andk1

View SolutionAssuming a ball of mass m and of radius r to roll down from the top without slipping. Neglect energy losses due to rolling friction.
View SolutionA sphere is rolling on a horizontal surface without slipping. The ratio of the rotational K.E. to the total kinetic energy of the sphere is
View Solution
