A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radus R is placed horizontally at rest its length parallel to the edge such that the exis of the cylinder and the endg of the block are in the same vertical plane as shown in the figure below. Ther is sufficinet friction present at the edge s that a very small displacement causes the cylinder to roll off the edge without slipping. Determine:

(a) the angle θc through which the cylinder rotates before it leaves contact with the edge,
(b) the speed of the centre of mass of the cylinder before leaving contact with the edge, and
(c) the ratio of the translational to rotational kinetic energy of the cylinder when its centre of mass is in horizontal line with the edge.
The correct Answer is:(a) θC=cos−1(4/7),
(b) v=√4/7gR
( c) KT/KR)=6.
(a) The cylinder rotates about the point of contact. Hence, the mechanical energy of the cylinder will be conserved i.e.

:. PEi+KEi=PEf+KEf
:. mgR+0+mgRcosθ+Iω2+12mv2
but ω=v/R (No slipping at point of contact)
and I=12mR2
Therefore,

mgR=mgRcosθ+12(12mR2)(v2R2)+12mv2
v2R=43g(1−cosθ)...(1)
At the time of leaving contact, normal reaction N=0 and θ=θC, hence
mgcosθC=mv2)R
v2R=gcosθC...(2)
From Eqs. (1) and (2),
43g(1−cosθC)=gcosθC
cosθC=4/7⇒θC=cos−1(4/7)
(b) v=√43gR(1−cosθ) From Eq. (1)
At the time of loosing contact
cosθC=47
:. v=√43gR(1−47)or v=√47gR
( c) At the moment, when cylinder looses contact
v=√47gR Therefore, KR=12Iω2
KR=12(12mR2)v2R2⇒KR=14mv2
KR=12(47gR)⇒KR=mgR7....(3)
Now, once the cylinder losses its contact, N=0, i.e. the frictional force, which is responsible for its rotation, also vanishes. Hence its rotation a kinetic energy now becomes constant, while its translational kinetic energy increases.
KEtranslational=DecreaseinPEgravitational−KR ....(4)
KT=(mgR)−mgR7⇒KT=67mgR
From Eqs, (3) and (4)
KTKR=67mgRmgR7 or KTKR=6.
Similar Questions
A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radus R is placed horizontally at rest its length parallel to the edge such that the exis of the cylinder and the endg of the block are in the same vertical plane as shown in the figure below. Ther is sufficinet friction present at the edge s that a very small displacement causes the cylinder to roll off the edge without slipping. Determine:

(a) the angle θc through which the cylinder rotates before it leaves contact with the edge,
(b) the speed of the centre of mass of the cylinder before leaving contact with the edge, and
(c) the ratio of the translational to rotational kinetic energy of the cylinder when its centre of mass is in horizontal line with the edge.
View SolutionTotal number of edges a cylinder has
View Solution
Knowledge Check
A clockwise torque of 6N−m is applied to the circular cylinder as shown in the figure. There is no friction between the cylinder and the block.
 AThe cylinder will be slipping but the system does not move forwardBThe system cannot move forward for any torque applied to the cylinderCThe acceleration of the system will be 1m/s2 forwardDThe angular acceleration of the cylinder is 10rads−2
AThe cylinder will be slipping but the system does not move forwardBThe system cannot move forward for any torque applied to the cylinderCThe acceleration of the system will be 1m/s2 forwardDThe angular acceleration of the cylinder is 10rads−2A hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
AZeroB2πRLEC2πR2EDE . AA hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
AZeroB2πRLEC2πR2EDE . A
Show that a nonhomogeneous cylinder on a horizontal plane has a position of stable equilibrium when its centre of gravity is vertically below the axis O of the cylinder.
View SolutionAB is a non uniform plank of length L=4R with its centre of mass at C such that AC=R. It is placed on a step with its one end A supported by a cylinder of radius R as shown in figure. The centre of mass of the plank is just outside the edge of the step. The cylinder is slowly rolled on the lower step such that there is no slipping at any of its contacts. Calculate the distance through which the centre of the cylinder moves before the plank loses contact with the horizontal surface of the upper step.

View Solution
A cylinder of mass M and radius R is resting on two corner edges A and B as shown in figure. The normal reaction at the edges A and B are: (Neglect friction)
View SolutionA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
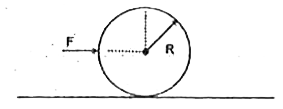
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View Solution