A ladder of length L is slipping with its ends against a vertical wall and a horizontal floor. At a certain moment, the speed of the end in contact with the horizontal floor is v and the ladder makes an angle θ=30∘ with horizontal. Then, the speed of the ladder's centre of mass must be
2v/√3
v/2
v
None
The correct Answer is:C
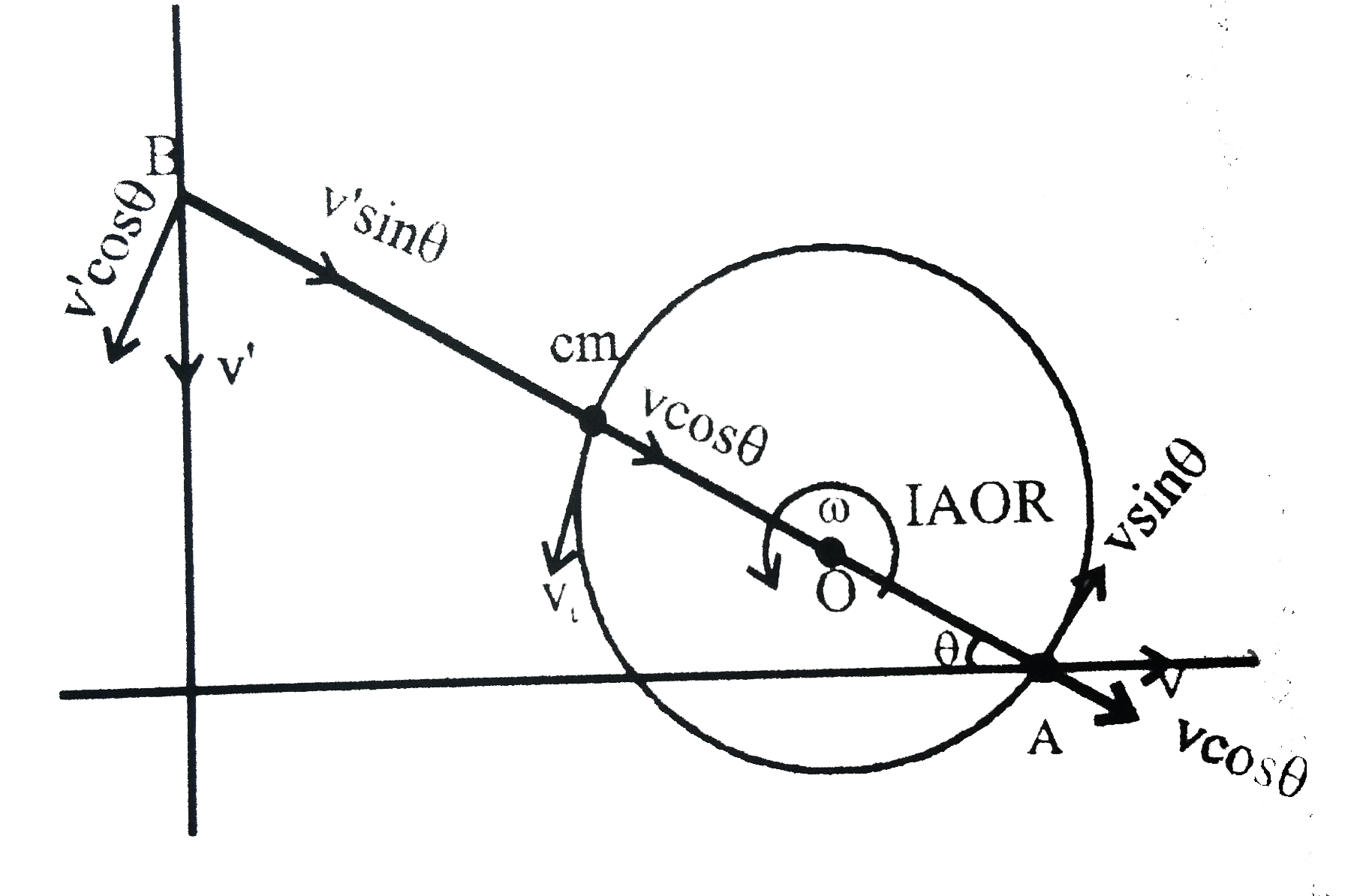
v'sinθ=vcosθ
v'=vtanθ⇒v'=√3v….(1)
let instantaneous axis of rotation is at distance l frome end A.
ω=vsinθl=v'cosθ(L−l)⇒ω=vsin30∘l=v'cos30∘(L−l)
ω=v2l=v'√32(L−l)....(2)
from (1) m & (2)
vl=√3v(L−l)⇒l=L4
by putting the value of l in equation (2)ω=2vL
tangential velocity of c.m.vt=L4ω
vt=v2⇒vcm=√v2t+(vcosθ)2
vcm
⎷(v2)2+(√3v2)2⇒vcm=v.
Similar Questions
A ladder is resting with one end on a vertical wll and the other end on a horizontal floor. Is it more likely to slip when a man stnads near the bottom or near the top?
View SolutionA ladder of length 50 m rests against a vertical wall, at a height of 30 m from the ground. Find the inclination of the ladder with the horizontal. Also find the distance between the foot of the ladder and the wall.
View Solution
Knowledge Check
A stone is thrown with a velocity v at an angle θ with the horizontal.Its speed when it makes an angle β with the horizontal is
AvcosθBvcosβCvcosθcosβDvcosθcosβA ladder 20 ft long leans against a vertical wall. The top end slides downwards at the rate of 2 ft per second. The rate at which the lower and moves on a horizontal floor when it is 12 ft from the wall is
A83B65C32D174A ladder rests against a vertical wall at angle α to the horizontal . If is foot is pulled away from the wall through a distance 'a' so that it slides a distance 'b' down the wall making the angle β with the horizontal , then a =
Abtan(α−β2)Bbtan(α+β2)Cbcot(α−β2)Dnone of these
A ladder 12 units long slides in a vertical plane with its ends in contact with a vertical wall and a horizontal floor along x-axis. The locus of a point on the ladder 4 units from its foot has the equation:
View SolutionA rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle θ with the vertical.
View Solution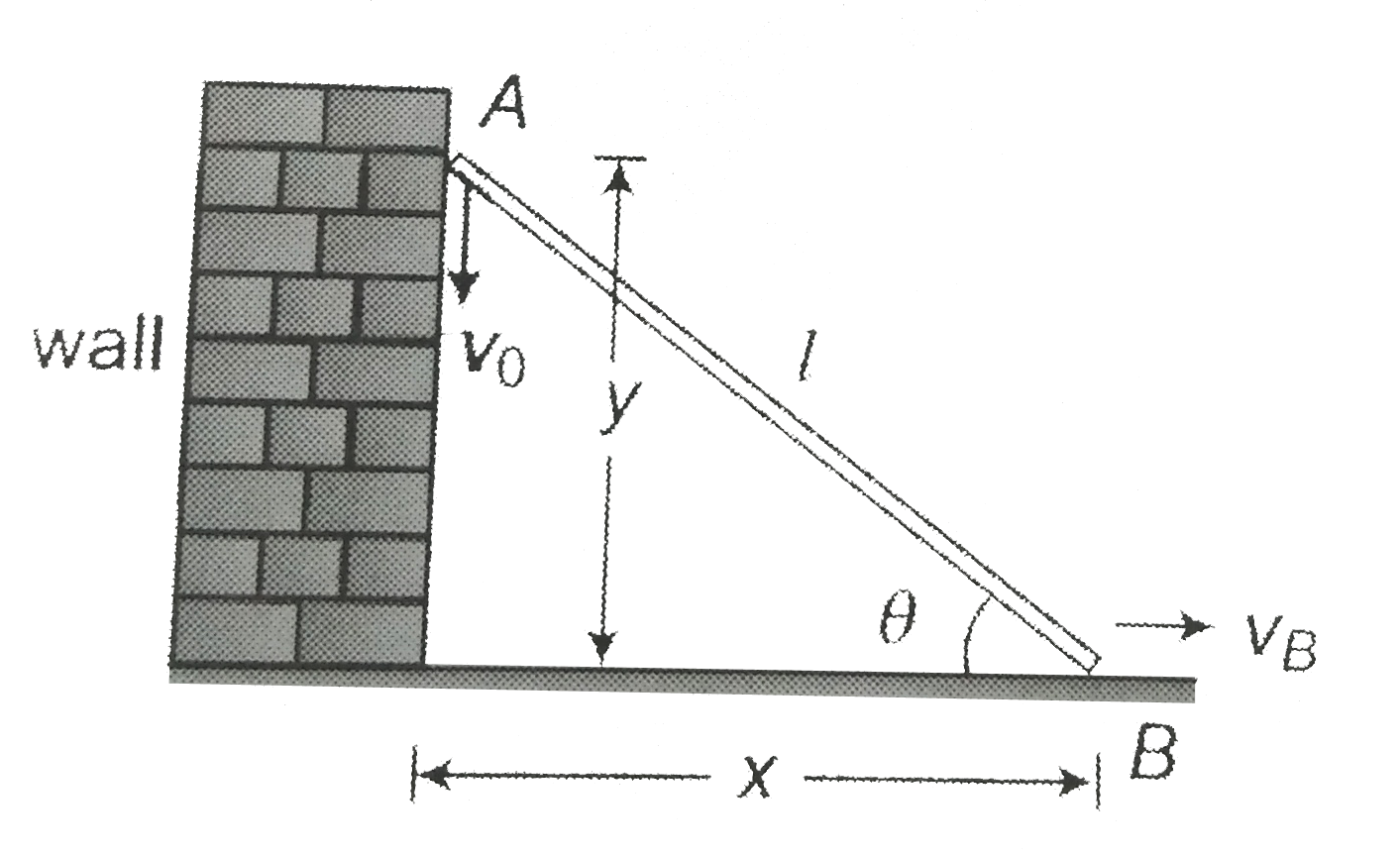
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View Solution(i) A uniform ladder of length L and weight w rests against a vertical wall and makes an angle θ with the horizontal ground. If the coefficient of friction at the point of contact of the ladder with the wall and ground is μ, show that the greatest height x, measured along the ladder from the foot to which a man of weight w may climb without the ladder slipping is given by
xL=μ(W+w)W(1+μ2)(μ+tanθ)−w2W
(ii) If the wall be smooth and coefficient of friction between ladder and ground be 0.25, show that
x=L4(1−wW)tanθ−wL2W
View Solution