A parojectile of mass 1kg is projected with a velcoity of √20m/s such that it strikes on the same level as the point of projection at a distance of √3m. Which of the following options are incorrect:
The maximum height reached by the projectile can be 0.25m.
the minimum velocity during its motion can be √15m/s
the time taken for the flight can be √35sec.
maximum potential enegry during its motion can be 6J.
The correct Answer is:D
To solve the problem, we need to analyze the projectile motion of the given object and determine which of the provided options are incorrect. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Given Information
- Mass of the projectile (m) = 1 kg
- Initial velocity (u) = √20 m/s
- Range (R) = √3 m
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Use the Range Formula
The range of a projectile is given by the formula:
R=u2sin(2θ)g
Substituting the known values:
√3=(√20)2sin(2θ)10
√3=20sin(2θ)10
√3=2sin(2θ)
sin(2θ)=√32
Step 3: Find Possible Angles
From the sine value, we can find:
2θ=60∘ or 120∘
Thus,
θ=30∘ or 60∘
Step 4: Calculate Maximum Height
Using the formula for maximum height H:
H=u2sin2(θ)2g
For θ=30∘:
H=(√20)2sin2(30∘)2×10
H=20×(12)220=0.25 m
For θ=60∘:
H=(√20)2sin2(60∘)2×10
H=20×(√32)220=0.75 m
Step 5: Calculate Time of Flight
The time of flight T is given by:
T=2usin(θ)g
For θ=30∘:
T=2×√20×sin(30∘)10
T=2×√20×1210=√2010=√2010=2√510=√55 seconds
For θ=60∘:
T=2×√20×sin(60∘)10
T=2×√20×√3210=√20√310=√6010=√155 seconds
Step 6: Calculate Maximum Potential Energy
The maximum potential energy (PE) at the maximum height is given by:
PE=mgh
For θ=30∘:
PE=1×10×0.25=2.5 joules
Step 7: Evaluate the Options
1. Maximum height raised by the projectile can be 0.25 meters. (Correct)
2. Minimum velocity during its motion can be √15 m/s. (Incorrect)
3. Time taken for the flight can be √35 seconds. (Correct)
4. Maximum potential energy during its motion can be 6 joules. (Incorrect)
Conclusion
The incorrect options are:
- Minimum velocity during its motion can be √15 m/s.
- Maximum potential energy during its motion can be 6 joules.
- Mass of the projectile (m) = 1 kg
- Initial velocity (u) = √20 m/s
- Range (R) = √3 m
- Acceleration due to gravity (g) = 10 m/s²
The range of a projectile is given by the formula:
R=u2sin(2θ)g
Substituting the known values:
√3=(√20)2sin(2θ)10
√3=20sin(2θ)10
√3=2sin(2θ)
sin(2θ)=√32
From the sine value, we can find:
2θ=60∘ or 120∘
Thus,
θ=30∘ or 60∘
Using the formula for maximum height H:
H=u2sin2(θ)2g
H=(√20)2sin2(30∘)2×10
H=20×(12)220=0.25 m
H=(√20)2sin2(60∘)2×10
H=20×(√32)220=0.75 m
The time of flight T is given by:
T=2usin(θ)g
T=2×√20×sin(30∘)10
T=2×√20×1210=√2010=√2010=2√510=√55 seconds
T=2×√20×sin(60∘)10
T=2×√20×√3210=√20√310=√6010=√155 seconds
The maximum potential energy (PE) at the maximum height is given by:
PE=mgh
For θ=30∘:
PE=1×10×0.25=2.5 joules
1. Maximum height raised by the projectile can be 0.25 meters. (Correct)
2. Minimum velocity during its motion can be √15 m/s. (Incorrect)
3. Time taken for the flight can be √35 seconds. (Correct)
4. Maximum potential energy during its motion can be 6 joules. (Incorrect)
The incorrect options are:
- Minimum velocity during its motion can be √15 m/s.
- Maximum potential energy during its motion can be 6 joules.
Similar Questions
The particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
View SolutionA projectile thrown from a height of 10 m with velocity of √2m/s the projectile will fall, from the foot of projection, at distance- (g=10m/s2)
View Solution
Knowledge Check
A particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
Adisplacement of particle is 100mBvertical component of velocity is 20m/sCvelocity makes an angle tan−1(2) with verticalDparticle is at height of 60m from groundA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
Angular velocity of rod after collision is
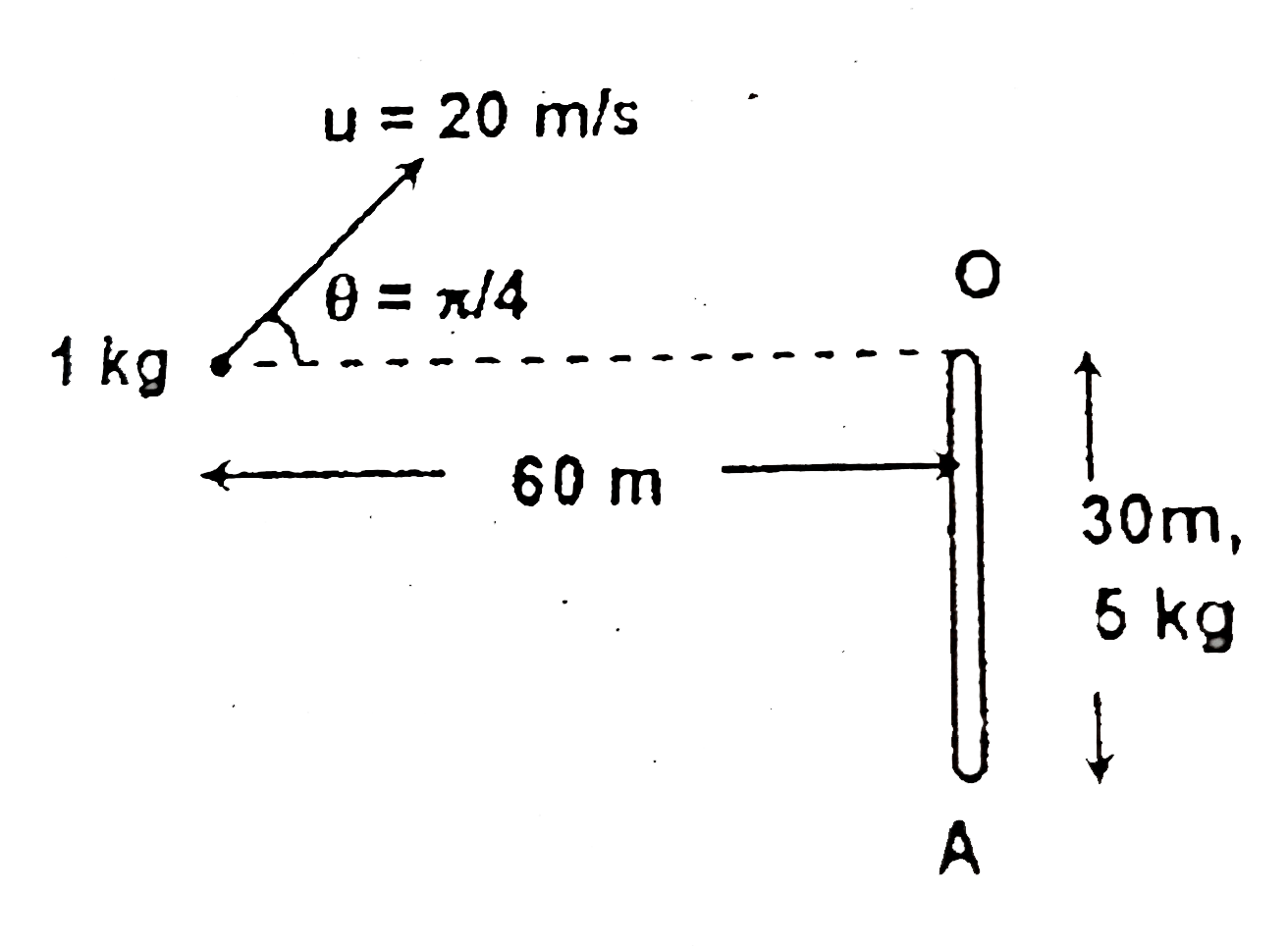 A14√2rad/secB4√2rad/secC4√2rad/secDzero
A14√2rad/secB4√2rad/secC4√2rad/secDzeroA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If the rod tilts to an angle θ after collision, then
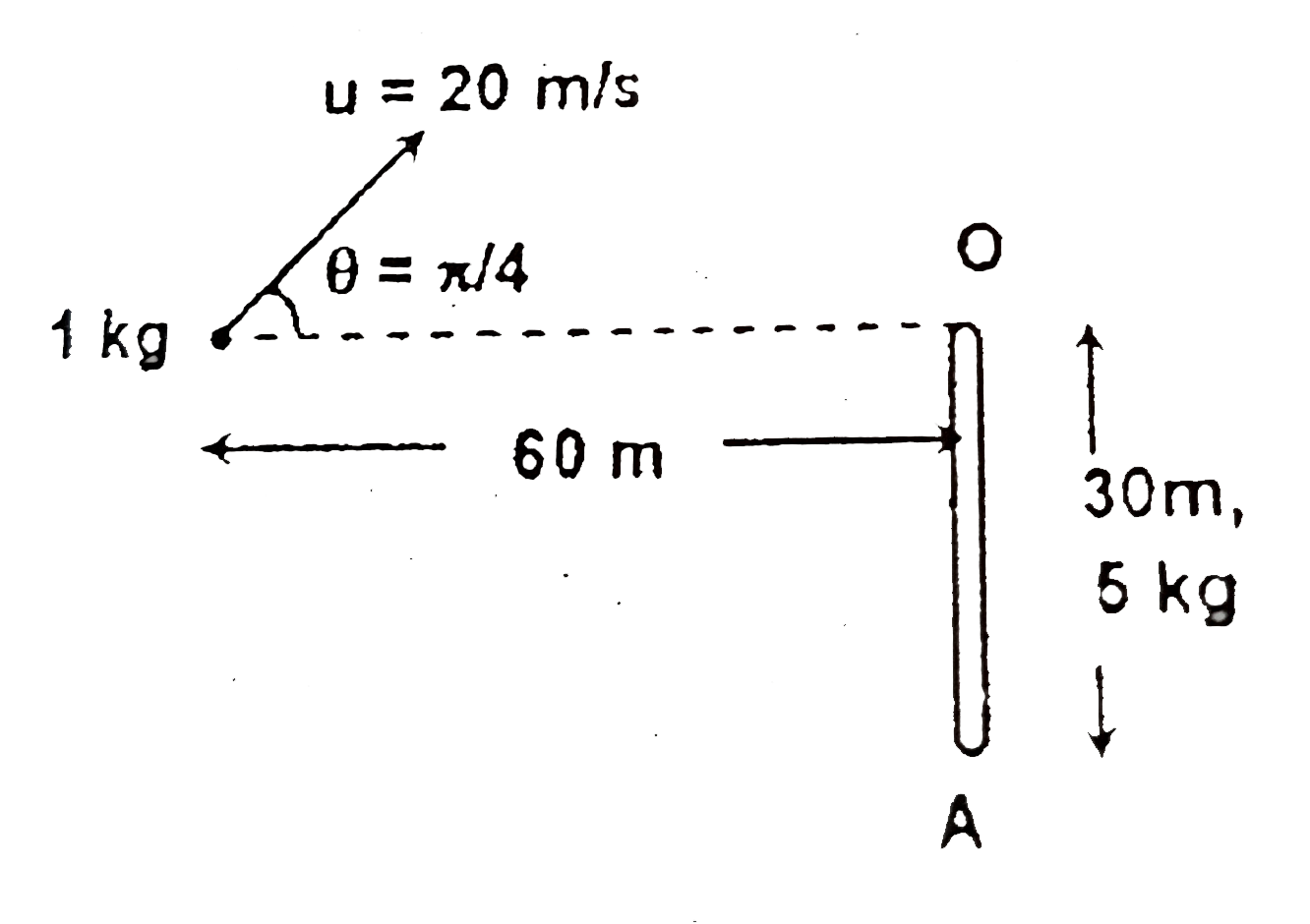 Aθ=0∘Bθ=cos−1(40/42)Cθ=cos−1(41/42)Dθ=cos−1(27/28)
Aθ=0∘Bθ=cos−1(40/42)Cθ=cos−1(41/42)Dθ=cos−1(27/28)
A particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s(g=10m/s2) match the following table
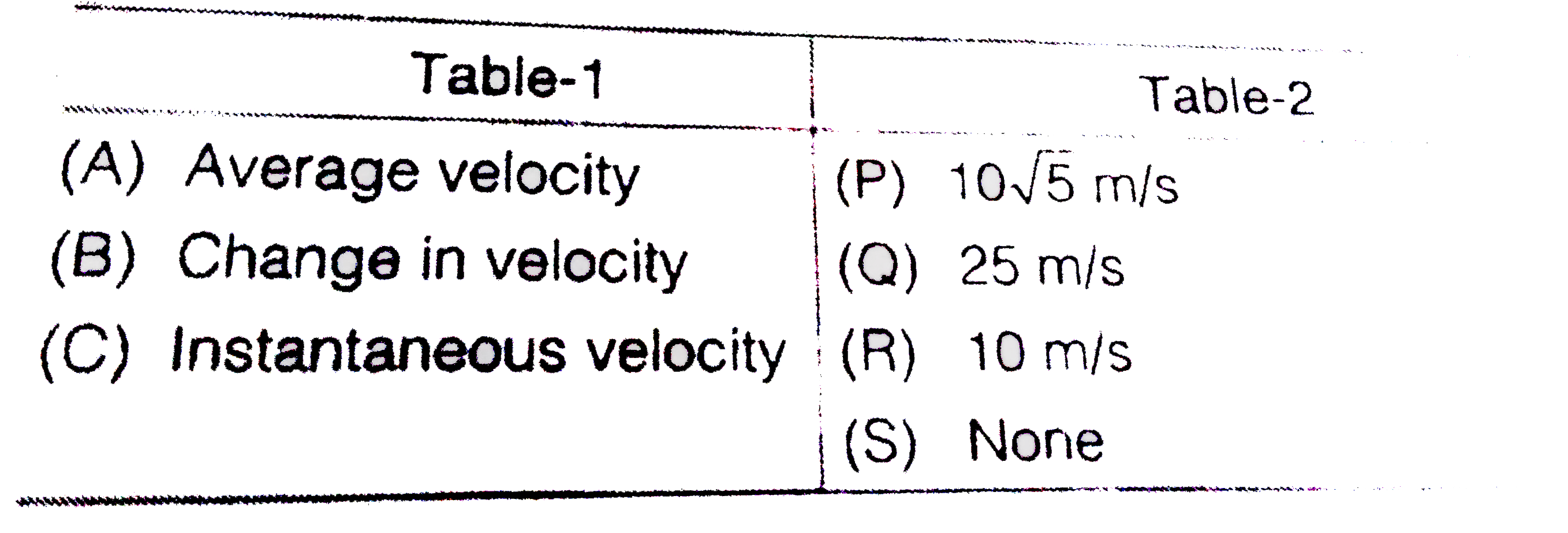
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA ball is projected vertically upward with a velocity 112m/s The time taken by it to return to the point of projection is (g=10m/s2) :
View SolutionA ball is projected vertically upward with a velocity 112m/s The time taken by it to return to the point of projection is (g=10m/s2) :
View SolutionA projectile of mass 3m is projected from ground with velocity 20√2m/s at 45∘. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of 100m from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
(g=10m/s2)
View Solution