An object is moving along the xaxis with postion as a function of time given by x=x(t). Point O is at x=0. Object is definitely moving towardr O when
dx/dt<0
dx/dt>0
dx2/dt2<0
dx2/dt2>0
The correct Answer is:C
To determine when an object is moving towards point O (the origin at x=0), we need to analyze its position function x(t) and its velocity v(t).
1. Understanding the Position Function:
The position of the object is given by x(t), which indicates its location along the x-axis at any time t.
2. Defining Movement Towards the Origin:
The object is moving towards the origin if its position x(t) is decreasing over time, meaning it is getting closer to x=0.
3. Velocity Calculation:
The velocity v(t) of the object is the derivative of the position function with respect to time:
v(t)=dxdt
4. Condition for Moving Towards the Origin:
For the object to be moving towards the origin, the following condition must hold:
- If x(t)>0 (the object is to the right of the origin), then v(t)<0 (the object must be moving left).
- If x(t)<0 (the object is to the left of the origin), then v(t)>0 (the object must be moving right).
5. Combining Conditions:
We can express this mathematically:
x(t)⋅v(t)<0
This means that the position x(t) and the velocity v(t) must have opposite signs for the object to be moving towards the origin.
6. Conclusion:
Therefore, the object is definitely moving towards point O when the product of its position and velocity is negative:
x(t)⋅dxdt<0
The position of the object is given by x(t), which indicates its location along the x-axis at any time t.
The object is moving towards the origin if its position x(t) is decreasing over time, meaning it is getting closer to x=0.
The velocity v(t) of the object is the derivative of the position function with respect to time:
v(t)=dxdt
For the object to be moving towards the origin, the following condition must hold:
- If x(t)>0 (the object is to the right of the origin), then v(t)<0 (the object must be moving left).
- If x(t)<0 (the object is to the left of the origin), then v(t)>0 (the object must be moving right).
We can express this mathematically:
x(t)⋅v(t)<0
This means that the position x(t) and the velocity v(t) must have opposite signs for the object to be moving towards the origin.
Therefore, the object is definitely moving towards point O when the product of its position and velocity is negative:
x(t)⋅dxdt<0
Similar Questions
A particle is moving along x axis. Its position as a function of time is given by x=x(t). Say whether following statements are true or false.
(a) The particle is definitely slowing down if d2xdt2>0 and dxdt<0
(b) The particle is definitely moving towards the origin if d(x2)dt<0
View SolutionAn object is moving along +ve x-axis with a uniform acceleration of 4ms−2 . At time t=0 , x=5m and v=3ms−1 .
(a) What will be the velocity and position of the object at time t=2s?
What will be the velocity and position of the object when it has a velocity of 5ms−1?
View Solution
Knowledge Check
An object is moving in the x-y plane with the position as a function of time given by →r=x(t)ˆi+y(t)ˆj. Point O is at x=0,y=0 . The object is definitely moving towards O when
Avx>0,vy>0Bvx<0,vy<0Cxvx+yvy<0Dxvx+yvy>0Figure shows the position of a particle moving on the X-axis as a function of time.
 AThe particle has come to rest 6 timesBThe maximum speed is at t=6 s.CThe velocity remains positive for t=0 to t=6s.DThe average velocity for the total period shown is negative
AThe particle has come to rest 6 timesBThe maximum speed is at t=6 s.CThe velocity remains positive for t=0 to t=6s.DThe average velocity for the total period shown is negativeFigure shows the position of a particle moving on the x - axis as a function of time
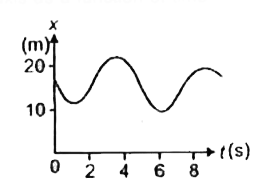 AThe particle has come to rest 4 timesBThe velocity at t = 8 s is negativeCThe velocity remains positive for t = 2 s to t = 6 sDThe particle moves with constant velocity.
AThe particle has come to rest 4 timesBThe velocity at t = 8 s is negativeCThe velocity remains positive for t = 2 s to t = 6 sDThe particle moves with constant velocity.
An object is moving along+ve x-axis with a uniform acceleration of 4 ms^(-2).Attime t=0.X=4m and v=2ms−1.<br>(a)Wˆwillbethevelocityandpositionoftheobjectattime t=3 s?
(b) What will be the position of the object when it has a velocity 8ms−1 ?
View SolutionA particle moves along the x-axis so that its position is given x=2t3–3t2 at a time t second. What is the time interval duringwhich particle will be on the negative half of the axis?
View SolutionThe particle is moving such that its displacement along x-axis as a function of time is given by x(x−6)=1−10cosωt. Find amplitude, time period and mean position.
View SolutionA point moves such that its displacement as a function of times is given by x2=t2+1. Its acceleration at time t is
View SolutionA point moves such that its displacement as a function of time is given by x3=r3+1. Its acceleration as a function of time t will be
View Solution
