When a resistance R is connected in series with an element A, the electric current is found to be lagging behind the voltage by angle θ1. When the same resistanceis connected in series with element B, current leads voltage by θ2. When R, A, B are connected in series, the current now leads voltage by theta. Assume same AC source is used in all cases, then:
θ=θ2−θ1
tanθ=tanθ2−tanθ1
θ=θ1+θ22
none of these
The correct Answer is:B
tanθ1=XLR…(1)
tanθ2=XCR…(2)
tanθ=XC−XLR
tanθ=XCR−XLR…(3)
from (1),(2) and (3)tanθ=tanθ2−tanθ1
Similar Questions
Knowledge Check
In an AC circuit, a resistance R is connected in series with an inductance L. If the phase angle between the voltage and the current is pi//4 then the value of ihe inductive reactance is
AR/4BR/2CRDR/sIn a circuit L, C and R are connected in series with an alternating voltage source of frequency f. The current leads the voltage by 45∘. The value of C is
A1πf(2πfL−R)B12π(2πfL−R)C1πf(2πfL+R)D12π(2πfL+R)In a circuit L,C and R are connected in series with an alternating voltage source of frequency f. The current lead the voltages by 45∘. The value of C is :
A12πf(2πfL−R)B12πf(2πfL+R)C1πf(2πfL−R)D1πf(2πfL+R)
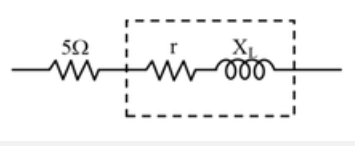
The current through an inductor of impedance 10Ω lags behind the voltage by a phase of 60∘ when just the inductor is connected to the ac source. Now the inductor is connected to a 5Ω resistance in series, then the net impedance of the circuit is
View SolutionIn a circuit L,C and R are connected in series with an alternating voltage source of frequency f. The current lead the voltages by 45∘. The value of C is :
View SolutionIn a circuit L,C and R are connected in series with an altematng voltage source of frequency f. The current leads the voltage by 60degree. The value of (Xc−XL) is
View SolutionSeries LCR circuit is connected to an AC source of angular frequency ω. Current flowing in the circuit is found to lead the voltage by π/4. Magnitude of capacitance is
View SolutionA series L-C-R circuit with a resistance of 500Ω is connected to an a.c. source of 250 V. When only the capacitance is removed, the current lags behind the voltage by 60∘. When only the inductance is removed, the current leads the voltage by 60∘. What is the impedance of the circuit?
View Solution
