A particle of charge +q and mass m moving under the influence of a uniform electric field Eˆi and a magnetic field Bˆk enters in I quadrant of a coordinate system at a point (0,a) with initial velocity vˆi and leaves the quadrant at a point
(2a.,0) with velocity −2vˆj Find
(aq) Magnitude of electric field at point (0,a) (C ) Rate of work done by both the fields at (2a,0) .
The correct Answer is:(a)3mv24qa,(b)3mv34a,(c)zero
To solve the problem, we will break it down into two parts as requested:
Part (a): Magnitude of Electric Field at Point (0, a)
1. Identify Initial and Final Conditions:
- The particle enters the first quadrant at point (0, a) with initial velocity →vi=v^i.
- The particle leaves the quadrant at point (2a, 0) with final velocity →vf=−2v^j.
2. Apply Work-Energy Theorem:
- The work done by the electric field is equal to the change in kinetic energy of the particle.
- The kinetic energy at the initial point is:
KEi=12mv2
- The kinetic energy at the final point is:
KEf=12m(−2v)2=12m(4v2)=2mv2
- The change in kinetic energy (ΔKE) is:
ΔKE=KEf−KEi=2mv2−12mv2=4mv2−mv22=3mv22
3. Relate Work Done to Electric Field:
- The work done by the electric field W can be expressed as:
W=qE⋅d
- Here, d is the distance moved in the direction of the electric field. The particle moves from (0, a) to (2a, 0), which is a distance of √(2a−0)2+(0−a)2=√4a2+a2=√5a2=a√5.
4. Set up the equation:
- Equating the work done to the change in kinetic energy:
qE⋅a√5=3mv22
5. Solve for Electric Field E:
- Rearranging gives:
E=3mv22qa√5
Part (b): Rate of Work Done by Both Fields at (2a, 0)
1. Calculate the Electric Force:
- The electric force →Fe on the particle is given by:
→Fe=qE^i
2. Calculate the Magnetic Force:
- The magnetic force →Fm is given by:
→Fm=q(→v×→B)
- At point (2a, 0), the velocity →v=−2v^j and →B=B^k:
→Fm=q(−2v^j×B^k)=−2qvB(^j×^k)=−2qvB(−^i)=2qvB^i
3. Total Force:
- The total force →F acting on the particle is:
→F=→Fe+→Fm=qE^i+2qvB^i=q(E+2vB)^i
4. Rate of Work Done:
- The rate of work done P by the electric and magnetic fields is given by:
P=→F⋅→v=q(E+2vB)(−2v^j)⋅^i=0
- Since the electric and magnetic forces are perpendicular to the velocity, the rate of work done is zero.
Final Answers:
- (a) Magnitude of Electric Field at point (0, a):
E=3mv22qa√5
- (b) Rate of work done by both fields at (2a, 0):
P=0
- The particle enters the first quadrant at point (0, a) with initial velocity →vi=v^i.
- The particle leaves the quadrant at point (2a, 0) with final velocity →vf=−2v^j.
- The work done by the electric field is equal to the change in kinetic energy of the particle.
- The kinetic energy at the initial point is:
KEi=12mv2
- The kinetic energy at the final point is:
KEf=12m(−2v)2=12m(4v2)=2mv2
- The change in kinetic energy (ΔKE) is:
ΔKE=KEf−KEi=2mv2−12mv2=4mv2−mv22=3mv22
- The work done by the electric field W can be expressed as:
W=qE⋅d
- Here, d is the distance moved in the direction of the electric field. The particle moves from (0, a) to (2a, 0), which is a distance of √(2a−0)2+(0−a)2=√4a2+a2=√5a2=a√5.
- Equating the work done to the change in kinetic energy:
qE⋅a√5=3mv22
- Rearranging gives:
E=3mv22qa√5
- The electric force →Fe on the particle is given by:
→Fe=qE^i
- The magnetic force →Fm is given by:
→Fm=q(→v×→B)
- At point (2a, 0), the velocity →v=−2v^j and →B=B^k:
→Fm=q(−2v^j×B^k)=−2qvB(^j×^k)=−2qvB(−^i)=2qvB^i
- The total force →F acting on the particle is:
→F=→Fe+→Fm=qE^i+2qvB^i=q(E+2vB)^i
- The rate of work done P by the electric and magnetic fields is given by:
P=→F⋅→v=q(E+2vB)(−2v^j)⋅^i=0
- Since the electric and magnetic forces are perpendicular to the velocity, the rate of work done is zero.
- (a) Magnitude of Electric Field at point (0, a):
E=3mv22qa√5
- (b) Rate of work done by both fields at (2a, 0):
P=0
Similar Questions
A particle of charge +q and mass m moving under the influence of as uniform electric field Eˆi and uniform magnetic field Bˆk follows trajectory form P to Q as shown in figure. The velocities at P and Q re vˆiand−2ˆj. Which of the following statement(s) is/are correct?
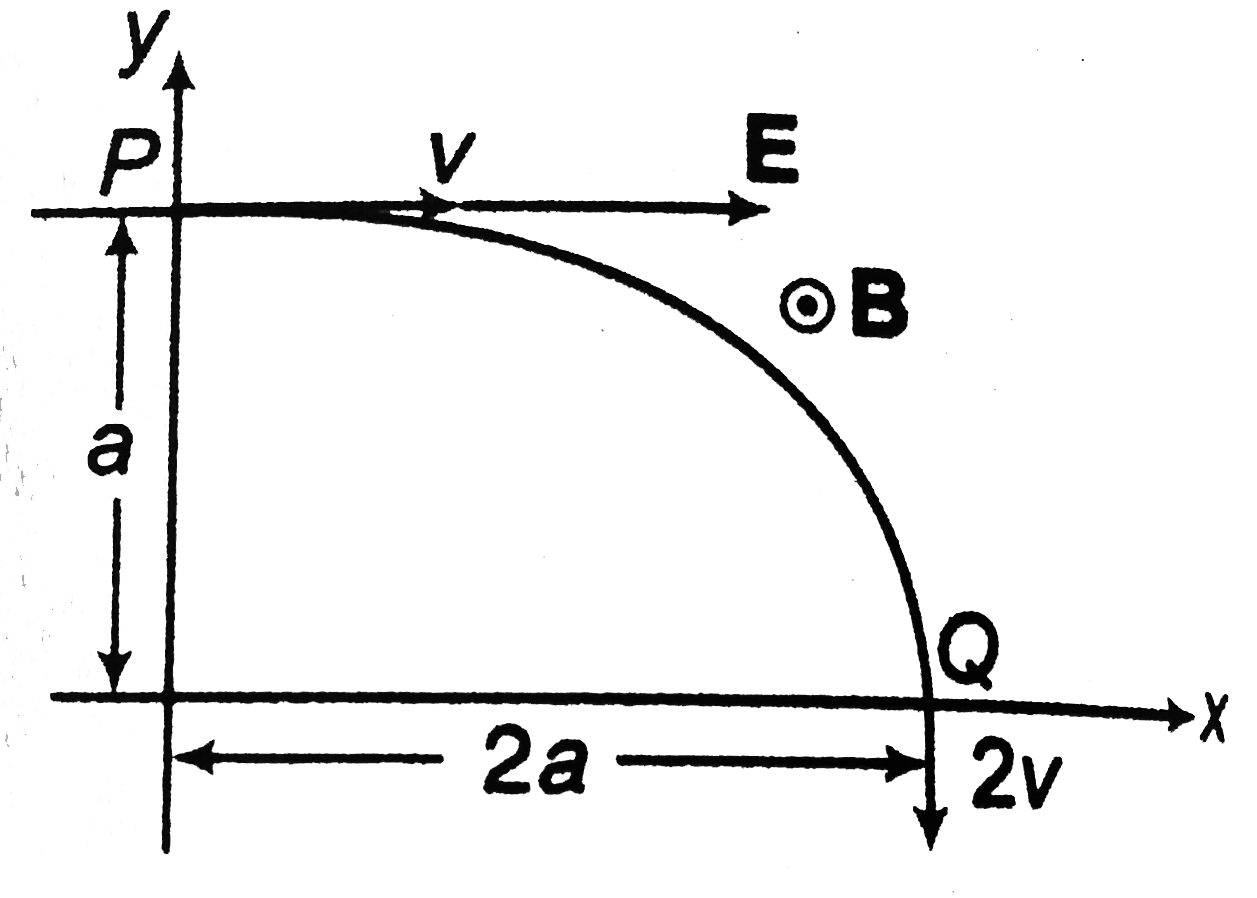
a.E=34[mv2qa]
b. Rate of work done by the electrif field at P is 34[mv3a]
c. Rate of work done by the electric field at P is zero.
d. Rate of work done by both the field at Q is zero.
View SolutionA particle of charge q and mass m starts moving from the origin under the action of an electric field →E=E0ˆi and →B=B0ˆi with velocity →v=v0ˆj. The speed of the particle will become 2v0 after a time
View Solution
Knowledge Check
A particle of charge +q and mass m moving under the influnce of a uniform electric field Eˆiand a uniform magnetic field Bˆk follows trajectory from P to Q as shown in figure. The velocities at P and Q vˆi and −2vˆj respectively. Which of the following statement(s) is/are correct
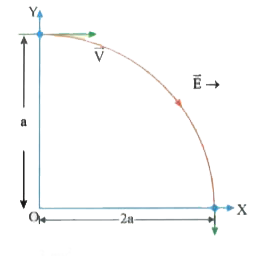 AE=34mv2qaBRate of work done by electric field at Pis 34mv3aCRate of work done by electric field at P is zeroDRate of work done by both the fields at Q is zero
AE=34mv2qaBRate of work done by electric field at Pis 34mv3aCRate of work done by electric field at P is zeroDRate of work done by both the fields at Q is zeroA particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of is
A25mv20qE0B100mv20qB0C50mv20qE0D14mv20qE0A particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of is
A25mv20qE0B100mv20qB0C50mV20qE0D14mv20qE0
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
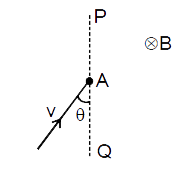
time spent
View SolutionA particle of charge q=4μC and mass m = 10 mg starts moving from the origin under the action of an electric field →E=4ˆi and magnetic field →B=(0.2T)ˆk. Its velocity at (x, 3, 0) is (4→i+3→j). The value of x is -
View SolutionA charged particle moving with velocity vis subjected to electric field E and magnetic field B. The particle will go undeflected if
View SolutionA proton (or charged particle) moving with velocity v is acted upon by electric field E and magnetic field B. The proton will move undeflected if
View SolutionA particle of charge q and mass m starts moving from the origin under the action of an electric field →E=E0ˆiand→B=B0ˆi with a velocity →v=v0ˆj. The speed of the particle will become 2v0 after a time.
View Solution
