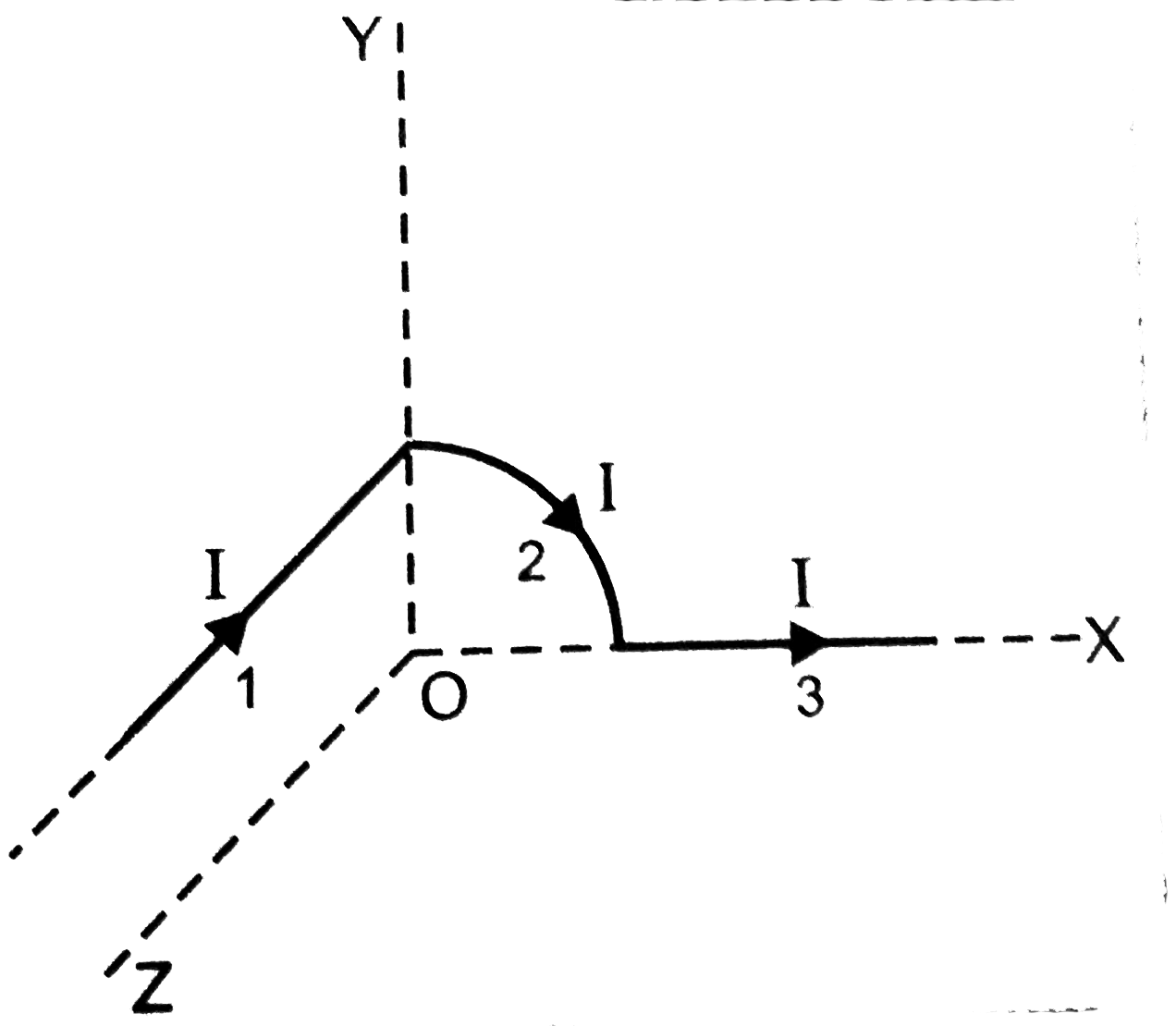
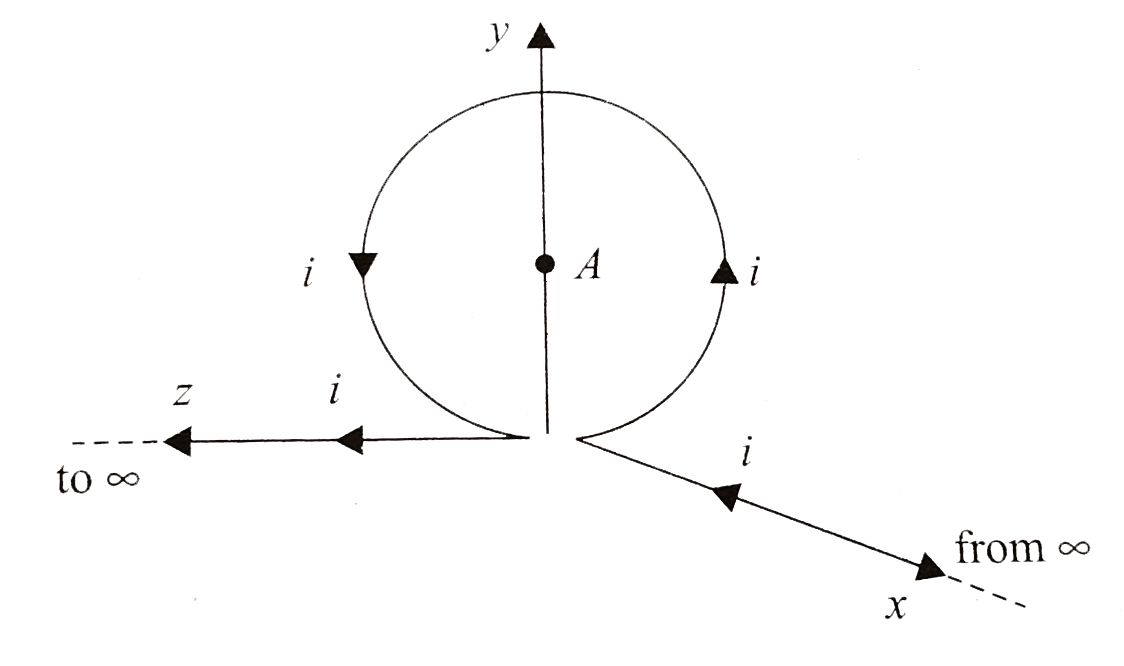
Find the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors along which a current I is flowing at a point A (O, R, O), that is the centre of a circular conductor of radius R. The ring is in yz plane.
Video Solution
Text Solution
The correct Answer is:B=μ0i4πR√2(2π2−2π+1)
→B1=μ04πIR(−ˆk)→B2=μ04π2πIR(ˆi)
−→B3=μ04πIR(−ˆi)
→B=→B1=→B2→B3
=μ04πIR(2π−1)ˆi+μ04πIR(ˆk)
B=μ04πIR√(2π−1)2+1
=μ04πIR√2(2π2−2π+1)
 .
.
|
Similar Questions
Knowledge Check
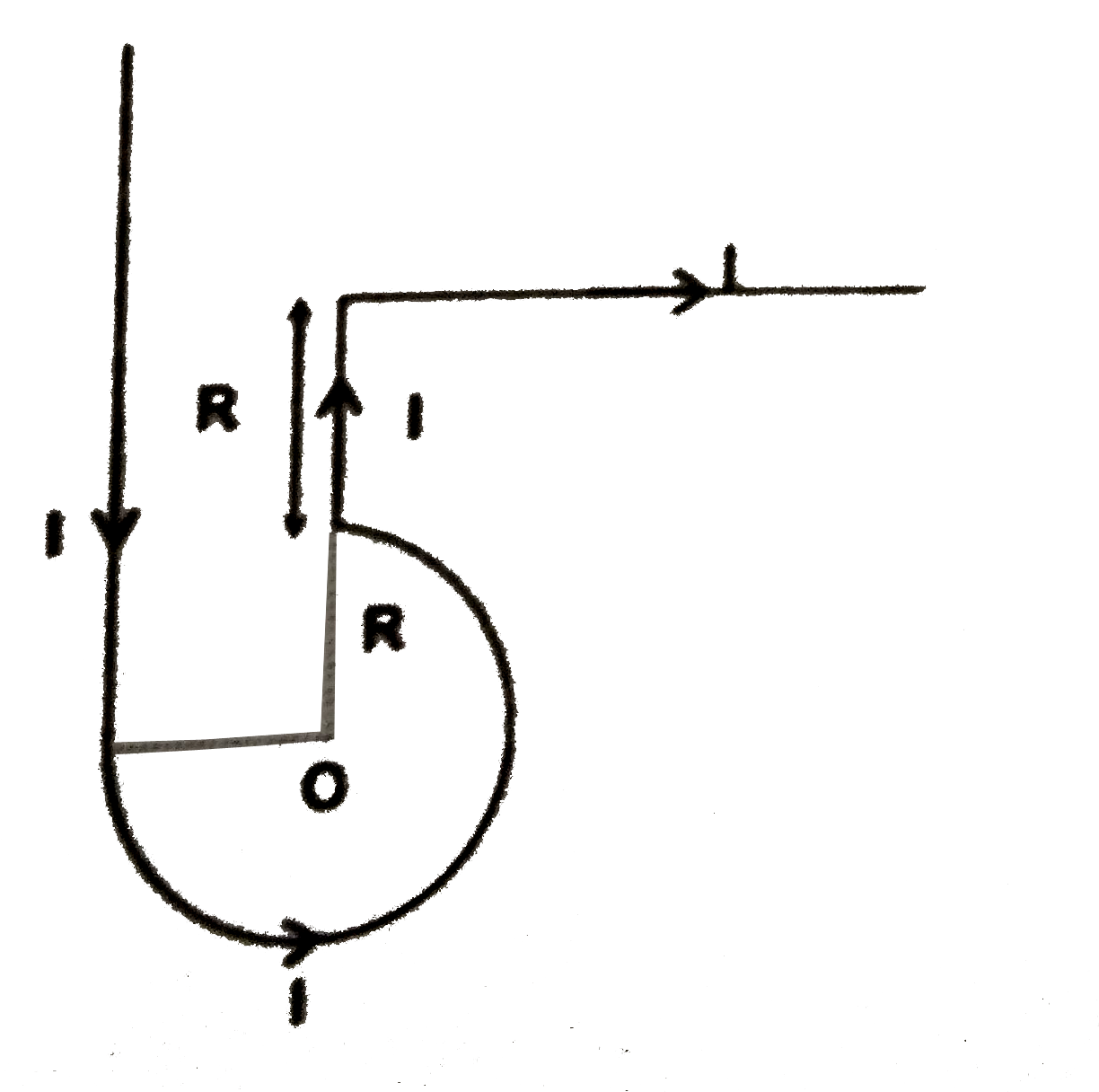
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)Magnetic field at some point, generated by a current bearing conductor, is proportional to
Aresistance of the conductorBthickness of the conductorCcurrent passing through conductorDdistance from the conductorThe magnetic induction at O due to a current in conductor shaped as shown in figure
 Aμ0i4π[3π2a+√2b]Bμ0i4π[3π4a−√2b]Cμ0i4π[3π4a+1√2b]Dμ0i4π[1a+1b]
Aμ0i4π[3π2a+√2b]Bμ0i4π[3π4a−√2b]Cμ0i4π[3π4a+1√2b]Dμ0i4π[1a+1b]
Find the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionThe magnetic induction at the centre of a current carrying circular of coil radius r, is
View SolutionA cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
View SolutionA long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
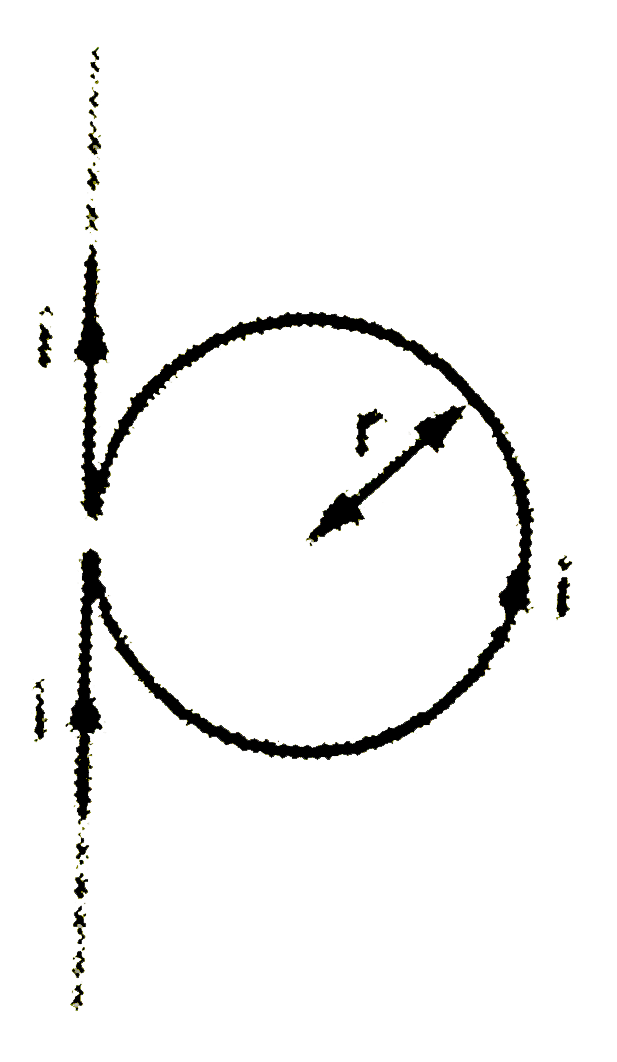
View Solution