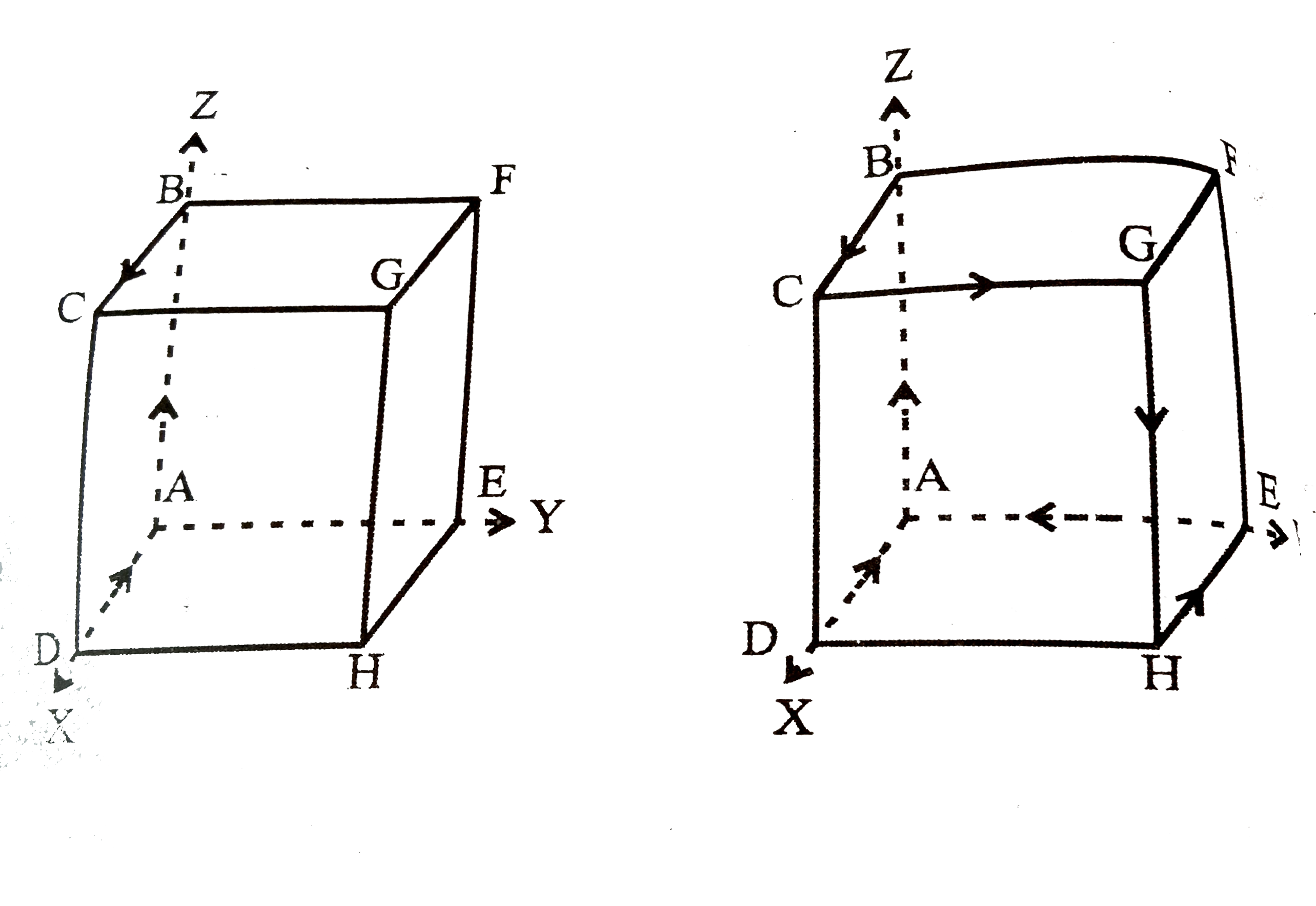
Current I si following along the path ABCD, along the four edges of the cube (figure-a) creates a magnetic field in the centre at the center of the cube current I flowing along the path of the six edges ABCDHEA .
√32B0 Towards corner G .
√3B0 Towards corner E
√32B0 Towards conrner H .
√3B0 Towards corner F .
The correct Answer is:D
Each edge share current for two loops so cur rent for one loop is 12 and its field at centre of loop is B02 There are sin loops
→B=(B02+B02)ˆk
→B=B0ˆi+B0ˆj+B0^ˆk
B=√3B0 towards F .
Similar Questions
Knowledge Check
Along the direction of current carrying wire, the value of magnetic field is ?
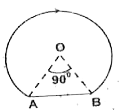
AzeroBinfinityCdepends on the length the wireDuncertainA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
 Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)A square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
Aμ0l2√2πaB2√2μ0lπaCμ0l√2πaDμ0l√2πa
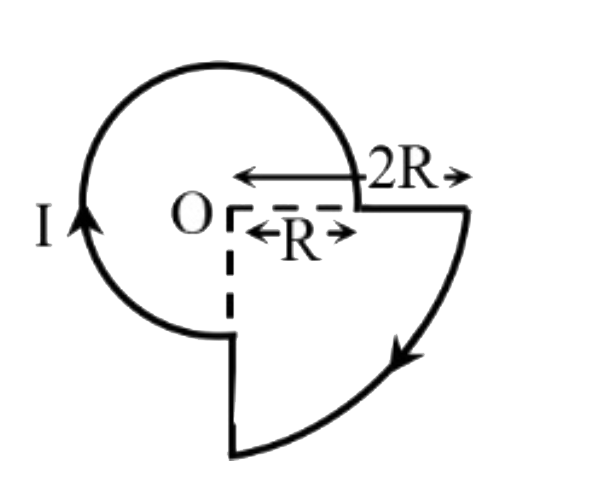
A current I flows along a thin-walled, long, half-cylinder of radius R(figure) Find the magnetic induction at a point on the axis of the cylinder
View SolutionA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
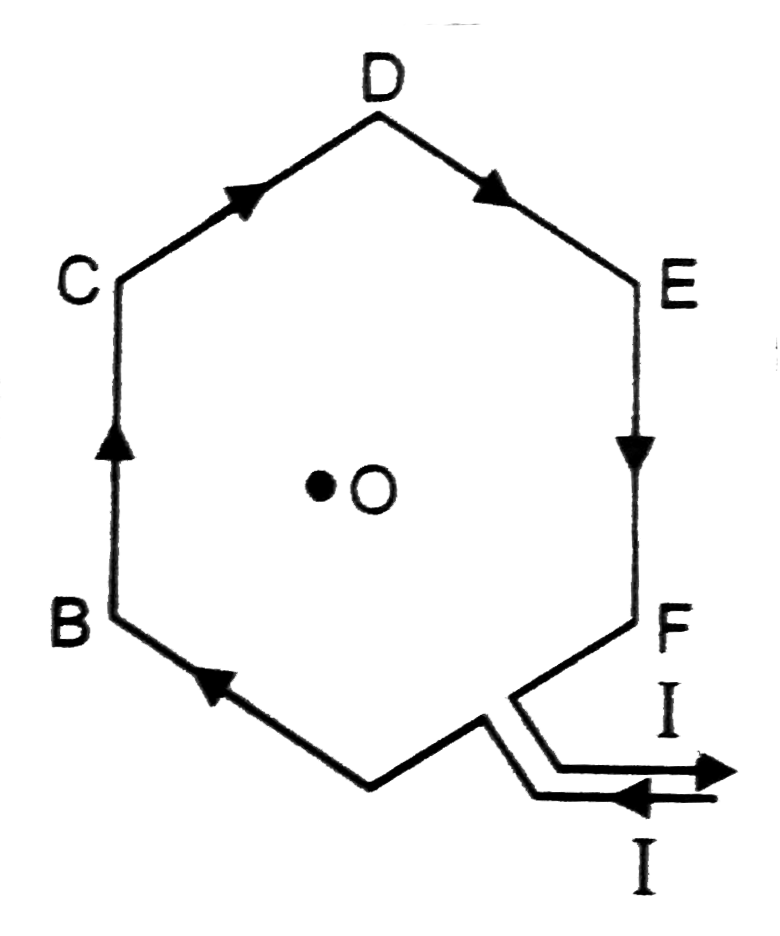
View SolutionThe current is flowing along the path abcd of a cube (shown to the left) produces a magnetic field at the centre of cube of magnitude B. Dashed line depicts the non-conducting part of the cube.

Consider a cubical shape shown to the right which is identical in size and shape to the left. If the same current now flows in along the path daefgcd, then the magnitude of magnetic field at the centre will be
View SolutionA current 1 flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
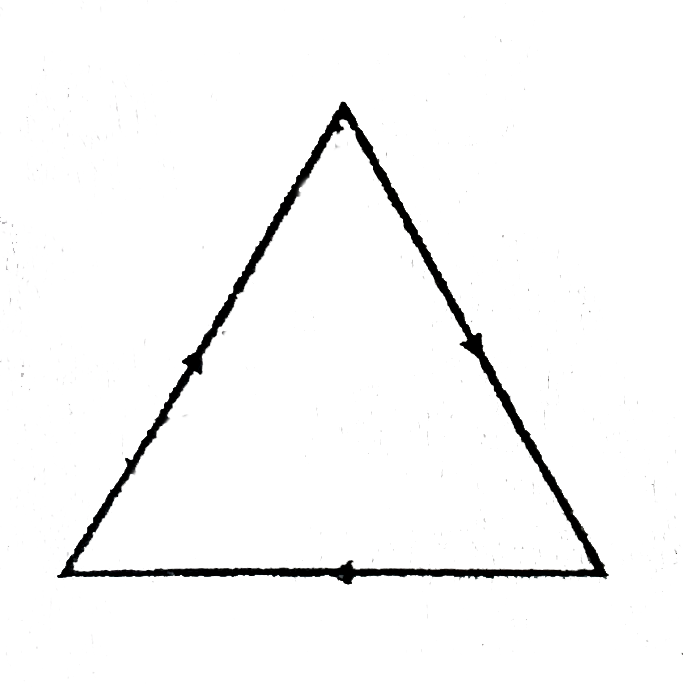
View SolutionA current 1 flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
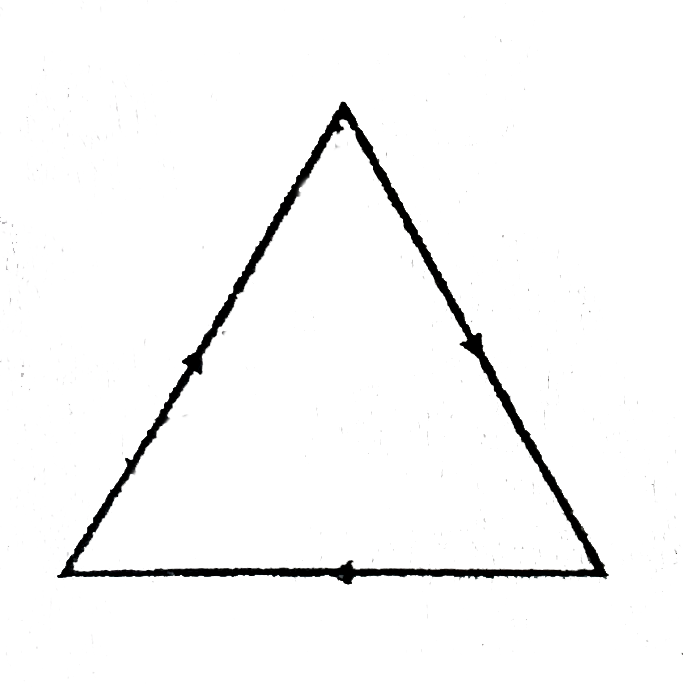
View Solution