The ratio of power dissipated respectively in R and 3R, as shown is:

9
27/4
4/9
4/27
The correct Answer is:D
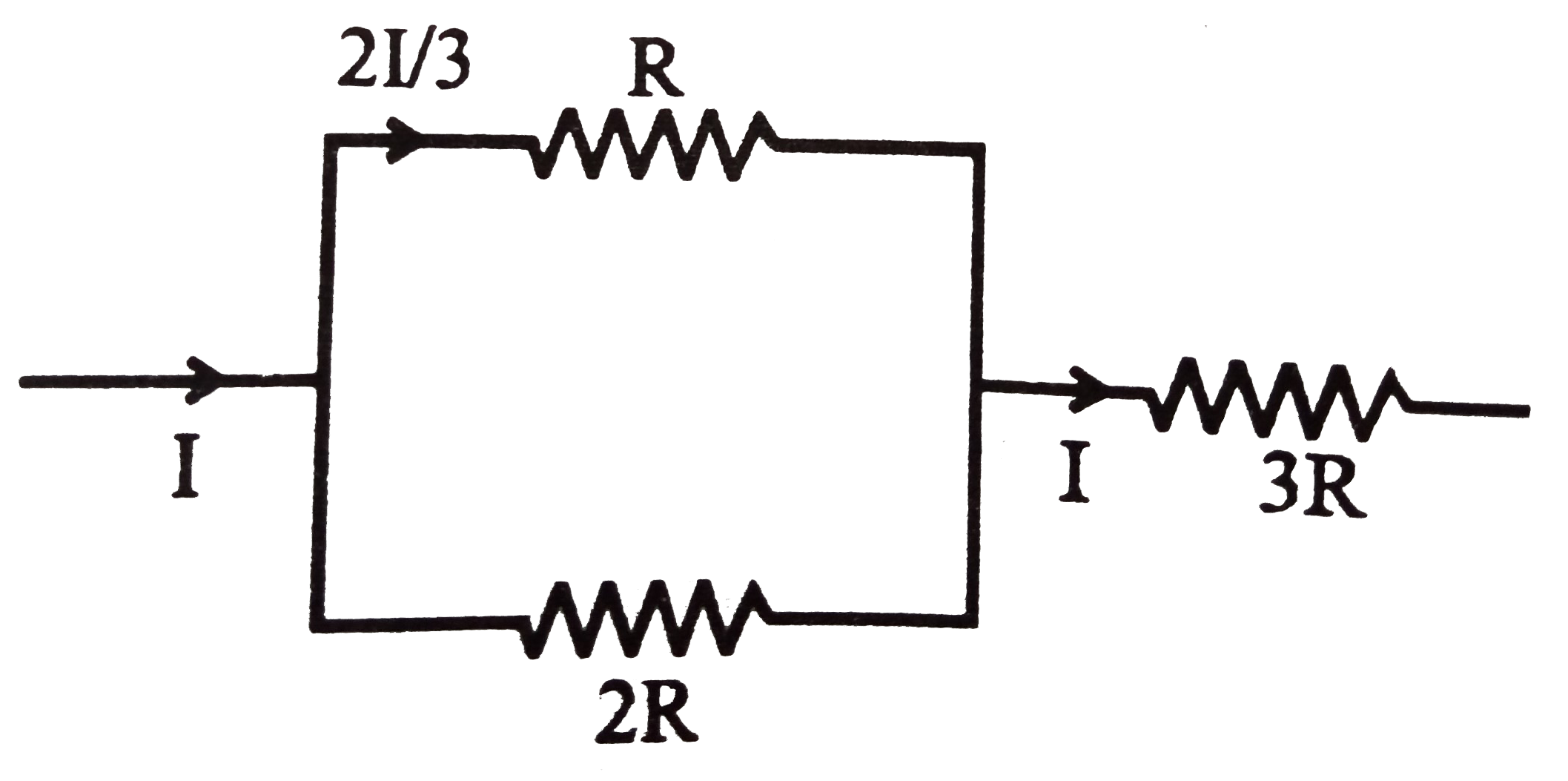
IR=2R3R×I=2I3&H=I2R
HRH3R=(IRI3R)2×R3R=(23)2×13=427
Similar Questions
The ratio of powers disspatted respectively in R and 3R , as shown is
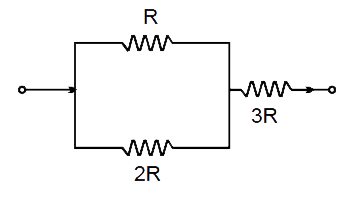
View Solution(a) Two heater coils made of the same material are connected in paralled across the mains. The length of diameter of one the coil is triple that of other. Which of these will produce more heat?
(b) Three equal resistors connected in series across a source of emf together dissipated 10Wa of power. What would be the power disspated if the same resistors are connected in parallel across the same source of emf?
Two resistor R1 and R2 may be connect either in series or in parellel across a battery of zero internal resistance. it is required that joule heating for the parallel combination be four times than for series combination. if R1=100Ω find R2
(d) The three resistance A,BandC have values 3R,6R and R respectively. Now some potential difference is applied across the network . Find the ratio of thermal powers dissipated between X and Y . find ratio of power consumed by A,B,andC.
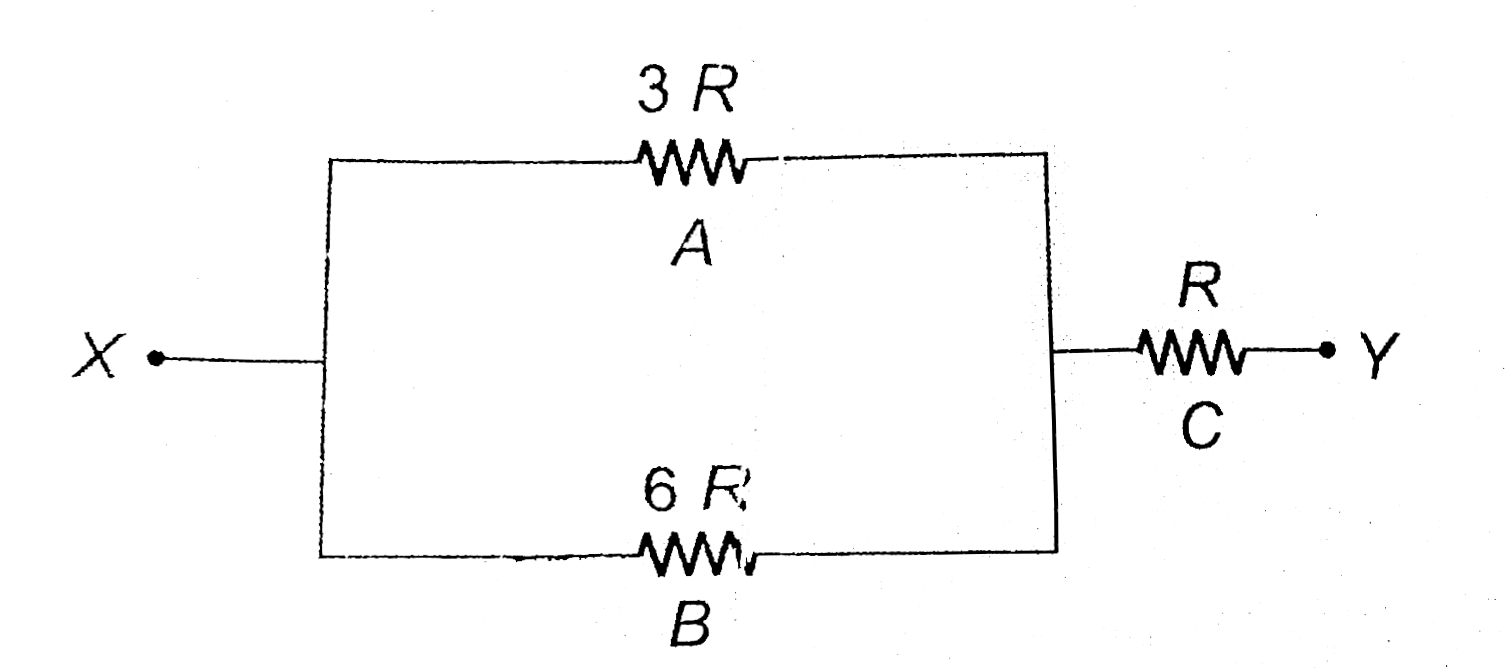
View Solution
Knowledge Check
The power dissipated in 3Ω resistor in the circuits as shown in the figure is 2W. The power dissipated in 7Ω resistor will be
 A14WB143WC73WD7W
A14WB143WC73WD7WA galvanometer of resistance RG is to be converted into an ammeter, with the help of a shunt of resistance R. If the ratio of the heat dissipated through galvanometer and shunt is 3:4, then
AR=34RGB43RG=RC9R16=RGD16R9=RGThe total power dissipated in watts in the circuit shown here is
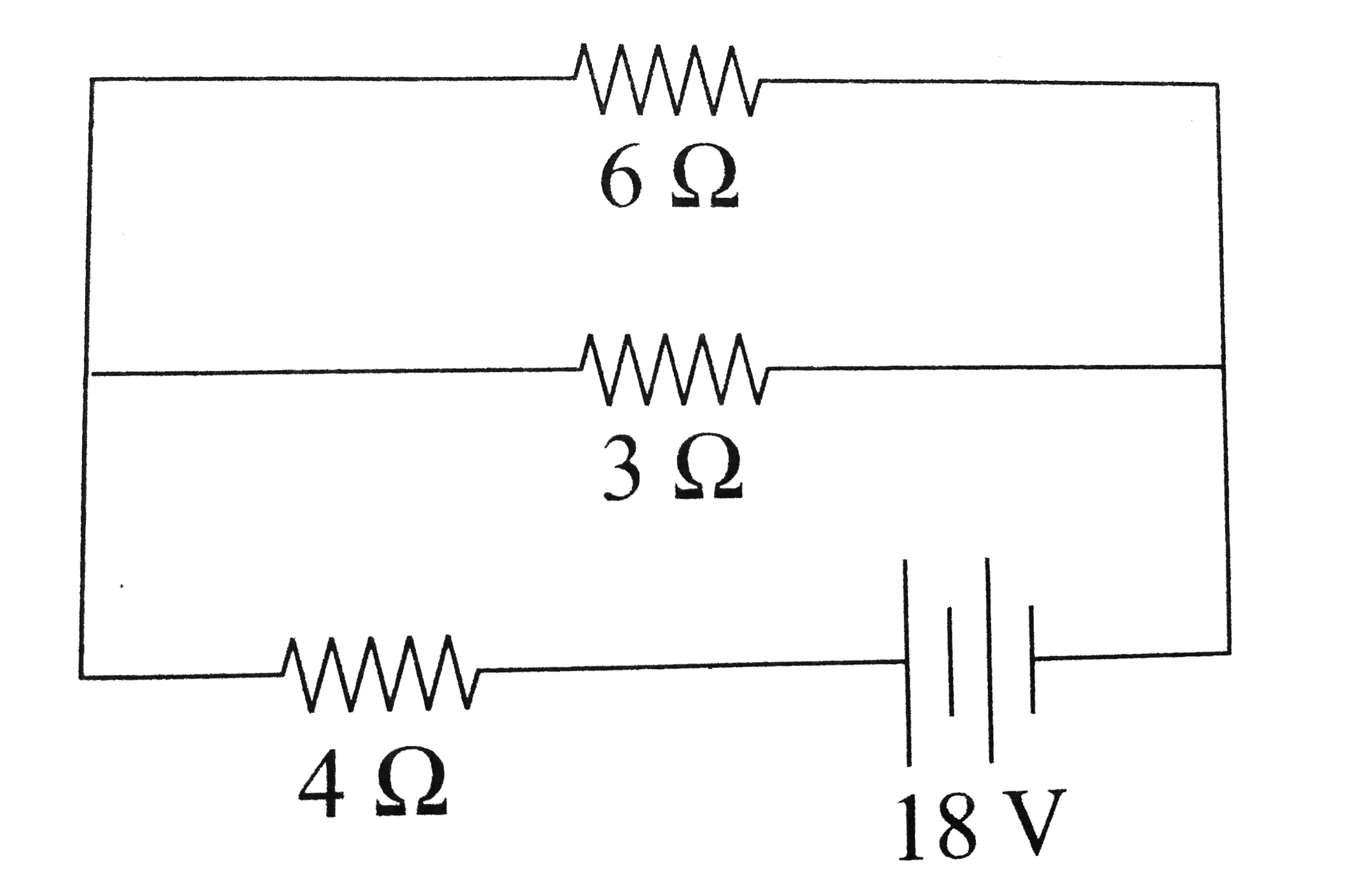 A16B40C54D4
A16B40C54D4
Figure shows the net power dissipated in R versus the current in a simple circuit shown.
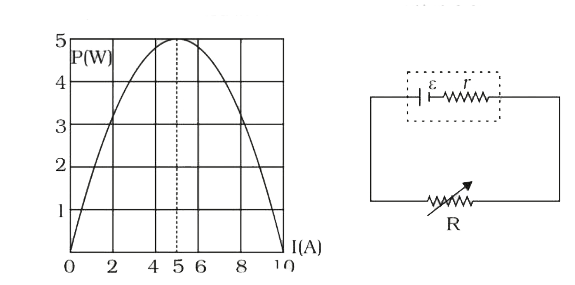
View SolutionThe maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
View SolutionThe maximum power dissipated by external resistance R by a cell of an external omf E and internal resistance r is E2/4R which is obtained for
View SolutionTwo resistors R1andR2 of 4Ωand6Ω are connected in parallel across a battery. The ratio of power dissipated in them, P1:P2 will be:
View SolutionThe power dissipated in resistor R is 16R wat, whether the switch S is closed or open. The unknown e.m.f ε in the circuit is
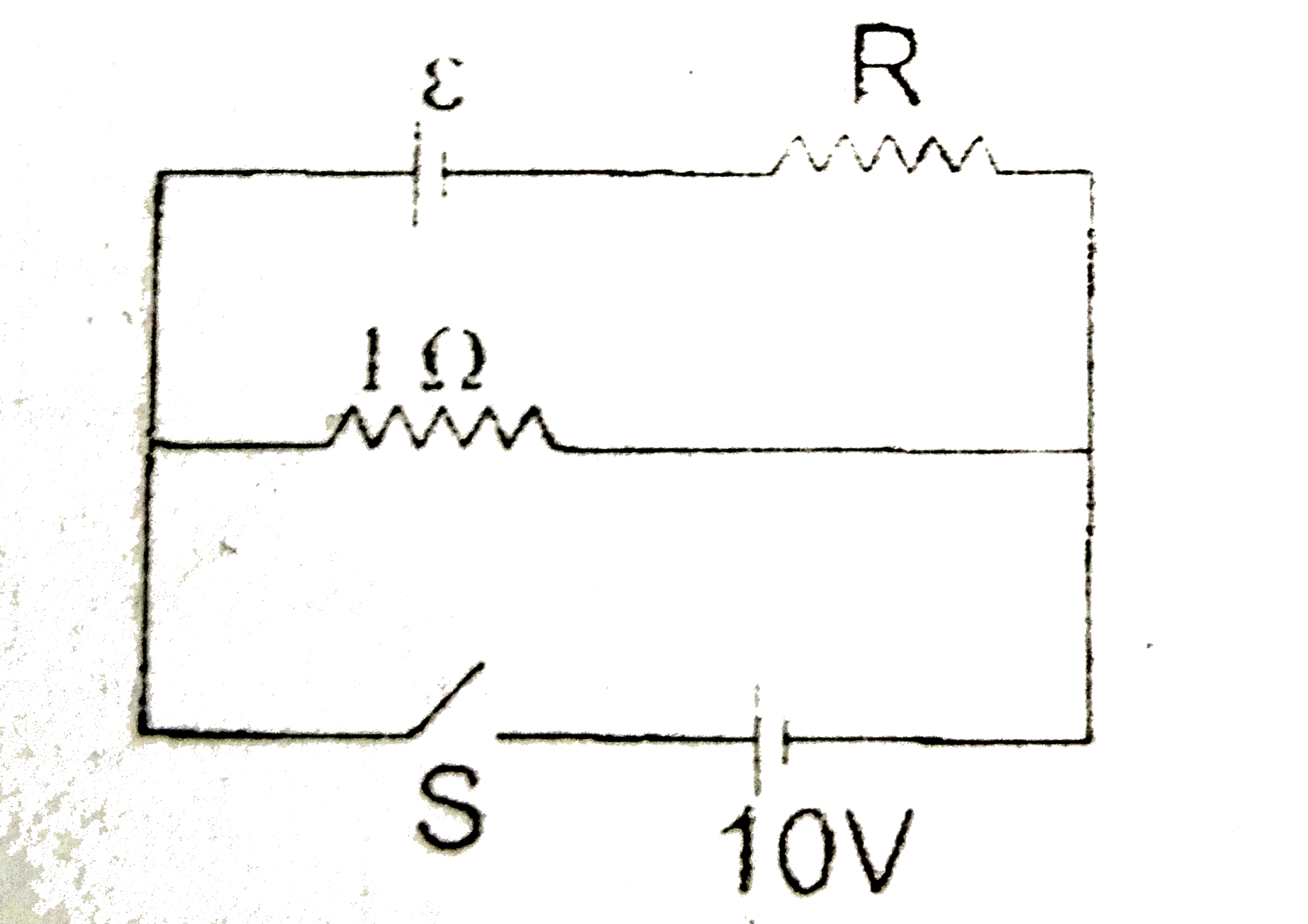
View Solution