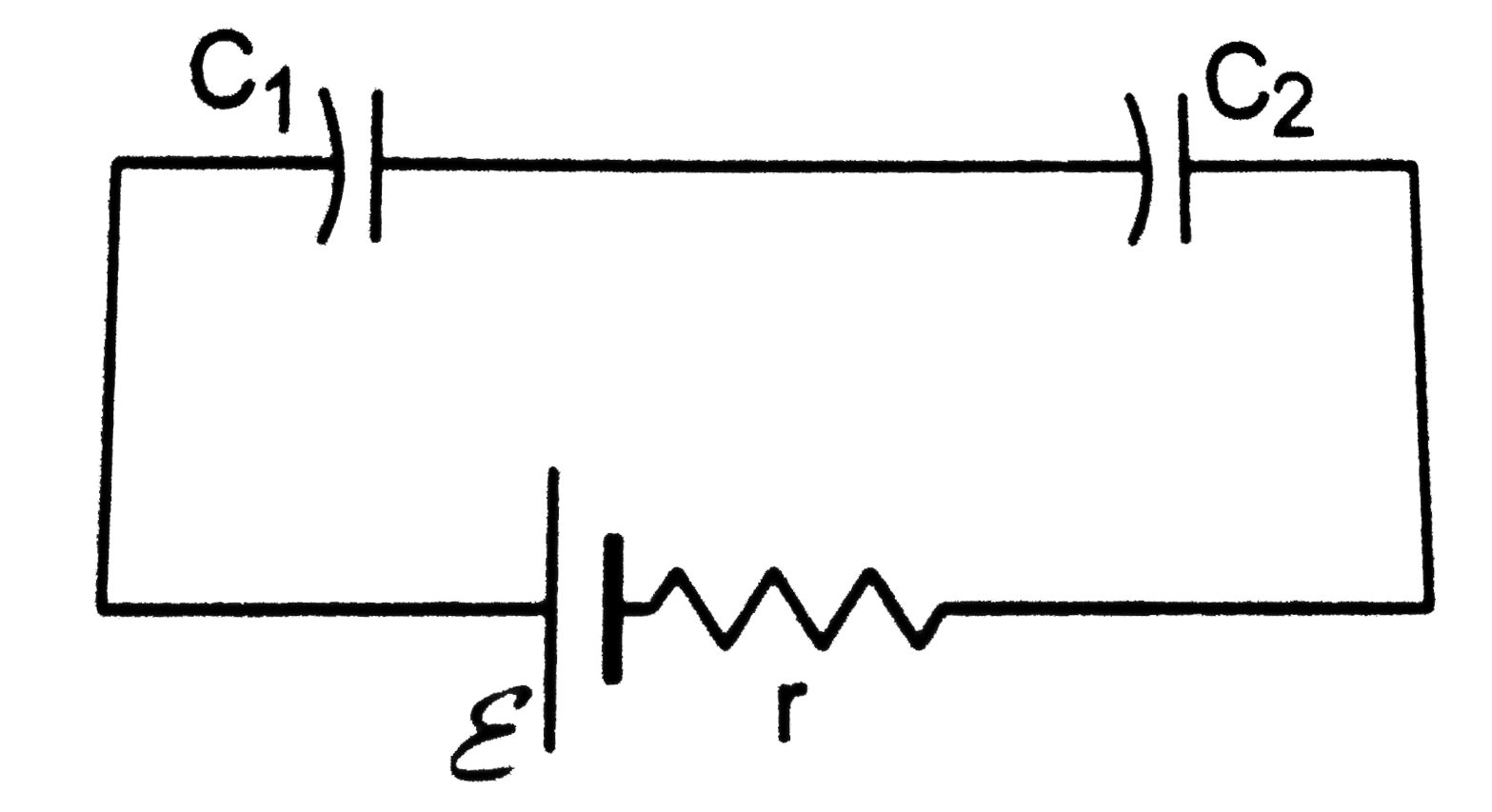
Initially the switch is open for a long time. Now the switch is closed at t=0. Find the charge on the rightmost capacitor as a function of time given that it was initially uncharged.
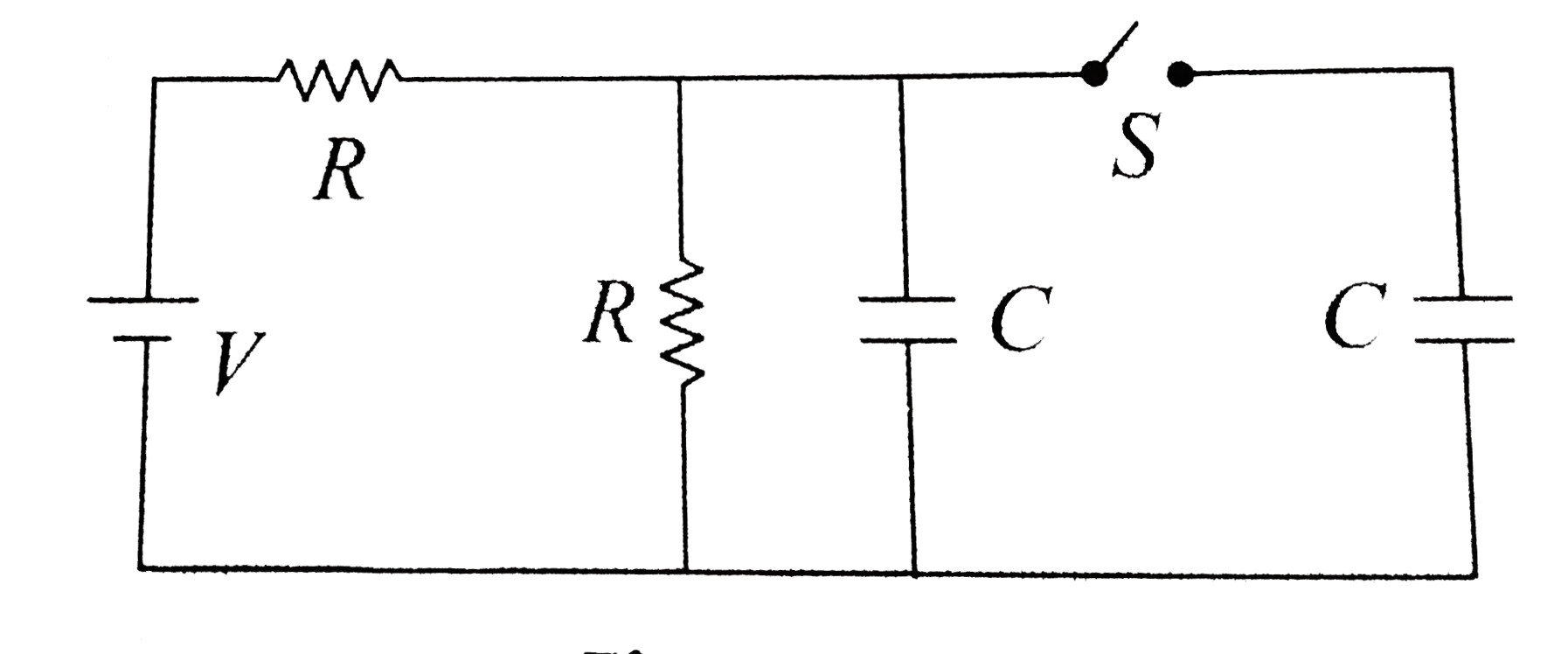
The correct Answer is:q=CV2(1−12e−t/RC
Before closing the switch charge distribution will be-
VAB=V2R'R=V2

Let switch in closed at t=0 and charge on
right capacitors is q(q1=CV4 between each capacitor) So charge on capacitor
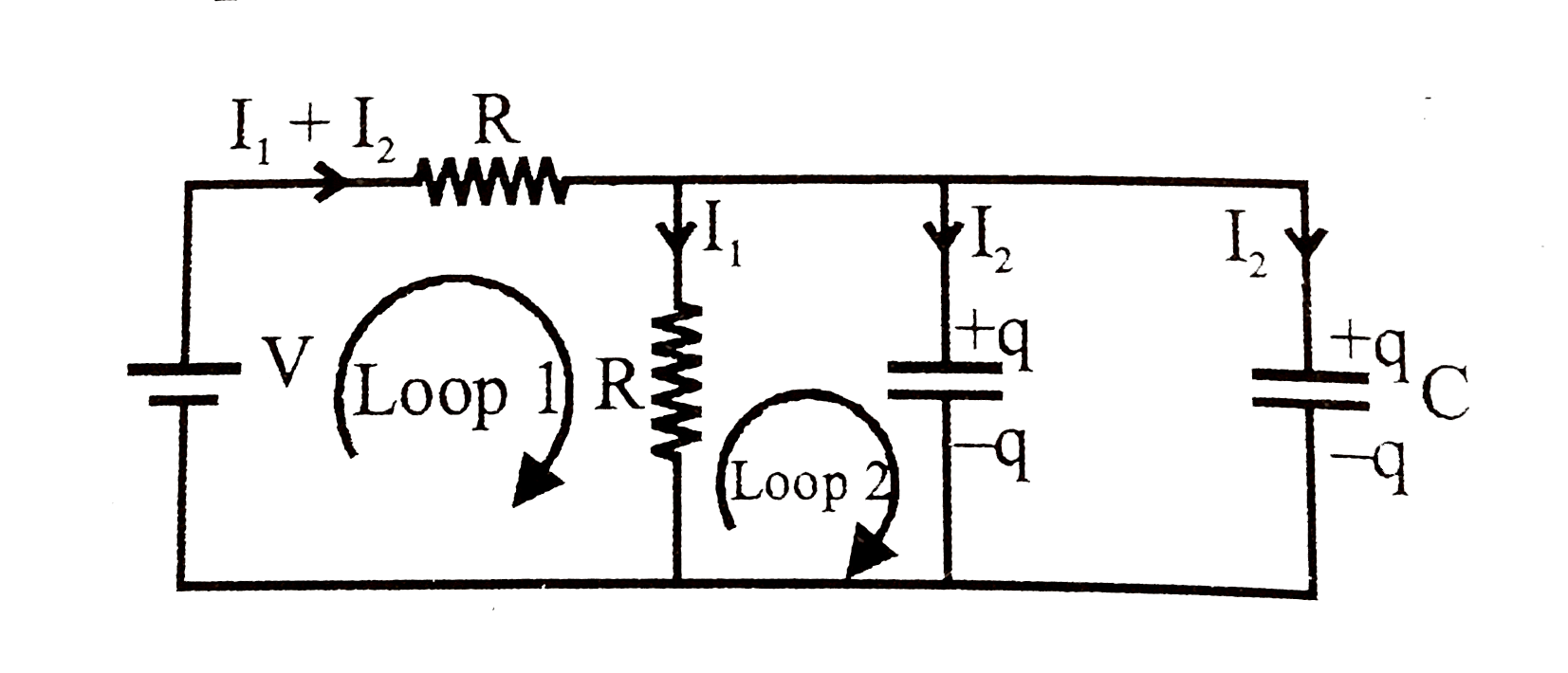
For loop (1)
V−(l1+2l2)R−l1R=0
2l2R=V−2l1R....(1)
For loop (2)
l_(1) R - (q)/(C ) = 0 Þ l_(1) R = (q)/(C )...(2)
From (1) and (2)
2l2R=V−2qC...(3)
we have l2=dqdt..(4)
From (3) and (4)
2Rdqdt=CV−2qC
overset(q)underset(q_(l)=CV//4)Ò(dq)/(CV-2q)=overset(t)underset(0)Ò(dt)/(2RC)
overset(é)(ê)"ln"(CV_2q)/(-2)overset(ù^(q))(ú)_(CV//4) (t)/(2RC)
CV−2qCV−CV/2=e−t/RC
CV−2q=CV2e−t/RC
2q=CVoverset(æ)underset(è)(C1)-(1)/(2)e^(t//RC)overset(Ö)underset(Ø)(./div)
q=CV2æC1è−12et/RCÖ.÷Ø
An soon as switch is closed at the same momnet charge sharen between two capaitor which is initial charge on each capacitor.

τ=R2×2C=RC
Time varying charge on capacitor
q=V2×2C(1−e−t/RC))+2q0e−t/RC=CV(1−e−t/RC+CV2e−t/RC
q=(CV)(1−12e−t/RC)
time verying charge on each capacitor =
q2=CV2(1−12e−t/RC)
Similar Questions
initially the switch is open for a long time. Now the swithc is closed at t=0. find the caharge on the rightomost capacitor as a function of time given that it was initially unchanged.

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View Solution
Knowledge Check
The switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
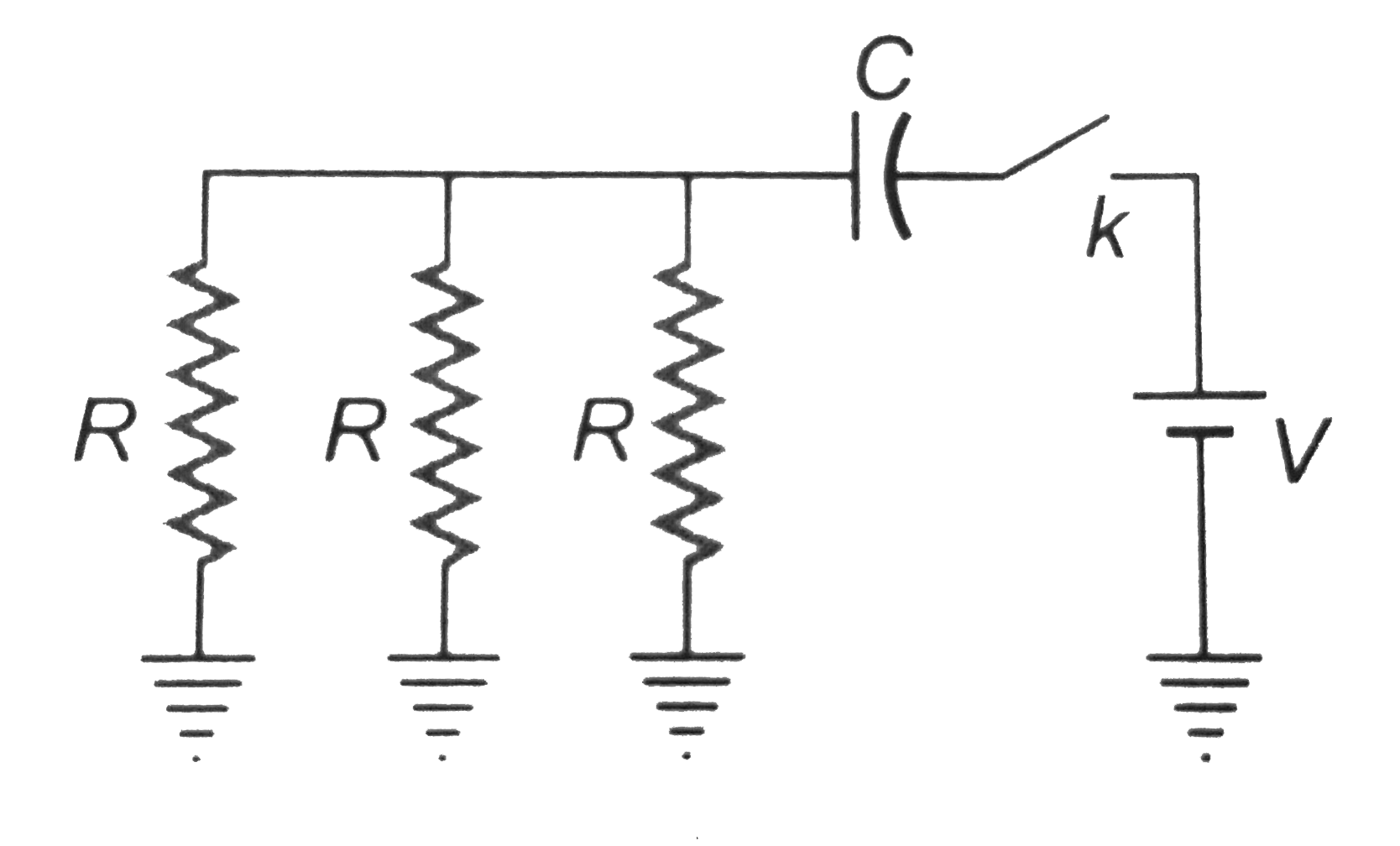 ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC)
ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC)In precious question the switch is kept closed for a long time and then assume it is opened at t = 0. Write the expression of charge on the capacitor as a function of time.
Aq=2CVe−t/3RCBq=CVe−t/3RCCq=CVe−t/2RCDq=CVe−2t/3RCThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
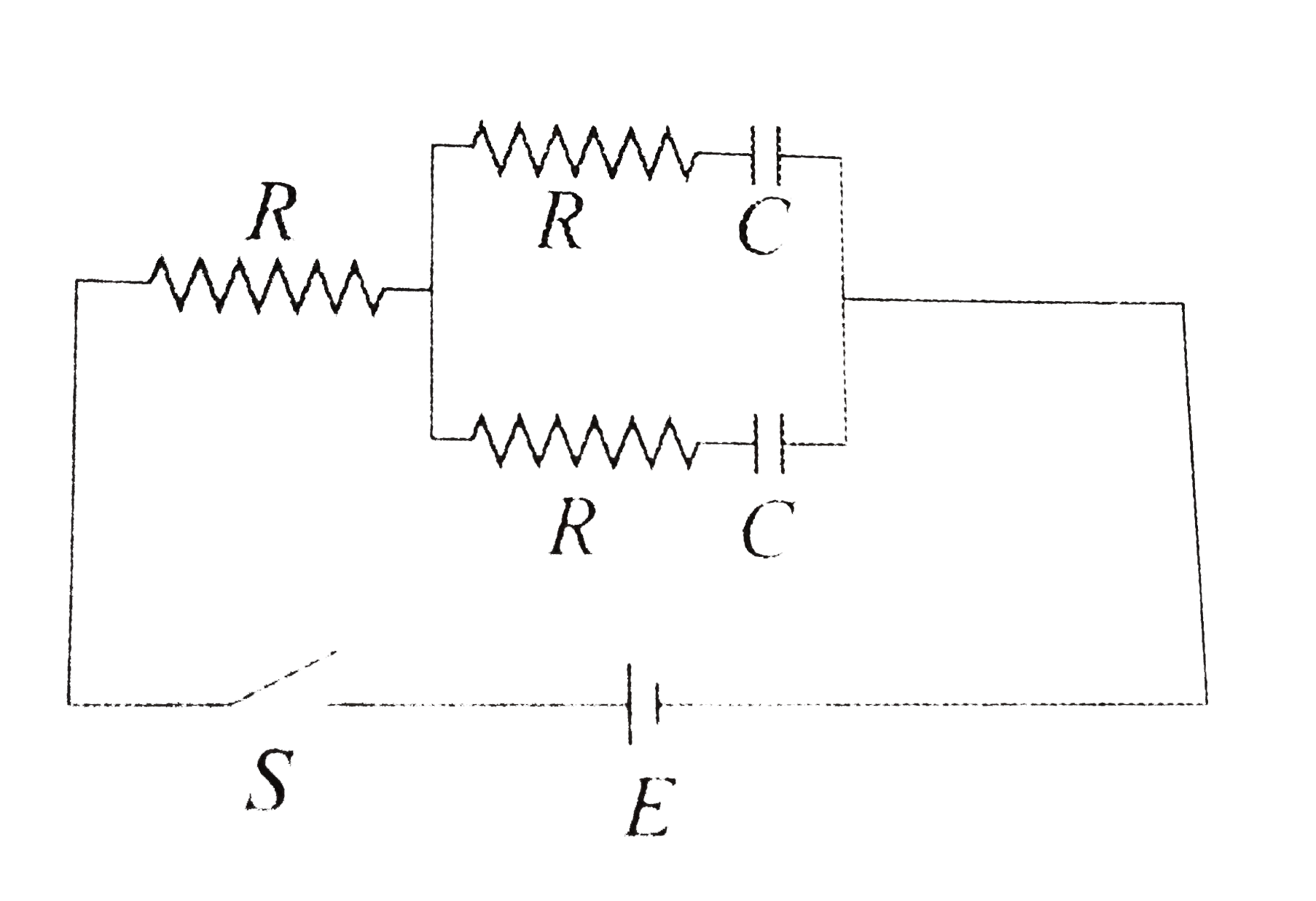 Aqt=EC(1−e−2t/3RC)Bqt=EC(1−e−t/2RC)Cqt=EC(1−e−t/3RC)Dqt=EC(1−e−3t/2RC)
Aqt=EC(1−e−2t/3RC)Bqt=EC(1−e−t/2RC)Cqt=EC(1−e−t/3RC)Dqt=EC(1−e−3t/2RC)
Consider the situation shown in figure.The switch is closed at t=0when the capacitor C1as a function of time t.
View SolutionIn figure-5.143 ifS is closed at t=0, find charge on capacitor as a function of time. Time inductor is active with initial current I0 in it.

View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionIn Fig. switch S is closed for a long time. At t=0, if it is opened, then

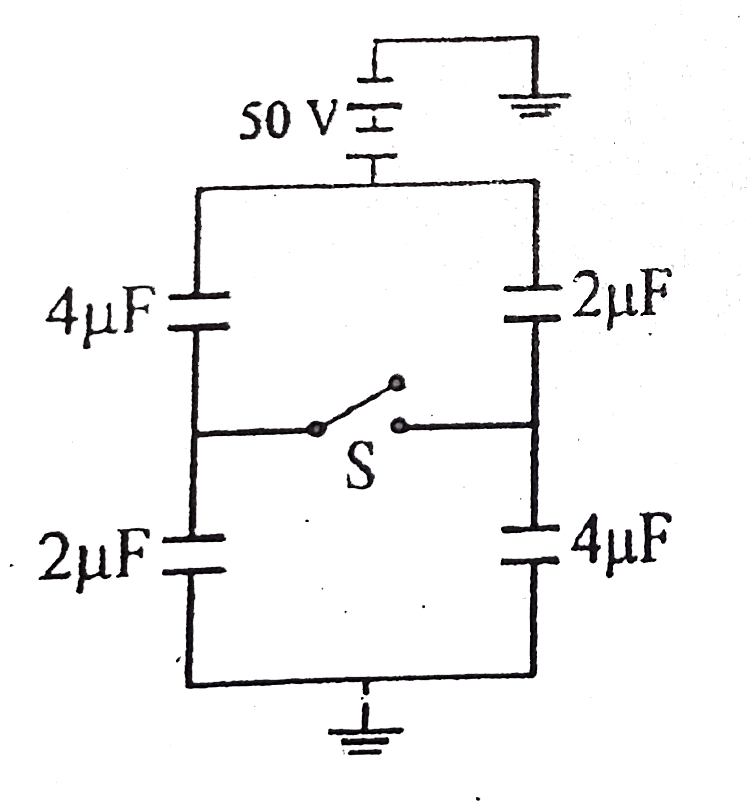
View SolutionThe circuit was in the shown state from a long time. Now the switch S is closed. The charged that flows through the switch is
View Solution