A capacitor stores 60μC charge when connected across a battery. When the gap between the plates is filled with a dielectric, a charge of 120μC flows through the battery. The dielectric constant of the material inserted is:
1
2
3
none
The correct Answer is:C
To solve the problem, we need to find the dielectric constant (K) of the material inserted between the plates of the capacitor. We start with the information given:
1. The initial charge stored in the capacitor (Q1) is 60 µC.
2. After inserting the dielectric, the new charge stored (Q2) is 180 µC (60 µC + 120 µC).
Step 1: Understand the relationship between charge, capacitance, and voltage.
The charge stored in a capacitor is given by the formula:
Q=C⋅V
Where:
- Q is the charge,
- C is the capacitance,
- V is the voltage.
Step 2: Establish the initial and final conditions.
Initially, we have:
Q1=C1⋅V
After inserting the dielectric:
Q2=C2⋅V
Where C2 is the capacitance with the dielectric.
Step 3: Relate the capacitance with and without the dielectric.
The capacitance of a capacitor with a dielectric is given by:
C2=K⋅C1
Where K is the dielectric constant.
Step 4: Substitute the capacitance relationship into the charge equations.
From the equations for charge:
Q1=C1⋅V
Q2=C2⋅V=K⋅C1⋅V
Step 5: Express the charges in terms of capacitance and voltage.
We can express Q2 as:
Q2=K⋅Q1
Step 6: Substitute the known values.
We know:
- Q1=60μC
- Q2=180μC
Substituting these values into the equation:
180μC=K⋅60μC
Step 7: Solve for the dielectric constant (K).
To find K, rearrange the equation:
K=Q2Q1=180μC60μC=3
Final Answer:
The dielectric constant of the material inserted is K=3.
---
2. After inserting the dielectric, the new charge stored (Q2) is 180 µC (60 µC + 120 µC).
The charge stored in a capacitor is given by the formula:
Q=C⋅V
Where:
- Q is the charge,
- C is the capacitance,
- V is the voltage.
Initially, we have:
Q1=C1⋅V
After inserting the dielectric:
Q2=C2⋅V
Where C2 is the capacitance with the dielectric.
The capacitance of a capacitor with a dielectric is given by:
C2=K⋅C1
Where K is the dielectric constant.
From the equations for charge:
Q1=C1⋅V
Q2=C2⋅V=K⋅C1⋅V
We can express Q2 as:
Q2=K⋅Q1
We know:
- Q1=60μC
- Q2=180μC
180μC=K⋅60μC
To find K, rearrange the equation:
K=Q2Q1=180μC60μC=3
The dielectric constant of the material inserted is K=3.
Similar Questions
A capacitor stores 50μccharge when connected across a battery . When the gap between the plates is filled with a dielectric , a charge of 100muc flows through the battery .Find the dielectric constant of the material inserted.
View SolutionA capacitor gets a charge of 60μC when it is connected to a battery of emf 12 V. Calculate the capacitance of the capacitor.
View Solution
Knowledge Check
While a capacitor remains connected to a battery and dielectric slab is applied between the plates, then
APotential difference between the plates is changedBChange flows from the battery to the capacitorCElectric field between the plates increasesDEnergy store in the capacitor decreasesA parallel plate air condenser is charged and then disconnected from the charging battery. Now the space between the plates is filled with a dielectric then, it electric field strength between the plates
Aincreases while its capacity increasesBincreases while its capacity decreasesCdecreases while its capacity increasesDdecreases while its capacity decreasesA parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
A250μCB250nCC200nCD200μC
A capacitor of some capacitance is charged by a 12V battery.Now the space between the plates of capacitors is filled with a dielectric of dielectric constant K=0.5 and again it is charged. The magnitude of the charge will
View SolutionA 6×10−4 F parallel plate air capacitor is connected to a 500 V battery. When air is replaced by another dielectric material, 7.5×10−4C charge flows into the capacitor. The value of the dielectric constant of the material is
View SolutionA parallel plate capacitor is charged completely and then disconnected from the battery. IF the separation between the plates is reduced by 50% and the space between the plates if filled with a dielectric slab of dielectric constant 10, then the potential difference between the plates
View SolutionA parallel plate condenser is charged by connected it to a battery. Without disconnected the battery, the space between the plates is completely filled with a medium of dielectric constant k. Then
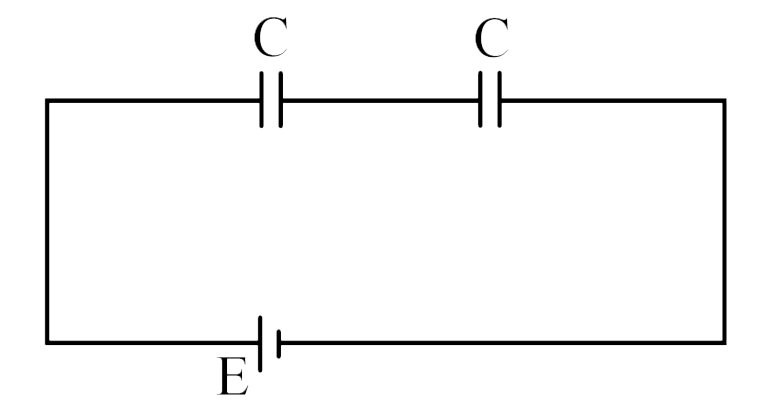
View SolutionTwo identical parallel plate capacitors of capacitance C each are connected in series with a battery of emf, E as shown. If one of the capacitors is now filled with a dielectric of dielectric constant k, the amount of charge which will flow through the battery is (neglect internal resistance of the battery)
View Solution