Let be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance from the centre of the sphere, the magnitude of electric field is:
The correct Answer is:C
Consider a spherical shell having radius and thickness dr
or
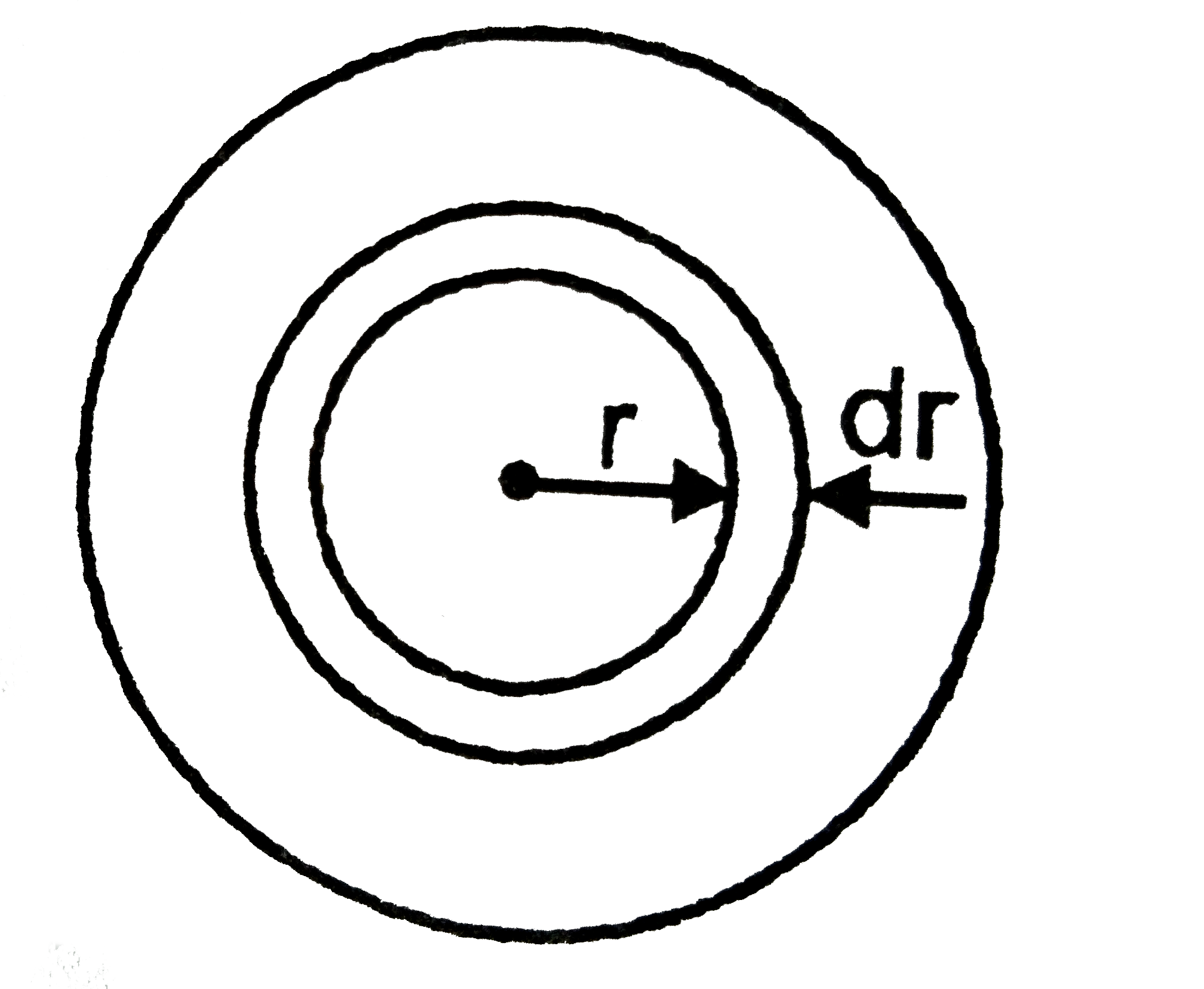
so
Electric field at a distance (r _1) from the center (inside )
.
Similar Questions
Let ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View Solution
Knowledge Check
Let ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQ4πε0r21BQr214πε0R4CQr213πε0R4DzeroLet p(r)=QπR4r be the charge JIR density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at distance z1from the centre of the sphere, the magnitude of electric field is
AQr214πε0R4BQr213πε0R4C0DQ4iε0r21Let ρ(r)=QrπR4 be the charge density distribution for a soild sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQ4πε0r21BQr214πε0R4CQr213πε0R4Dzero
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionLet p=Qr3πR5 be the volume charge density at distance r from the centre for a a soild sphere of radius R and charge Q. The electric field at r=R2 from the centre will be
View SolutionA sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View Solution