Three charges 0.1 coulomb each are placed on the corners of an equilateral triangle of side 1m. If the energy is supplied to this system at the rate of 1kW how much time would be required to move one ot the charges on to the midpoint of the line joining ther two ?
The correct Answer is:1.8×105sec
To solve the problem, we need to calculate the change in potential energy when one charge is moved to the midpoint of the line joining the other two charges, and then determine how long it would take to supply that energy at a rate of 1 kW.
1. Identify the Charges and Configuration:
We have three charges, each of 0.1C, placed at the corners of an equilateral triangle with a side length of 1m.
2. Calculate Initial Potential Energy:
The potential energy \( U_i \) of the system when all three charges are at the corners can be calculated using the formula for potential energy between point charges:
\(
U_i = k \left( \frac{q_1 q_2}{r_{12}} + \frac{q_1 q_3}{r_{13}} + \frac{q_2 q_3}{r_{23}} \right)
\)
Here, \( k = 9 \times 10^9 \, \text{N m}^2/\text{C}^2 \), \( q_1 = q_2 = q_3 = 0.1 \, C \), and \( r_{12} = r_{13} = r_{23} = 1 \, m \).
Thus,
\(
U_i = k \left( \frac{0.1 \times 0.1}{1} + \frac{0.1 \times 0.1}{1} + \frac{0.1 \times 0.1}{1} \right) = 3 \times k \times \frac{0.01}{1} = 3 \times 9 \times 10^9 \times 0.01 = 2.7 \times 10^8 \, J
\)
3. Calculate Final Potential Energy:
When one charge is moved to the midpoint of the line joining the other two charges, the distances change. The distance between the two charges remains 1m, but the distance from the midpoint to each charge is 0.5m.
The potential energy \( U_f \) in this new configuration is:
\(
U_f = k \left( \frac{q_1 q_2}{0.5} + \frac{q_1 q_3}{0.5} + \frac{q_2 q_3}{1} \right)
\)
\(
U_f = k \left( \frac{0.1 \times 0.1}{0.5} + \frac{0.1 \times 0.1}{0.5} + \frac{0.1 \times 0.1}{1} \right) = k \left( 2 \times \frac{0.01}{0.5} + \frac{0.01}{1} \right)
\)
\(
U_f = k \left( 2 \times 0.02 + 0.01 \right) = k \times 0.05 = 9 \times 10^9 \times 0.05 = 4.5 \times 10^8 \, J
\)
4. Calculate Change in Potential Energy:
The change in potential energy \( \Delta U \) is given by:
\(
\Delta U = U_f - U_i = 4.5 \times 10^8 - 2.7 \times 10^8 = 1.8 \times 10^8 \, J
\)
5. Calculate Time Required:
The energy is supplied at a rate of \( 1 \, kW = 1000 \, J/s \). The time \( t \) required to supply the energy \( \Delta U \) is:
\(
t = \frac{\Delta U}{\text{Power}} = \frac{1.8 \times 10^8}{1000} = 1.8 \times 10^5 \, s
\)
Final Answer:
The time required to move one of the charges to the midpoint of the line joining the other two is \( 1.8 \times 10^5 \, s \).
We have three charges, each of 0.1C, placed at the corners of an equilateral triangle with a side length of 1m.
The potential energy \( U_i \) of the system when all three charges are at the corners can be calculated using the formula for potential energy between point charges:
\(
U_i = k \left( \frac{q_1 q_2}{r_{12}} + \frac{q_1 q_3}{r_{13}} + \frac{q_2 q_3}{r_{23}} \right)
\)
Here, \( k = 9 \times 10^9 \, \text{N m}^2/\text{C}^2 \), \( q_1 = q_2 = q_3 = 0.1 \, C \), and \( r_{12} = r_{13} = r_{23} = 1 \, m \).
\(
U_i = k \left( \frac{0.1 \times 0.1}{1} + \frac{0.1 \times 0.1}{1} + \frac{0.1 \times 0.1}{1} \right) = 3 \times k \times \frac{0.01}{1} = 3 \times 9 \times 10^9 \times 0.01 = 2.7 \times 10^8 \, J
\)
When one charge is moved to the midpoint of the line joining the other two charges, the distances change. The distance between the two charges remains 1m, but the distance from the midpoint to each charge is 0.5m.
\(
U_f = k \left( \frac{q_1 q_2}{0.5} + \frac{q_1 q_3}{0.5} + \frac{q_2 q_3}{1} \right)
\)
\(
U_f = k \left( \frac{0.1 \times 0.1}{0.5} + \frac{0.1 \times 0.1}{0.5} + \frac{0.1 \times 0.1}{1} \right) = k \left( 2 \times \frac{0.01}{0.5} + \frac{0.01}{1} \right)
\)
\(
U_f = k \left( 2 \times 0.02 + 0.01 \right) = k \times 0.05 = 9 \times 10^9 \times 0.05 = 4.5 \times 10^8 \, J
\)
The change in potential energy \( \Delta U \) is given by:
\(
\Delta U = U_f - U_i = 4.5 \times 10^8 - 2.7 \times 10^8 = 1.8 \times 10^8 \, J
\)
The energy is supplied at a rate of \( 1 \, kW = 1000 \, J/s \). The time \( t \) required to supply the energy \( \Delta U \) is:
\(
t = \frac{\Delta U}{\text{Power}} = \frac{1.8 \times 10^8}{1000} = 1.8 \times 10^5 \, s
\)
The time required to move one of the charges to the midpoint of the line joining the other two is \( 1.8 \times 10^5 \, s \).
Similar Questions
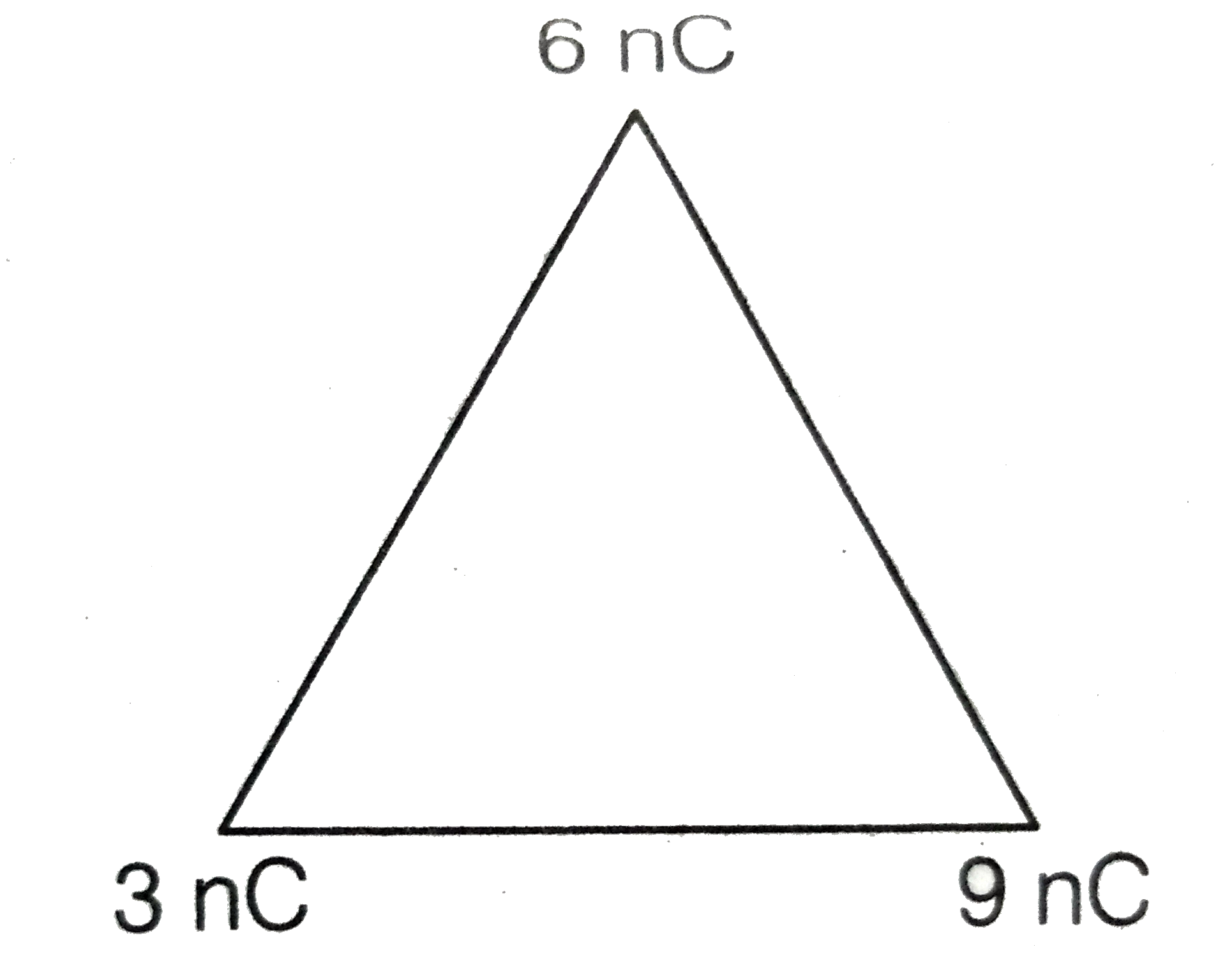
Three point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
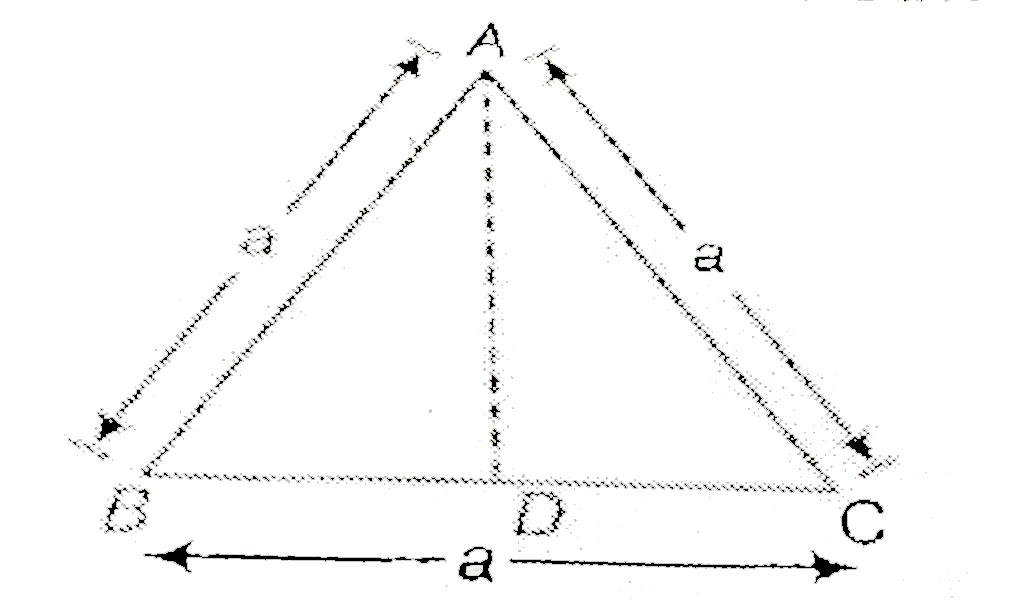
View SolutionAt the corners of an equilateral tringle of side a =1 m, three point charge are placed (each of 0.1 C). If this system is supplied energy at the rate of 1 kW, then calculate the time required to move one of charges to the mid-point of the line joining the other two.
View Solution
Knowledge Check
Three charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
A18×10−6JB9JC9×10−6JD27JThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A3GMa2B3GM2aC−3GM2a2D3GM2aAt the corners of an equilateral tringle of side a =1 m, three point charge are placed (each of 0.1 C). If this system is supplied energy at the rate of 1 kW, then calculate the time required to move one of charges to the mid-point of the line joining the other two.
 A50 hB60 hC48 hD54 h
A50 hB60 hC48 hD54 h
Three masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionThree point charges 2μC,3μCand5μC are placed at the corners of an equilateral triangle of side 200 cm. Calculate the potentail energy of the system.
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionCharges of +4μC,−6μCand−16μC are placed in air at the corners of an equilateral triangle of side 10. find the potential energy of the system. −0.72J
View SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View Solution

