A non-conductiong ring of radius −0.5m camies a total of 1.11×10−10C distributed non-unifrmly on its circumfernce producing an electric field →E every where in space . The value of the line integral ∫l=0t=∞−→E−→Ed→l(l=0) being centre of the ring ) in volts is -
+2
−1
−2
zero
The correct Answer is:A
Potential at the centre of ring =−∫l−0(l00)→E.−→Dl d
−∫l=0l=∞→E.→dl=KqR=2 volt.
Similar Questions
A charge of 4×10−9C is distributed uniformly over the circumference of a conducting ring of radius 0.3m. Calculate the field intensity at a point on the axis of the ring at 0.4m from its centre, and also at the centre.
View SolutionA ring of radius R=4m is made of a highly dense material. Mass of the ring is m1=5.4×109kg distributed uniformly over its circumference. A highly dense particle of mass m2=6×108kg is placed on the axis of the ring at a distance x0=3m from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
View Solution
Knowledge Check
A non-conducting ring of radius 0.5m carries a total charge of 1.11×10−10C distributed non-uniformly on its circumference producing an electric field E everywhere in space. The value of the integral ∫l=0l=∞−E.dl(l=0 being centre of the ring) in volt is
A+2B−1C−2DzeroA ring of radius 0.5m carries a total charge of 1.0×10−10C distributed non uniformly on its circum Ference, producting an electric field →E. The value of ∫r=0r=∞−→E.→dr(r=0 being the centre of the ring)is
A+1.8VB−6VC−1.8VD+6VSemicircular ring of radius 0.5 m is uniformly charged with a total charge of 1.4×10−9C. The electric field intensity at centre of this ring is :-
AzeroB320 V/mC64 V/mD32 V/m
A non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.
View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
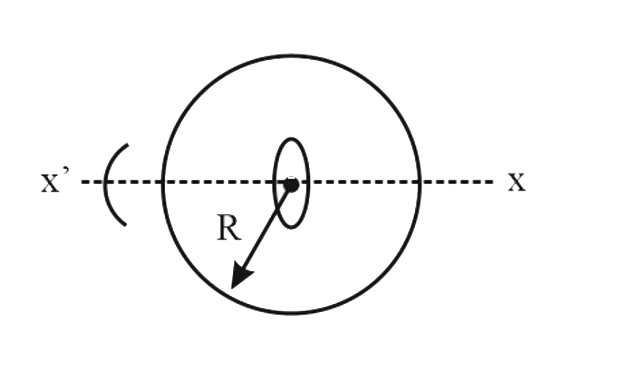
View SolutionA non-conducting ring of radius R having uniformly distributed charge Q starts rotating about x-x' axis passing through diameter with an angular acceleration α, as shown in the figure. Another small conducting ring having radius a(a<<R) is kept fixed at the centre of bigger ring is such a way that axis xx' is passing through its centre and perpendicular to its plane. If the resistance of small ring is r=1Ω , find the induced current in it in ampere.
(Given q=16×102μ0C,R=1m,a=0.1m,α=8rad s−2
View SolutionA semicircular ring of radius 0.5 m is uniformly charged with a total charge of 1.5×10−9 coul. The electric potential at the centre of this ring is :
View SolutionThere is a non conducting ring of radius R and mass m having charge q uniformly distributed over its circumference. It is placed on a rough horizontal surface. A vertical time varying uniform magnetic field B=4t2 is switched on at time t= 0. The coefficient of friction between the ring and the table, if the ring starts rotating at t= 1 sec, is :
View Solution
