Question

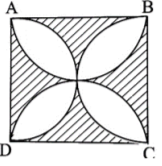
In the given figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region. Use $\pi =\frac{22}{7}$.

Explanation

In the given figure, ABCD is a square with side 14 cm. It has semi-circles drawn with its sides as diameter.
To find, the area of the shaded region we first need to find area of square `= s^2`
`= 14^2 = 196 cm^2`
Radius of semi circles = half of side of square = `14/2 = 7 cm`
area of 1 semi-circle `= (pi*r^2)/2`
area of 4 semi-circles `= 4*(pi*r^2)/2 = (4*pi*7^2)/2 = 22*7*2 = 308 cm^2`
Area of semi-circles - area of square = area of unshaded region `= 308 - 196 = 112`
Area of shaded region = Area of square - area of unshaded region `= 196 - 112 = 84 cm^2`